Математическая модель амбивалентных систем с переменными коэффициентами

.

.

.

.

.

.

.

Анализ устойчивости амбивалентных систем при различных коэффициентах равновесия

Как было показано в разделе 2.1, зависимость вероятностей состояний от коэффициента равновесия k носит нелинейный характер и качественно различается при k =1 и при k >>1.

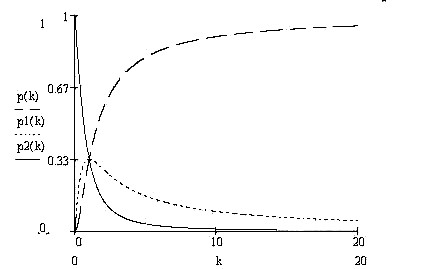
Из рисунка видно, что состояние гомеостаза разное в точке и в точке . Визуально видно, что при k =1 зона устойчивого гомеостаза небольшая, в отличие от точки k =20, где диапазон его изменения большой. Предлагается первый случай назвать “мягкий” гомеостаз, а второй “жесткий”. Исследуем это аналитически. Введем некоторый интервал , внутри которого будет сохраняться состояние гомеостаза в точке и в точке . Ставится задача найти диапазон изменения коэффициента , при котором сохраняется гомеостаз.

1) Для точки , имеем уравнение для смеси:

Получаем квадратное уравнение:

, или

или

,

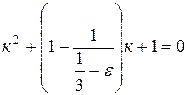После преобразования получим конечное уравнение:

,

где ,

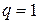
Находим дискриминант:

При 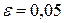, , 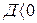соответственно имеем два корня

В общем случае область устойчивости гомеостаза в точке равна:

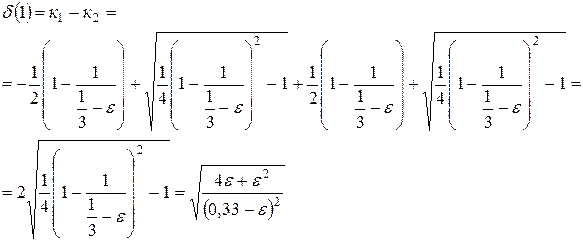
при , .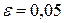

2) В точке

После преобразования получаем квадратное уравнение:

,

отсюда

,

где , .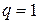

Дискриминант , при , ,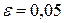

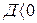Здесь представляет интерес корень, близкий к 20,

,

т.к. второй корень значительно больше 20 и, можно считать его равным бесконечности. Тогда диапазон устойчивости гомеостаза для 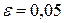равен . Найдем крайние значения коэффициента , при которых сохраняется гомеостаз.

,

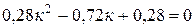
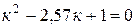
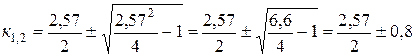
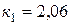График зависимости зоны устойчивости для гомеостаза λ=µ («мягкий» гомеостаз) и 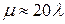(« жесткий» гомеостаз ) имеет следующий вид:

	Жесткий гомеостаз
		Мягкий гомеостаз

Рис.2.11

Всегда ли состояние гомеостаза является эффективным с точки зрения пользователя системы? В работе [11] при анализе химического процесса получения хлорноватистой кислоты было показано, что в этом состоянии наблюдается малый выход продукта и, следовательно, возникает проблема смещения гомеостаза для увеличения эффективности работы системы.

В амбивалентных системах смещение гомеостаза легко осуществляется путем усиления влияния той или иной противоположности. В бестселлере 21 века [9] рассказывается о методе лечения болезней человека, рассматриваемого как сочетание двух противоположностей Ян и Инь: Ян и Инь – это две взаимодополняющие противоположности, присутствующие в каждом явлении. Согласно восточным представлениям, при нарушении равновесия этих противоположностей в живом организме можно говорить о его патологическом состоянии.

Одним из принципов лечения является правило «БУ - СЕ», которое означает: прибавить «БУ» - отнять «СЕ». Врачи, применяя на практике эти принципы, широко используют биологически активные добавки, несущие в себе эти противоположности. В состав продуктов «Инь» входят арбуз, виноград, вода, соль, яйцо, морковка, свинина и т.д. В состав продуктов «Ян» входят: кукуруза, горчица, прополис, мука, вино, говядина, баранина, грецкий орех и т.д.

Летом, в жару, рекомендуется кушать больше «иньской», охлаждающей пищи. Зимой же предпочтение следует отдавать согревающей «янской».

По - существу, этот же принцип был использован при управлении технологическим процессом для увеличения выхода хлорноватистой кислоты путем удаления части соляной кислоты [12]. В ответ на удаление соляной кислоты из реакционной зоны, гомеостатическая система стремится восстановить недостаток соляной кислоты и снова выйти на состояние равновесия.

В ходе проведенных исследований по смещению равновесия удалось получить численные данные о характере зависимости между величиной смещения и выходом готового продукта. Эта зависимость имеет ограниченный линейный участок, который при больших значениях смещения переходит в нелинейный и обрывается. Это происходит из за того, что образуется щелочная среда и выход хлорноватистой кислоты уменьшается: т.е. технологический процесс находился в состоянии «тонкого» гомеостаза с небольшим запасом устойчивости.

Очевидно, такое явление можно объяснить исчерпанием запаса устойчивости и не здесь ли лежит объяснение гомеопатическим методам лечения ряда болезней человека (лечение малыми дозами). С другой стороны необходимо знать в каком состоянии гомеостаза проводится лечение: когда запаса устойчивости мало или когда оно очень большое; в медицинской практике известны случаи положительных результатов при больших дозах воздействия на организм, например, электрошок при реанимации сердечной деятельности.

На основании всего вышесказанного делается вывод о том, что при управлении в амбивалентных системах необходимо учитывать в каком гомеостазе находится система: в «мягком» или «жестком» и в соответствии с этим принимать решения о величине смешения. Такой вывод особенно актуален для социальных систем, где руководителю постоянно необходимо принимать решения о создании в коллективе дружественных отношений, как тут не вспомнить замечательные слова из песни В.Высоцкого:

Если друг оказался вдруг

И не друг, и не враг, а – так,

Если сразу не разберешь,

Плох он или хорош,-

Парня в горы тяни - рискни!

Не бросай одного его!

Пусть он в связке одной с тобой-

Там поймешь, кто такой.

2.1.3. Динамика амбивалентных систем

Сделаем анализ перехода амбивалентной системы из начального состояния в состояние гомеостаза и сравним время перехода в разные гомеостазы.

Решение дифференциальных уравнений Колмогорова, описывающих поведение амбивалентной системы с параметрами и , в явном виде при начальных условиях P₀(0)=1, P₁(0)=0, P₂(0)=0 выглядит следующим образом [13]:

;

;

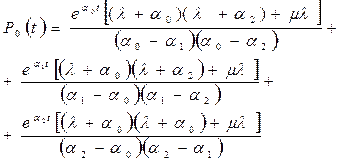Для начальных условий выглядит следующим образом:

Для начальных условий :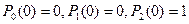

где , , 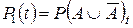, , , 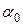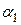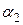-корни характеристического уравнения, детерминант которого имеет следующий вид и равен 0.

Решая это уравнение, находим, что

Корень 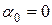определяет стационарный режим работы системы при .

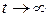Рассмотрим переход системы в состояние “мягкого” гомеостаза при , т.е. . В этом случае , , 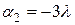. Подставляя значение корней в уравнение имеем:

При 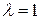, задаваясь порогом 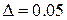получаем:

для состояния 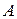: , t=2.31 ед. времени;

для состояния : , , ;

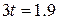для состояния : , ед. времени.

Т.е. подтверждается вывод о том, что переход в стационарный режим для состояния смеси происходит раньше, чем в состояния 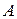и .

Исследуем время перехода в состояние «жесткого» гомеостаза, когда m >> l, например, m=10l:

,

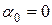a₁=-7.8l

P₀ (t) = 0,9+0,06e ^{–7,8l t} +0,04e ^{–14,16l t}

P₁ (t) = 0,09+0,043e ^{–7,8l t} -0,048e ^{–14,16l t}

P₂ (t) = 0,009+0,02e ^{–7,8l t} +0,011e ^{–14,16l t}

При 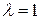и величине порога 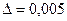имеем

для : , ,

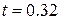для : , ,

для : , .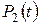

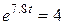То есть подтверждается вывод о том, что время перехода в этом случае имеет разное значение для стационарных режимов.

Для более наглядного изучения зависимости вероятностей состояний АС от параметра λ и времени t были построены трехмерные графики

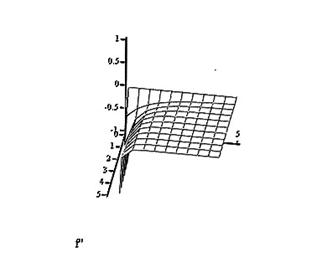
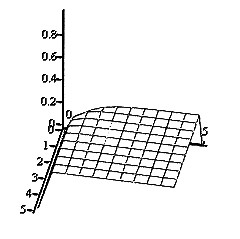
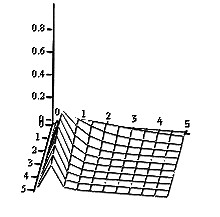
Приведенные графики показывают, что при больших значениях времени функционирования t(больше времени переходного режима) вероятности состояний мало зависят от параметров λ и μ.

Исследуем более подробно влияние отдельных параметров lи mна вероятности состояний в амбивалентных системах для «мягкого» и «жесткого» гомеостаза.

«Мягкий» гомеостаз.

Возьмем производную по параметру λ.

Ниже на рисунке 2.12 приведены графики зависимости производных для трех состояний от λ при t =0,13.

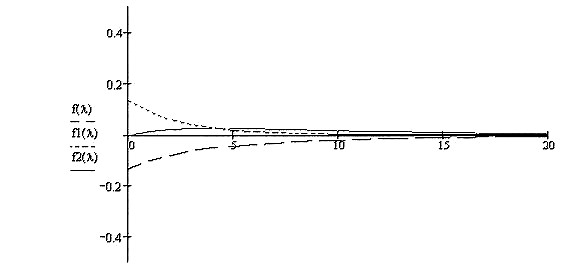
Рис.2.12

Из графика видно, что в состоянии «мягкого» гомеостаза, когда , длямалых значений времени функционирования, вероятности состояний амбивалентной системы зависят от параметра λ. Причем, чем больше этот параметр, тем меньше зависимость.

Исследуем зависимость от параметра λ при больших значениях времени функционирования t = 5,0. На рис.2.13 показаны такие зависимости для всех трех состояний системы.

Рис.2.13

Из графика видно, что в состоянии “мягкого” гомеостаза, когда при больших значениях времени функционирования вероятности состояний не зависят от величины параметра , когда >=1.

«Жесткий» гомеостаз.

Возьмем производную по параметру l

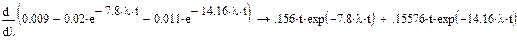
Для времени функционирования амбивалентных систем равной t =0,13 на рис. 2.14 показаны графики зависимости вероятностей состояний от λ.

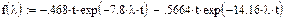
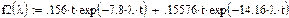
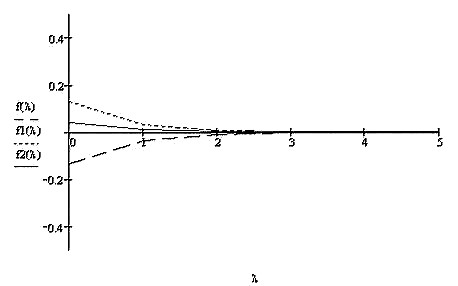
Рис.2.14

Видно, что в режиме «жесткого» гомеостаза при малых значениях времени функционирования эти вероятности зависят по-разному в зависимости от величины λ: при малых значениях λ есть зависимость, а при λ ≥ 3 такой зависимости нет.

Также было проведено исследование поведения системы в этом режиме при больших временах функционирования системы и на рисунке 2.15 приведены графики соответствующих зависимостей.

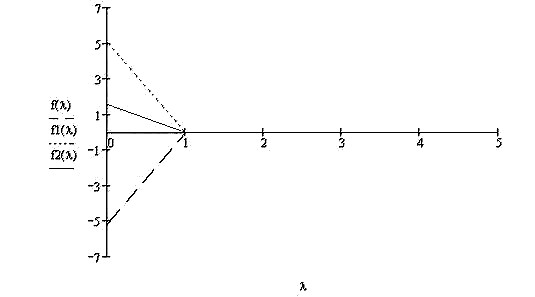
Рис.2.15

Из приведенных графиков зависимости производной вероятностей состояний амбивалентных систем от параметра в режиме «жесткого» гомеостаза при больших значениях времени функционирования видно, что вероятности состояний не зависят от величины для значительно больше единицы.

Исследуем поведение амбивалентной системы во времени при различных комбинациях значений параметров этих систем в режимах «мягкого» и «жесткого» гомеостаза и начальных состояний.

Вариант 1. «Мягкий» гомеостаз: λ=1 µ=1.

Рис.2.16

На рис.2.16 показан график зависимости вероятностей состояний амбивалентной системы для «мягкого» гомеостаза, когда эта система в начальный момент времени находится в состоянии А.

Из графика видно, что время перехода в состояние смеси меньше, чем в другие состояния.

Вариант 2. «Мягкий» гомеостаз: λ=1 µ=1.

Рис.2.17

На рис.2.17 показан график зависимости вероятностей состояний амбивалентной системы для «мягкого» гомеостаза, когда эта система в начальный момент времени находится в состоянии .

Из графика видно, что время перехода в стационарный режим, когда вероятности всех состояний равны между собой, одинаково для всех состояний.

Вариант 3. «Мягкий» гомеостаз: λ=1 µ=1.

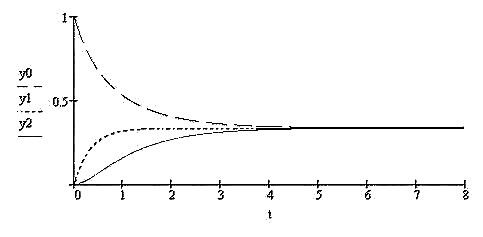
Рис.2.18

На рис.2.18 показан график зависимости вероятностей состояний амбивалентной системы для установившегося режима («мягкого» гомеостаза) в точке равновесия, когда эта система в начальный момент времени находится в состоянии . Из графика видно, что время перехода в состояние смеси меньше, чем в другие состояния.

Вариант 4.«Жесткий» гомеостаз: λ=1
µ=10.

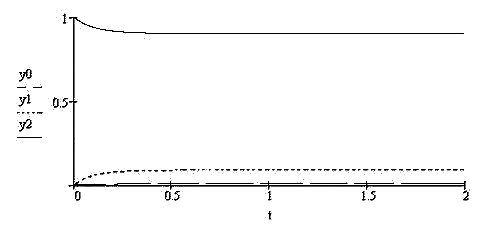
Рис.2.19

На рис.2.19 показан график зависимости вероятностей состояний от времени для амбивалентной системы, когда эта система находится во втором установившемся гомеостатическом режиме («жесткий» гомеостаз). Из графика видно, что амбивалентная система приходит в этот установившейся режим практически одновременно для всех трех состояний. Обращает на себя внимание тот факт, что вероятность состояния остается весьма незначительной, а вероятность смеси возрастает, но также незначительно.

Вариант 5. «Жесткий» гомеостаз: λ=1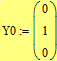
µ=10.

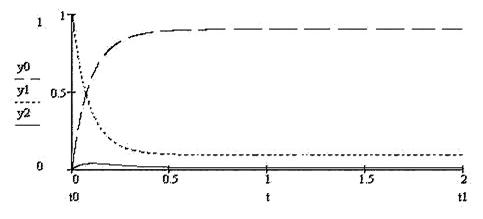
Рис.2.20

На рис.2.20 показан график зависимости вероятностей состояний от времени для амбивалентной системы, когда эта система находится во втором установившемся гомеостатическом режиме. Из графика видно, что такая система приходит в установившийся режим практически одновременно для всех трех состояний. Обращает на себя внимание тот факт, что вероятность состояния остается весьма незначительной.

Вариант 6. «Жесткий» гомеостаз: λ=1 µ=10.

Рис.2.21

На рис.2.21 показан график зависимости вероятностей состояний от времени для амбивалентной системы, когда эта система находится во втором установившемся гомеостатическом режиме («жесткий» гомеостаз). Из графика видно, что такая система приходит в установившийся режим практически одновременно для всех трех состояний.

Вариант 7. «Жесткий» гомеостаз: λ=10 µ=1.

Рис.2.22

Из графика рис.2.22 видно, что этот вариант аналогичен варианту 6.

Вариант 8. «Жесткий» гомеостаз: λ=10 µ=1.

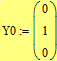
Рис.2.23

Из графика рис.2.23 видно, что этот вариант аналогичен варианту 5. Полученные результаты подтверждают вывод о том, что влияние параметровλ и µ на процессы, происходящие в амбивалентных системах одинаково.

Вариант 9. «Жесткий» гомеостаз: λ=10 µ=1.

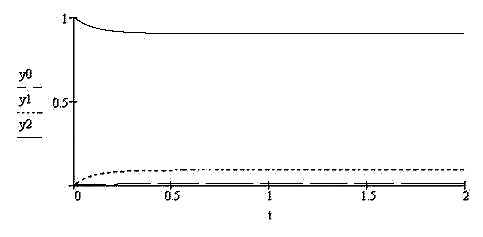
Рис.2.24

Из графика на рис.2.24 видно, что этот вариант аналогичен варианту 4 с тем отличием, что все интерпретируется по отношению к состоянию .

Представляет большой интерес исследование поведение амбивалентной системы, когда параметры системы l и m являются не постоянными, а переменными во времени величинами и более того, связаны с вероятностями состояний системы. Здесь, очевидно, возможны два варианта работы системы: прямо пропорциональная зависимость и обратно пропорциональная.

Рассмотрим вариант работы системы, когда интенсивности перехода пропорциональны вероятностям состояний. Этот случай представляет несомненный практический интерес. Не ограничивая общности рассмотрения, можно при исследовании считать равным единице коэффициент пропорциональности, тогда 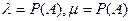и система дифференциальных уравнений, описывающая этот случай становится нелинейной:

l= P (A), m= P(Ā),

P¢(A)_t = - P ²(A) _t + P(A) _t P(Ā) _t,

P¢(A Ú Ā)_t = P ²(A) _t – [ P (A) _t + P (Ā) _t ] P (A Ú Ā) _t + P ²(Ā) _t

P¢(Ā)_t = - P ²(Ā) _t + P (A) _t P (A Ú Ā) _t

P(A) _t + P (A Ú Ā) _t + P(Ā) _t = 1, P (A) ₀ = 1

На рис.2.25 показано решение данной нелинейной системы.

Рис. 2.25

Как видно из рисунка такая система также приходит в состояние равновесия, когда P(A)= P(Ā)= P(A Ú Ā)= 0,333, но состояние смеси устанавливается раньше других, причем через точку перегиба: действительно, при t = 1,5 P(A Ú Ā)= 0,35, а затем уже при t= 7 P(A Ú Ā)= 0.333.

Исследуем поведение данной системы на устойчивость. По аналогии с вариантом системы с постоянными коэффициентами, задаём приращение в точке равновесия

С учётом нормировочного условия получаем, что

поэтому достаточно рассмотреть только изменения для и .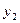

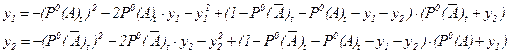
Для анализа устойчивости, достаточно линеаризовать полученные уравнения, осуществляя одновременно параллельный перенос

Находим собственные значения матрицы системы для осуществления ортогонального преобразования

Аналогично линейному случаю с учётом поворота оси координат

и система не устойчива, если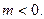

Очевидно, что 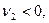предполагаем, что тогда должно выполниться:

или

,

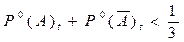и, согласно нормировочному условию,

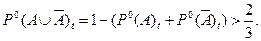
Значит положение, при котором

, а

неустойчиво. При

бинарная система устойчива.

Первый вариант исследования поведения данной системы иллюстрирует принцип мирного сосуществования двух противоположностей.

Был проведен анализ второго варианта нелинейной системы с противоположностями, когда интенсивности перехода обратно пропорциональны вероятностям состояний:

l= 1/P (A)_t , m= 1/P(Ā)_t,

P¢(A)_t = -1 + P(A Ú Ā)_t/P(Ā)_t,

P(A Ú Ā)_t = 2 – (1/P(A)_t + 1/P(Ā)_t ) P(A Ú Ā)_t ,

P¢(Ā)_t = -1 + P(Ā)_t / P (A)_t ,

P(A) ₀ = P (A Ú Ā) ₀ = 0.3 P(Ā) ₀ = 0.4

На рис. 2.26 показаны результаты решения задачи. Система является неустойчивой и уже при малых значениях времени функционирования (t£ 0,5) процесс расходится.

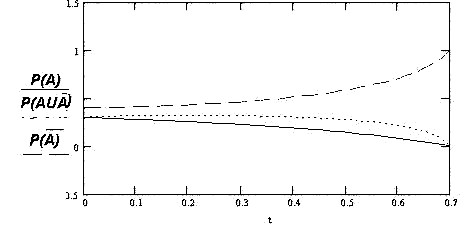
Рис. 2.26

Из рис.2.26 видно, что со временем начинает преобладать та противоположность, которая в начальный момент времени имеет большее значение:

при t=0 P(Ā)=0.4, тогда как P(A)= P(A Ú Ā)= 0.333

и уже при t=0,7 P(Ā)=1.

Второй вариант иллюстрирует поведение амбивалентной системы с противоречиями, носящими антагонистический характер, когда одна противоположность существенно подавляет другую.

Дата добавления: 2014-12-16