В образовании. Амбивалентная система обучения неродному языку

.

На рис.2.4 эта зависимость показана сплошной линией. Можно высказать предположение, что наличие смеси в системе это, как - бы, результат того, что острота противоречия минимальна. Смешанные браки между разными народами могут быть только на основе дружбы, наличие безразличия между членами коллектива не вызывает каких - либо конфликтов, то - есть, чем выше уровень смеси, тем меньше острота противоречия и, наоборот, чем меньше уровень смеси, тем выше острота противоречия.

Если, также как в первом варианте принять условие, что при k=1 острота противоречия равна нулю, то зависимость ее от параметра k, выраженная в процентах, имеет следующий вид

.

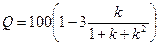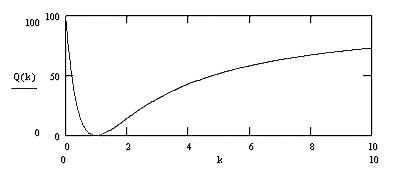
рис.2.36

На рис.2.36 показан график этой зависимости, из которого видно, что с увеличением параметра kв отличие от первого варианта нет резкого возрастания остроты противоречия до 100 процентов. Это объясняется тем, что при больших значениях k, какой то отличный от нуля уровень смеси остается и, следовательно, напряженность между противоположностями ослабляется. При втором варианте можно непосредственно измерять остроту противоречия через вероятность наличия смеси по формуле:

Q= 100-300 P(A Ú Ā),

где P(A Ú Ā) изменяетсяот 0 до 1/3.

Практическое применение предлагаемых в статье формул, в частности по первому варианту, для оценки остроты противоречия может вызвать определенные трудности, так как измерять интенсивности переходов между противоположностями (λ и µ) можно только в технических системах, например, в химических системах с прямой и обратной реакцией, как правило, скорости этих реакций известны. Для социальных систем таких возможностей нет, автор, к сожалению, не может рекомендовать способ измерения интенсивности перехода от любви к ненависти и обратно, от антипатии к симпатии и обратно и т.д.

Второй вариант оценки остроты противоречия кажется более предпочтительным, так как измерять уровень смеси в амбивалентных системах, как в технических, так и в социальных можно по статистическим данным.

Так, например, оценивать напряженность в смешанных браках можно по количеству браков и разводов между черными и белыми, украинцами и русскими, грузинами и армянами и т.д. Степень социальной напряженности в обществе можно измерять по величине среднего класса, степень остроты противоречия в семейных отношениях измерять по количеству заключаемых браков и разводов между молодыми людьми и т.д.

Предложенные формулы для оценки противоречия позволяют поставить обратную задачу вычисления параметра kпри заданном значении Q. Здесь можно привести следующие рассуждения: если требуется, чтобы острота противоречия была равна нулю, то необходимо иметь значение kравным единице, но в этом случае, как было показано выше, имеет место «мягкий» гомеостаз, в котором система работает не эффективно и для увеличения эффективности необходимо смещать точку равновесия. Этот вывод был сделан для химической реакции, но он, очевидно, может быть обобщен и на другие системы на основании применения принципа Ле-Шателье.

При Q 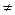0, задаваясь конкретным численным значением Q, по предложенным формулам вычисляем либо параметр k, либо уровень смеси, соответствующий данной оценке противоречия. Например, для Q= 50% по линейной формуле получаем k= 0,5 или k= 5,5, для второго варианта по нелинейной зависимости уровень смеси P(A Ú Ā) = 0,17.

В качестве подтверждения того, что обратная задача нахождения соответствующего компромисса между противоположностями реальна, приведем результаты исследований британских ученых, которые разработали математическую модель настоящей и вечной любви. По их утверждению, эти расчеты позволяют установить, долго ли продлятся отношения пары с точностью до 94%. Участникам исследований предлагалось в течении 15 минут поговорить на темы, по которым пары имеют противоположные мнения: деньги, секс, политика, отношения с родителями и т.д. После беседы составлялся график пересечения ответов жены и мужа. Чем чаще пересекались линии, тем больше шансов на успех было у этого брака, иные результаты свидетельствовали о скором разводе. Очевидно, что неплохо было бы эту формулу применять ещё до вступления в брак, тогда количество разводов было бы значительно меньше.

Глава 3. Применение теории амбивалентных систем

Функции коры головного мозга, по мнению Goertyel B. [18], являются непредсказуемыми на уровне деталей, но грубо предсказуемыми на уровне структуры. Явление субординативного билингвизма тесно связано с интерязыком, промежуточной самосозидающейся и саморазвивающейся лингвистической системой.

Таким образом, нами рассматриваются две лингвистические системы: родной язык и неродной язык. В результате изучения неродного языка возникает третья лингвистическая система – интерязык. Схема взаимодействия родного и неродного языков в процессе обучения согласно представлениям лингвистов выглядит следующим образом [19]: из 100% обучающихся 5% достигают координативного (совершенного) билингвизма, при котором билинг в совершенстве владеет как родным, так и иностранным языками. Остальные 95% достигают состояния субординативного билингвизма, при котором наблюдаются постоянные динамические процессы либо в сторону увеличения объема знаний и сужению системы интерязыка, либо в сторону «отката знаний» и увеличению системы интерязыка отмирания из-за невостребованности. Также наблюдается третий режим, режим «окостенения», когда объем знаний интерязыка фиксирован и находится без изменения.

Процесс обучения в такой системе можно рассматривать как процесс взаимодействия двух противоположностей, в котором одна противоположность переходит в другую и обратно, такие системы называются амбивалентными системами, поведение которых можно анализировать на основе предложенных выше математических моделей.

Графически процесс взаимодействия родного и неродного языков можно представить в виде следующей схемы.

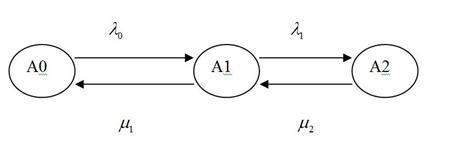
Рис.3.1

На рис.3.1 показан граф модели субординативного билингвизма, как амбивалентная система, где А0 - состояние родного языка, А1 - состояние интерязыка, А2 - состояние неродного языка,

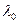
- интенсивность использования родного языка для изучения неродного языка,

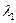- интенсивность обращения к неродному языку в процессе его изучения (очевидно, что этот параметр можно также связывать с процессом забывания),

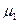- интенсивность обращения к родному языку при забывании значений слов, выражений, понятий неродного языка (явление «отката» из интерязыка),

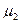- интенсивность использования неродного языка в процессе его изучения.

С точки зрения амбивалентных систем параметр характеризует преобразование родного языка в неродной, а параметр процесс обратного преобразования.

Предполагается, что процесс изучения неродного языка носит вероятностный характер, так как зависит от множества часто случайных факторов. С учетом этого предположения в качестве математической модели для анализа субординативного билингвизма предлагается следующая система дифференциальных уравнений, записанная относительно вероятностей состояний:

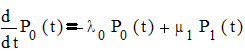
Матрица переходов выглядит следующим образом:

.

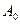
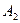
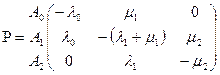Предполагаем, что начальное состояние билинга А0, т.е. Р 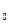(0) = 1, Р 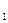(0) = Р 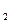(0) = 0.

Решение такой системы дифференциальных уравнений известно и в общем случае имеет следующий вид [13]:

,

,

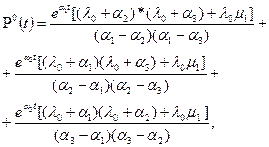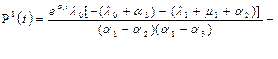
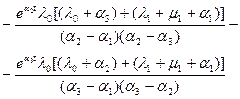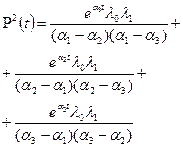, (1)

где ,

,

,

, , ,

,

.

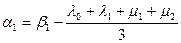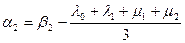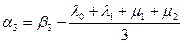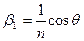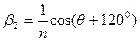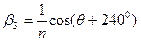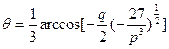
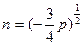
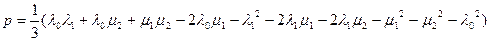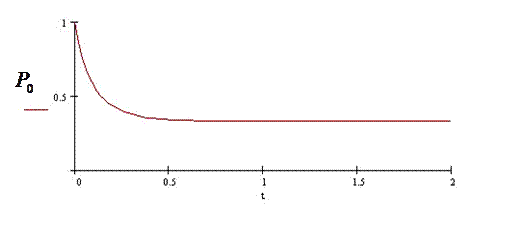
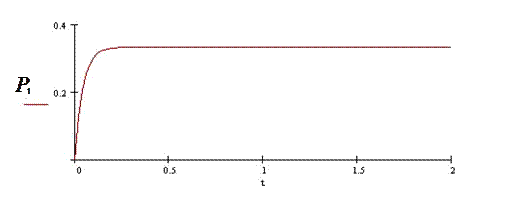
Предложенная математическая модель показывает зависимость поведения системы от четырех параметров. На рис.3.2 показаны графики, показывающие зависимости вероятностей состояний системы от этих параметров по времени, содержательная интерпретация которых и представляет интерес.

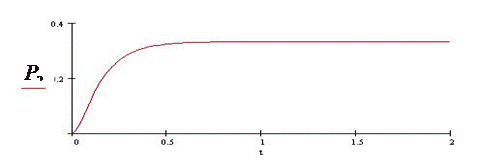
Рис.3.2.

График рис.3.2 показывает зависимость вероятностей состояний родного языка P₀, интерязыка P₁ и неродного языка P₂ от времени при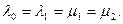

Во-первых, обращает на себя внимание тот факт, что по истечении некоторого времени процесс обучения переходит в установившейся режим, при котором вероятности состояний не меняются (такой режим можно, очевидно, назвать режимом «окостенения»). Для такого режима система дифференциальных уравнений, описывающих процесс обучения, переходит в систему алгебраических уравнений следующего вида:

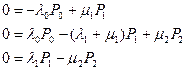
С учетом того, что 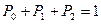находим решение данной системы, которое имеет следующий вид:

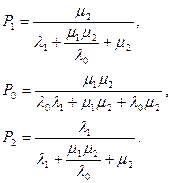
Обращает на себя внимание тот факт, что при равенстве всех четырех параметров между собой вероятности трех состояний также равны и равны 1/3, т.е. идет интенсивное формирование интерязыка, как смеси родного и неродного языков.

В качестве примера формирования режима «отката», на рис.3.3 приведен график зависимости вероятности состояния интерязыка, полученный при других соотношениях между параметрами процесса обучения (интенсивностями обращения к родному и неродному языкам).

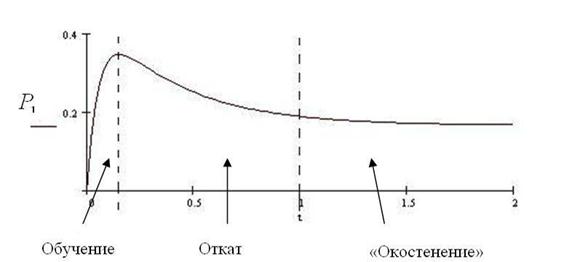
Рис.3.3

На приведенном графике показана зависимость вероятности состояния интерязыка P₁ от времени при неравенстве параметров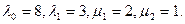

Действительно, как показывает график для P₁, сначала идет интенсивное формирование интерязыка, а затем появляется спад, причина которого, скорее всего связана с малой интенсивностью обращения к неродному языку. Модель субординативного билингвизма показывает, что процесс отмирания не доходит до нуля и при достаточно большом времени функционирования все-таки имеют место остаточные знания неродного языка.

Одно из интересных применений модели связано с тем, что можно в процессе обучения менять параметры модели и наблюдать поведение учащегося при этом: если нас не устраивает получившийся объем знаний интерязыка, то следует изменить параметры для такого учащегося в нужную для преподавателя сторону.

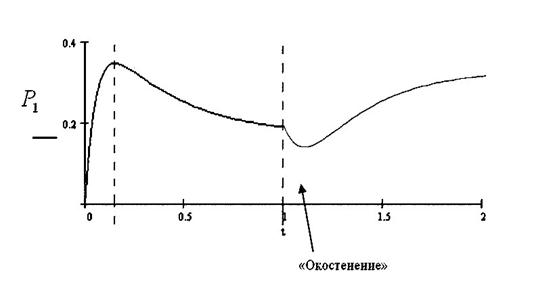
Рис.3.4

Изменение процесса обучения в режиме «окостенение» при изменении параметров обучения показано на рисунке 3.4, из которого видно, что после момента времени t=1 происходит изменение хода обучения при изменении параметров модели λ и µ и, следовательно, самого ходаобучения в лучшую сторону.

Другое применение модели субординативного билингвизма связано с тем, что на ее основе можно предложить оригинальную технологию обучения неродному языку с учетом индивидуальных особенностей учащегося, и в первую очередь, конечно, его начальных знаний неродного языка, которые могут быть введены при решении дифференциальных уравнений в виде начальных состояний. Конкретные особенности каждого учащегося, а именно его способности к запоминанию и забыванию иностранных слов могут быть введены в модель в виде параметров модели, здесь, конечно, возникает проблема определения параметров индивидуальной модели путем статистической обработки трека обучения для конкретногообучаемого.

Определив на основе тестирования начальный уровень знаний неродного языка каждого обучаемого и нормативные параметры модели образования его интерязыка, по математической модели прогнозируется индивидуальный трек обучаемого. На стадии обучения ведут контроль за формированием реального уровня интерязыка обучаемого, сравнивая его с расчетным.

В случае обнаружения снижения уровня усвоения неродного языка и увеличения корпуса интерязыка, вводят скорректированные параметры модели интерязыка и рассчитывают трек обучаемого и уровень владения неродным языком. На основе этого предлагают откорректированный режим обучения конкретного учащегося, что предусматривает первоначально спрогнозированный уровень знаний. Если обнаруживаются отклонения от заданного трека, то усиливают интенсивность процесса обучения и обращаются к модели образования интерязыка для повторного прогнозирования, индивидуального трека обучаемого и ведут сравнение с расчетным.

3.2. Моделирование химико-технологических процессов с противоположностями

В данном разделе даются методологические и математические основы исследования ряда химико-технологических процессов, в которых, по мнению автора, работает закон единства и борьбы противоположностей. Вначале дается описание химико-технологических процессов с противоположностями. Все материалы данного раздела взяты из кандидатской диссертации Сенотовой С.А., руководителем которой являлся автор данной монографии [20].

Дата добавления: 2014-12-16