
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Механические колебания
|
|
|
|
ЗАДАНИЕ № 37
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и частотой ν= 2 Гц. Если смещение точки в момент времени, принятый за начальный, равен своему максимальному значению, то точка колеблется в соответствии с уравнением …
ВАРИАНТЫ ОТВЕТОВ:
1) x= 0,04cos πt;3) x= 0,04cos(π/2) t;5) x= 0,04cos 4πt;
2) x= 0,04sin πt;4) x= 0,04sin(π/2) t;6) x= 0,04sin 4πt.
ЗАДАНИЕ № 38
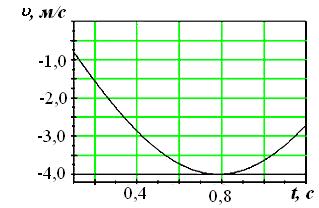
На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону.
|
Циклическая частота колебаний точки равна …
1) 1 с-1 ; 2) 2 с-1; 3) 3 с-1; 4) 4 с-1.
ЗАДАНИЕ № 39
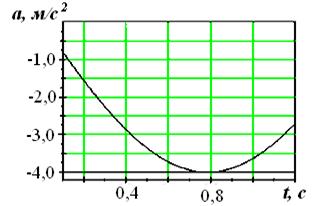
На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону.
|
Циклическая частота колебаний точки равна …
1) 1 с-1 ; 2) 2 с-1; 3) 3 с-1; 4) 4 с-1.
ЗАДАНИЕ № 40
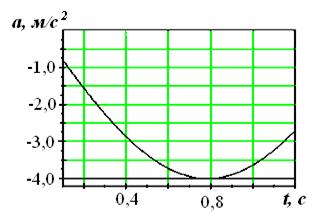
На рисунках изображены зависимости от времени скорости и ускорения материальной точки, колеблющейся по гармоническому закону.
|
Циклическая частота колебаний точки равна …
1) 1 с-1 ; 2) 2 с-1; 3) 3 с-1; 4) 4 с-1.
ЗАДАНИЕ № 41
Частица может колебаться вдоль оси x под действием результирующей силы  с амплитудой А и частотой w, где k – положительная константа. В момент, когда x=А/ 2, скорость частицы будет равна:
с амплитудой А и частотой w, где k – положительная константа. В момент, когда x=А/ 2, скорость частицы будет равна:
ВАРИАНТЫ ОТВЕТОВ:
1)  ; 2)
; 2) 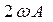 ; 3)
; 3)  ;
;
4) 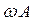 ; 5)
; 5)  .
.
---------------------------
Указания к заданиям №№ 37 – 41
Гармонические колебания величины  (координаты материальной точки) описываются уравнением:
(координаты материальной точки) описываются уравнением:
 , где
, где
А – амплитуда колебаний – максимальное значение колеблющейся величины;
ω0 – круговая (циклическая) частота;
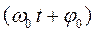 – фаза колебаний в момент времени t;
– фаза колебаний в момент времени t;
j0 – начальная фаза колебаний.
Скорость материальной точки:  .
.
Ускорение материальной точки:  .
.
Максимальные значения смещения x, скорости u, ускорения a:

ЗАДАНИЕ № 42
Частица массы m, движущаяся вдоль оси x, имеет потенциальную энергию U(x)=a+bx2, где a и b – положительные константы. Начальная скорость частицы равна V0 в точке x= 0. Частица совершает гармонические колебания с частотой, определяемой значениями:
ВАРИАНТЫ ОТВЕТОВ:
1) только b и m;
2) только b и a;
3) b, a, m и V0;
4) только b, a и m;
5) только b.
---------------------------
Указание
Круговая частота гармонического колебания частицы массой m вдоль оси х:
 , где k – коэффициент упругости в соотношении
, где k – коэффициент упругости в соотношении 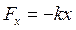
(Fx – возвращающая сила:  , где U(x) – потенциальная энергия).
, где U(x) – потенциальная энергия).
ЗАДАНИЕ № 43
Уравнение пружинного маятника 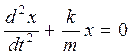 является дифференциальным уравнением …
является дифференциальным уравнением …
ВАРИАНТЫ ОТВЕТОВ:
1) cвободных незатухающих колебаний;
2) cвободных затухающих колебаний;
3) вынужденных колебаний.
ЗАДАНИЕ № 44
Уравнение пружинного маятника  является дифференциальным уравнением…
является дифференциальным уравнением…
ВАРИАНТЫ ОТВЕТОВ:
1) свободных незатухающих колебаний;
2) свободных затухающих колебаний;
3) вынужденных колебаний.
ЗАДАНИЕ № 45
Уравнение пружинного маятника 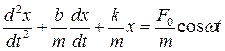 является дифференциальным уравнением…
является дифференциальным уравнением…
ВАРИАНТЫ ОТВЕТОВ:
1) свободных незатухающих колебаний;
2) свободных затухающих колебаний;
3) вынужденных колебаний.
---------------------------
Указания к заданиям № 43 – 45
Дифференциальное уравнение вынужденных гармонических колебаний пружинного маятника:
 ,
,
где δ – коэффициент затухания колебаний под действием силы сопротивления: 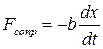 ;
;
 , где b – коэффициент сопротивления, m – масса груза;
, где b – коэффициент сопротивления, m – масса груза;
ω0 – циклическая частота свободных незатухающих колебаний пружинного маятника в отсутствии сил сопротивления и внешней вынуждающей силы;  , где k – жесткость пружины;
, где k – жесткость пружины;
F0 – амплитуда вынуждающей силы;
ω – циклическая частота вынуждающей силы.
ЗАДАНИЕ № 46
Маятник настенных механических часов представляет собой легкий стержень с грузиком. Для регулировки точности хода часов грузик можно перемещать по стержню. Как изменится период колебаний маятника, если грузик переместить с конца стержня на середину?
ВАРИАНТЫ ОТВЕТОВ:
1) увеличится в  pаз;
pаз;
2) уменьшится в  pаз;
pаз;
3) увеличится в 2 pаза;
4) уменьшится в 2 pаза;
5) увеличится в 4 pаза.
ЗАДАНИЕ № 47
На рисунке приведены 2 маятника, отличающиеся положением грузов на невесомом стержне. Укажите верные утверждения для этих маятников.

А. Момент инерции маятника I больше момента инерции маятника II.
B. Оба маятника имеют одинаковую частоту колебаний.
C. Период колебаний маятника I больше периода колебаний маятника II.
ВАРИАНТЫ ОТВЕТОВ:
1) только С;
2) А, C;
3) А, B;
4) только А;
5) только В.
---------------------------
Указания к заданиям №№ 46, 47
Момент инерции материальной точки массой m относительно оси вращения ОО’:
 , где r – расстояние от этой точки до оси вращения ОО’.
, где r – расстояние от этой точки до оси вращения ОО’.
Момент инерции системы N материальных точек относительно оси ОО’:
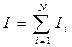 , где Ii – момент инерции i – й материальной точки относительно оси ОО’.
, где Ii – момент инерции i – й материальной точки относительно оси ОО’.
Теорема Штейнера: если момент инерции тела относительно оси ОО’, проходящей через центр масс данного тела, равен IС, то момент инерции того же тела относительно оси О1О1’, параллельной оси ОО’, равен: 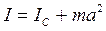 , где m – масса тела; а – расстояние между рассматриваемыми осями.
, где m – масса тела; а – расстояние между рассматриваемыми осями.
Период колебаний физического маятника:  ,
,
где I – момент инерции физического маятника относительно оси вращения,
m – масса физического маятника,
l – расстояние от центра масс физического маятника до его оси вращения.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2432; Нарушение авторских прав?; Мы поможем в написании вашей работы!