Основы теории производства

В данной лекции будет рассмотрена теория материального производства, под которым понимается процесс превращения производственных ресурсов в продукт. Теория производства изучает (прежде всего) соотношения между количеством применяемых ресурсов и объемом выпуска продукции.

Располагая факторами производства и соединяя их в различных технологиях (комбинации факторов производства), фирма выпускает готовые товары и предлагает их на рынке.

Производственная функция характеризует зависимости между количеством применяемых ресурсов, и объемом выпускаемой продукции в единицу времени и описывает множество технически эффективных способов производства. Каждый производственный процесс характеризуется определенной комбинацией ресурсов, необходимой для получения единицы продукции при данном уровне. Все факторы производства можно свести к двум - труду (L) и капиталу (K), тогда производственная функция (функция Кобба-Дугласа) примет следующий вид:

,

где А – мультипликативная форма; α и β – коэффициенты, показывающие на сколько увеличится Y при увеличении К и L на 1%.

Существует предел увеличения Y за счет увеличения затрат одного ресурса при условии, что другие ресурсы остаются неизменными.

Графически каждый способ производства может быть представлена точкой, координаты которой характеризуют необходимые для производства данного объема выпуска количества ресурсов K и L, а производственная функция – линией равного выпуска, изоквантой. Каждая изокванта представляет собой множество комбинаций производственных ресурсов и технически эффективных способов производства определенного объема продукции. Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет.

Наклон изоквант характеризует придельную норму технического замещения (MRTS – marginal rate of techniral substitution) одного ресурса другим (Q - const).

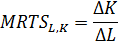
Изокванты могут иметь различную конфигурацию: линейная изокванта, изокванта характерная для случаев жесткой дополняемости ресурсов (изокванта леонтьевского типа), ломаная изокванта и гладкая изокванта.

Допустим, что фирма использует 2 ресурса и производит один продукт, такая функция является трехмерной. Для увеличения объема производства фирме следует применять капитал и труд в большем объеме, сохраняя соотношение между ними, которое задается выбранной технологией.

Отдача от масштаба – это выгодность производства в зависимости от увеличения его размеров.

Вероятно, существует объективный критерий, ставящий пределы расширения производства и задающий оптимальные размеры предприятия. Чтобы в этом разобраться, следует: ввести новые понятия, такие как общий, средний и предельный продукт; рассмотреть эту проблему с учетом фактора времени.

Убывающая отдача переменного ресурса в краткосрочном периоде. За счет чего можно увеличить объем выпуска продукции? За счет увеличения переменных ресурсов и интенсивности использования производственных мощностей.

Любой производственный процесс обладает той характерной особенностью, что если при данном количестве постоянного фактора наращивать применение переменного фактора, то производственный выпуск обязательно достигнет максимума и начнет снижаться. Указанная зависимость получила название «закона убывающей отдачи» или «убывающей предельной производительности», который говорит о том, что по мере увеличения применения переменного фактора при фиксации всех остальных всегда достигается точка, начиная с которой использование дополнительного количества переменного фактора ведет к постоянно снижающемуся приросту продукта, а затем и к его абсолютному снижению. Начиная с определенного момента последовательное присоединение дополнительной единицы переменного ресурса (например, L) к неизменному, фиксированному ресурсу (например, K) дает уменьшающийся предельный продукт в расчете на каждую последующую единицу переменного ресурса.

Снижение предельного продукта и получило название закона убывающей отдачи (закон убывающего предельного продукта, закон изменяющихся пропорций).

Отдача от масштабов производства в долгосрочном периоде. В долгосрочном периоде«фирма имеет возможность не только комбинировать факторы производства, но и изменять количество применяемых факторов, т.е. изменять масштабы производства. Оказывается, изменение факторов в одной и той же пропорции может привести к различным результатам.

Предположим, что объем применяемых ресурсов увеличивается в n раз. Как изменится объем выпускаемой продукции? Здесь возможны варианты:

1. Если выпуск увеличится тоже в n раз (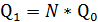), то наблюдается постоянная отдача от масштаба производства

2. Если выпуск увеличился менее, чем в n раз, то можно говорить об убывающей отдаче от роста масштаба производства.

3. Если выпуск увеличится более чем в n раз, то можно говорить о возрастающей отдаче от масштаба производства.

Лучи, проведенные из начала координат, называются линиями роста.

Используя формулу Кобба-Дугласа: экономисты пришли к выводу, что если:

1. α+β=1, то это нейтральный (или построенный) эффект от масштабов производства, означающий что увеличение от K и L в n раз приведет к увеличению объема выпуска продукции в n раз;

2. (α+β)>1, то это положительный эффект от масштабов производства, т.е. увеличение производственных ресурсов в n раз, вызовет рост объема производства в n раз;

3. (α+β)<1, то это отрицательный эффект от масштаба производства (убывающая отдача), так как увеличение ресурсов в n раз вызовет увеличение объема производства менее чем в n раз.

Дата добавления: 2014-12-16