
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Молекулярно-кинетические свойства свободнодисперсных систем
|
|
|
|
В 1827 г. Роберт Броун наблюдал под микроскопом непрерывное хаотическое движение спор папоротника. В последствии это движение получило название броуновского. Было замечено, что колебания и перемещения частиц ускорялось с уменьшением их размеров и повышением температуры (Т). В чем причина такого движения? Только в конце 19 века было высказано предположение о существовании связи между броуновским движением микрочастиц и хаотическим тепловым движением молекул среды, в которой эти частицы находились. Теоретическое обоснование эта идея получила в трудах Эйнштейна (1905 г.) и Смолуховского (1906 г.) независимо друг от друга. Правильность полученных соотношений была подтверждена эксперементально Сведбергом, Перреном, де Бройлем, Милликеном и др. Было доказано, что броуновское движение является следствием теплового движения молекул дисперсионной среды и прямым отражением законов статистики. Теория позволила экспериментально доказать реальное существование атомов и молекул, и подтвердила молекулярно-кинетическую теорию.
Рассмотрим связь между средним сдвигом частиц, участвующих в броуновском движении и коэффициентом диффузии.
Для количественного выражения броуновского движения частиц Эйнштейн и Смолуховский ввели представление о среднем сдвиге. Если фиксировать местонахождение частиц через равные промежутки времени, то наблюдается траектория движения, как показано на рисунке.
Т.к. движение происходит в трехмерном пространстве, то квадрат среднего расстояния, проходимого за любой промежуток времени 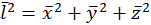 , под микроскопом на плоскости
, под микроскопом на плоскости 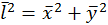 .
.
При равновероятных отклонениях напрвление движения находится между x и y под углом в 45°, тогда 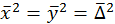 или
или 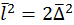 ,
, 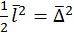 , где
, где  – среднее значение сдвига (смещения) за время τ по выбранному направлению x или y.
– среднее значение сдвига (смещения) за время τ по выбранному направлению x или y.
Если броуновское движение является следствием теплового движения молекул среды, то можно говорить о тепловом движении частиц дисперсной фазы. Следовательно, дисперсная система должна подчиняться законам молекулярно-кинетической теории, приложенным к газам или растворам. Для доказательства этой гипотезы был выбран один из законов молекулярно-кинетической теории – закон диффузии, согласно которому хаотичность броуновского движения должна приводить к выравниванию концентрации дисперсной фазы по всему объему среды.
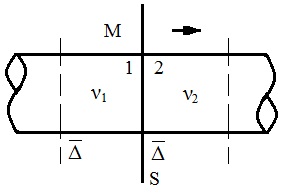
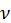 – частичная концентрация,
– частичная концентрация, 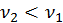
 – смещение за время τ
– смещение за время τ
Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от MN. Q1 – количество дисперсной фазы, которое перемещается за время τ из 1 отсека вправо:
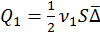 ,
,
т.е. половина того, что было в первом отсеке. За это время в обратном направлении из 2 отсека переместится:
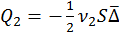 .
.
Суммарное количество дисперсной фазы, перемещенное вправо через поперечное сечение MN:
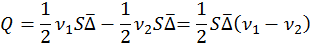
Градиент концентрации
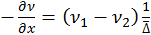 или
или 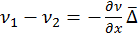 , тогда
, тогда 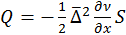 .
.
Сравним полученное выражение с известным законом Фика для диффузии:
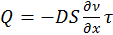 , тогда
, тогда 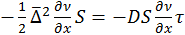 ,
, 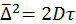 – уравнение Эйнштейна-Смолуховского, где D – коэффициент диффузии, [м2/с].
– уравнение Эйнштейна-Смолуховского, где D – коэффициент диффузии, [м2/с].
Согласно уравнению Эйнштейна: 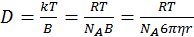 .
.
Для сферических частиц 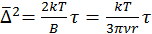 .
.
С помощью уравнения Эйнштейна-Смолуховского было вычислено значение числа Авогадро NA = (5-7)·1023 молек/моль.
Известно что хаотическое тепловое движение молекул измеряется в еденицах kT, в таких же единицах измеряется и броуновское движение частиц, состоящих из большого числа молекул: 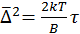 , что и предполагалось доказать, т.е. природа броуновского явления была объяснена.
, что и предполагалось доказать, т.е. природа броуновского явления была объяснена.
Диффузия присуща как микро-, так и макросистемам и отличается лишь скоростью процесса. Перрен вывел зависимость между D и молекулярной массой ВМС.
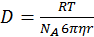 ;
; 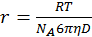 ;
; 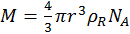 ;
; 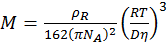 .
.
Т.о., используя уравнение Эйнштейна, можно определить размер частиц золей и молекулярную массу полимеров.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 608; Нарушение авторских прав?; Мы поможем в написании вашей работы!