Основные сведения. Пакет анализа - это надстройка, предназначенная для статистического анализа данных

Пакет анализа - это надстройка, предназначенная для статистического анализа данных. В пакет анализа входят следующие программы:

· Однофакторный дисперсионный анализ.

· Двухфакторный дисперсионный анализ с повторением.

· Двухфакторный дисперсионный анализ без повторений.

· Корреляция.

· Ковариация.

· Описательная статистика.

· Экспоненциальное сглаживание.

· Двухвыборочный F- тест для дисперсии.

· Анализ Фурье.

· Гистограмма.

· Скользящее среднее.

· Генерация случайных чисел.

· Ранг и персентиль.

· Регрессия.

· Выборка.

· Парный двухвыборочный t-тест для средних.

· Двухвыборочный t-тест с одинаковыми дисперсиями.

· Двухвыборочный t-тест с разными дисперсиями.

· Двухвыборочный z-тест для средних.

Установка пакета анализа необходимо выполнить команду Сервис\Надстройки. Если пакет анализа установлен, в меню Сервис появляется команда Анализ данных. Для загрузки необходимой для расчета программы следует выполнить команду Сервис/Анализ данных и далее выбрать программу из списка.

Описательная статистика.

Рассмотрим пример применения пакета анализа для сравнения двух групп - экспериментальной и контрольной. Из числа членов генеральной совокупности в случайном порядке сформированы две группы учащихся. В ходе эксперимента получены следующие баллы по учебному предмету:

Результаты эксперимента

(введены в электронную таблицу )

	А	В
	эксперименталь-ная группа	контрольная группа

Рисунок 8

Для получения статистических характеристик экспериментальной и контрольной групп можно использовать статистические функции, входящие в список функций Excel, или программу Описательная статистика, включенную в Пакет анализа.

На рисунке 9 приведено диалоговое окно программы Описательная статистика, в которое введены параметры для рассматриваемого примера.

Входной и выходной интервалы можно указать с помощью мыши.

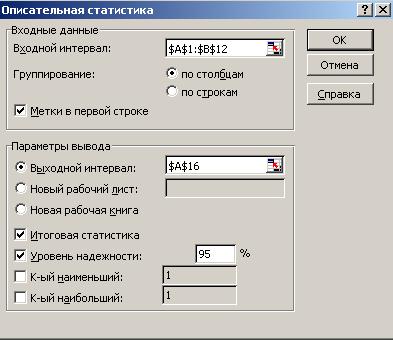
Рисунок 9

Результаты работы программы после обработки данных программой Описательная статистика приведены на рисунке 10.

экспериментальная группа	контрольная группа
Среднее	13,63	Среднее	9,44
Стандартная ошибка	0,742	Стандартная ошибка	0,689
Медиана		Медиана
Мода		Мода
Стандартное отклонение	2,460	Стандартное отклонение	2,068
Дисперсия выборки	6,054	Дисперсия выборки	4,278
Эксцесс	0,427	Эксцесс	0,129
Асимметричность	-0,1757	Асимметричность	-0,1013
Интервал		Интервал
Минимум		Минимум
Максимум		Максимум
Сумма		Сумма
Счет		Счет
Уровень надежности(95,0%)	1,653	Уровень надежности(95,0%)	1,589

Рисунок 10

Проверка статистических гипотез.

Метод статистических гипотез широко применяется в научной деятельности для оценки результатов эксперимента. Как правило, при проведении научного исследования приходится выполнять сравнительные оценки генеральных параметров по различиям, наблюдаемым между выборками. О преимуществе той или иной из сравниваемых групп обычно судят по разности между средними долями и другими выборочными показателями.

При проведении статистической обработки результатов эксперимента выдвигается нулевая гипотеза (Н₀), которая сводится к тому, что разница между генеральными параметрами сравниваемых групп равна нулю и что различия, наблюдаемые между выборочными характеристиками, носят случайный характер. В другой, альтернативной гипотезе делается предположение о преимуществе нового метода.

Альтернативные гипотезы принимаются только тогда, когда опровергается нулевая гипотеза. Это возможно в тех случаях, когда различия в средних выборочных настолько значимы (статистически достоверны), что риск ошибки отвергнуть нулевую гипотезу и принять альтернативную не превышает одного из трех принятых уровней значимости статистического вывода:

· первый уровень - 5% (допускается риск ошибки вывода в пяти случаях их ста таких же экспериментов при строго случайном отборе в выборочную совокупность);

· второй уровень 1% (допускается риск ошибиться только в одном случае из ста;

· третий уровень 0,1% (допускается риск ошибиться только в одном случае из тысячи).

Существует два вида статистических критериев - параметрические и непараметрические. Параметрические критерии служат для проверки гипотез о параметрах совокупностей, распределяемых по нормальному закону. Рассмотрим пример применения одного из параметрических критериев - t-критерия Стьюдента для сравнительной оценки средних величин, рассчитанных для контрольной и экспериментальной групп в рассматриваемом примере. Для выполнения расчета вызовем программ у Двухвыборочн ый t-тест с разными дисперсиями, входящую в Пакет анализа и введем данные в диалоговое окно. Для ввода исходного диапазона блок данных можно выделить непосредственно в таблице. Уровень значимости задается в поле Альфа вводом значения с клавиатуры, в поле Выходной интервал указывается адрес верхней левой ячейки области размещения выходных таблиц. Выходные таблицы могут быть размещены на том же рабочем листе, на другом листе или в другом файле.

Результаты обработки данных приведены на рисунке 12.

Двухвыборочный t-тест с различными дисперсиями
	экспериментальная группа	контрольная группа
Среднее	13,63	9,44
Дисперсия	6,054	4,278
Наблюдения
Гипотетическая разность средних
df
t-статистика	4,029
t критическое двухстороннее	2,101

Рисунок 11

Сравнение полученной t-статистики (4,029) с t табличным (2,100) свидетельствует о том, что есть основание принять альтернативную гипотезу о том, что учащиеся экспериментальной группы показывают более высокий уровень знаний.

В случаях, когда необходимо оценить эффективность проведенной экспериментальной работы в одной группе, используется парный двухвыборочный t-тест для средних.

Однофакторный дисперсионный анализ.

Однофакторный дисперсионный анализ применяют в тех случаях, когда может быть указан один фактор, влияющий на конечный результат, и этот фактор может принимать конечное число значений (уровней). Типичный пример задачи однофакторного анализа - сравнение по достигаемым результатам нескольких различных способов действия, направленных на достижение одной цели, например, нескольких школьных учебников, различных доз удобрений, нескольких лекарств.

Рассмотрим применение метода на следующем примере:

Для выяснения влияния денежного стимулирования на производительность труда шести однородным группам из 5 человек были предложены задачи одинаковой трудности. Задачи предлагались испытуемому независимо от всех остальных. Группы различаются между собой величиной денежного вознаграждения за решаемую задачу. Группы упорядочены по возрастанию влияния фактора.

Исходные данные группируются в виде таблицы, в которой градации регулируемого фактора располагаются по горизонтали в верхней части таблицы, а числовые значения признака размещаются по градациям фактора.

A B C D E

	Влияние величины вознаграждения на производительность труда
	гр.1	гр.2	гр.3	гр.4	гр.5

Рисунок 12

Если регулируемый фактор (размер вознаграждения) оказывает существенное влияние на результативный признак (количество решенных задач), то это скажется на величине групповых средних, которые будут заметно отличаться друг от друга.

Нулевая гипотеза сводится к предположению, что генеральные межгрупповые средние и дисперсии равны между собой, а различия, наблюдаемые между выборочными показателями, вызваны случайными причинами, а не влиянием на признак регулируемого фактора. Нулевую гипотезу отвергают, если дисперсионное отношение F_ф 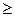F_ст (критерий Фишера) для принятого уровня значимости - a.

Для проведения однофакторного анализа введем исходные данные в таблицу в форме представленной на рисунке 13.

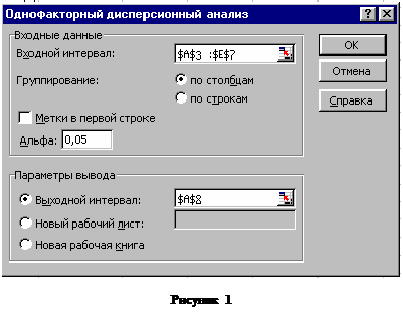Выполним команду Сервис/Анализ данных, в открывшемся списке выберем Однофакторный дисперсионный анализ и зададим параметры в диалоговом окне. Для ввода исходного диапазона блок данных можно выделить непосредственно в таблице. Уровень значимости задается в поле Альфа вводом значения с клавиатуры, в поле Выходной интервал указывается адрес верхней левой ячейки области размещения выходных таблиц. Выходные таблицы могут быть размещены на том же рабочем листе, на другом листе или в другом файле.

ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Столбец 1
Столбец 2			11,8	9,2
Столбец 3			13,6	10,3
Столбец 4			15,6	6,3
Столбец 5			22,6	15,3
ANOVA
Источник вариации	SS	df	MS	F	P-Значение	F критическое
Между группами	474,64		118,66	12,86985	2,41219E-05	2,866080706
Внутри групп	184,4		9,22
Итого	659,04

Рисунок 14

На рисунке 14 показан результат работы программы. В таблице ANOVA

SS -сумма квадратов,

df -число степеней свободы,

MS - средние квадраты,

F - дисперсионное отношение (отношение MS между группами к MS внутри групп). Значение F используется для проверки нулевой гипотезы.

F критическое - табличная величина, критические значения F определены для нескольких уровней значимости (0,1; 0,05; 0,01).

Из таблицы видно, что фактическое значение F, больше критического значения, поэтому гипотеза об отсутствии влияния фактора на исследуемый признак (нулевая гипотеза) должна быть отвергнута. Этот результат позволяет сделать заключение о том, что варьирование признака по группам достаточно велико, чтобы быть предметом статистического анализа.

Регрессионный анализ

Регрессионный анализ позволяет найти уравнение, которое наилучшим образом описывает множество данных или позволяет выяснить, что подходящего уравнения нет. По экспериментальным измерениям влияния одной величины на другую с помощью регрессионного анализа можно установить аналитический закон связи между этими величинами. В экономике регрессионный анализ позволяет спрогнозировать динамику продаж в зависимости от уровня цен на товары по предыстории влияния цен на оборот.

Линейный регрессионный анализ заключается в подборе линейной функции, описывающей входные данные, с помощью метода наименьших квадратов. То есть необходимо найти уравнение вида

Y=kx+b,

Где y – функция, описывающая входные данные и зависящая от переменной х,

k и b – параметры уравнения, которые нужно определить.

Исходные данные для регрессионного анализа находятся в таблице.

Таблица отображает экспериментальные измерения температуры и давления. Необходимо определить, насколько влияет температура на давление, и построить уравнение для этих двух величин.

Для этого необходимо:

· выбрать в меню команду Сервис/Анализ данных;

· Щелкнуть по строке Регрессия.

В диалоговом окне Регрессия

· щелкнуть мышью в поле ввода Входной интервала Y в группе элементов управления Входные данные и выделить диапазон ячеек С1:С6;

· Щелкнуть мышью на поле ввода Входной интервал Х и выделить диапазон ячеек В1:В6;

· Установить флажок Метки в группе элементов Входные данные, так как указанные диапазоны содержат названия.

· Установить параметр Новый рабочий лист и нажать ОК.

Дата добавления: 2014-11-28