Побудова аксонометрії поверхонь обертання

Методичні вказівки до розв’язання задачі 7 листа 6

Сферу утворює коло, яке обертається навколо кола. Таким чином, будь-яка точка F є тією, що належить до одного з кіл сфери. Щоб визначити розмір діаметру цього кола можна використати допоміжну січну площину (горизонтальну, фронтальну, профільну), яка на відповідній площині проекції дасть змогу побудувати це коло і точку F на ньому.

Комплексне креслення сфери: всі проекції – коло з діаметром D, кожне з яких є контурною твірною (екватор, фронтальний меридіан, профільний меридіан).

Натуральною величиною перерізу сфери січною площиною завжди буде коло. Розмір діаметру цього кола дорівнює розміру відрізка вздовж по січній площині від однією точки зустрічі з контурною твірною сфери до другої, через які проходить січна. Перпендикулярна лінія з центра сфери до сліду січної площини поділить її навпіл, що дасть змогу заміряти радіус цього кола (перерізу).

Зразок оформлення задачі 7 на рисунку 16.

На вільному місті формату побудувати прямокутну ізометрію циліндру, конусу та сфери. Аксонометричні осі x', y' та z' розташовані під кутом 120º. Коло в аксонометрії еліпс. Мала вісь еліпсу – відсутня вісь площини проекцій, на якій накреслено коло. Велика вісь перпендикулярна до малої. Велика вісь дорівнює 1,22D, а мала вісь – 0,71D. Додаткові точки еліпсу, точки по колу на відповідних координатних осях, тобто від центру на відстані, що дорівнює радіусу кола.

Аксонометрія циліндру – дві основи (еліпси) та дві дотичні твірні до них. Аксонометрія конусу – основа (еліпс) та дві дотичні твірні до нього. Аксонометрія сфери – три контурні твірні (еліпси) та дотичне коло до них.

Видимість геометричної поверхні визначає позитивний напрямок осей, на яких розташована поверхня.

Рисунок 16 – Зразок оформлення задачі 7 листа 6

Лист 7. Задача 8. Формат А3, масштаб 1:1.

Задача 8. Побудувати три проекції геометричної поверхні з отвором та натуральну величину перерізу площиною ∑.

Дано: дві проекції геометричної поверхні з отвором (рисунок 17),

D_к=70+Nвар+Nгр, D₀=55+Nвар+Nгр, Х₀=100-2Nвар+Nгр,

α=(25+Nвар+Nгр)º,

де Nвар – номер варіанту; Nгр – остання цифра у номері групи.

Рисунок 17 – Завдання до задачі 8 листа 7

Лист 8. Задача 9. Формат А3, масштаб 1:1.

Задача 9. Побудувати три проекції геометричної поверхні з отвором та натуральну величину перерізу площиною ∑.

Дано: дві проекції геометричної поверхні з отвором (рисунок 18),

а=30+Nвар+Nгр, Z_k=40+Nвар+Nгр, α=(10+Nвар+Nгр)º,

де Nвар – номер варіанту; Nгр – остання цифра у номері групи.

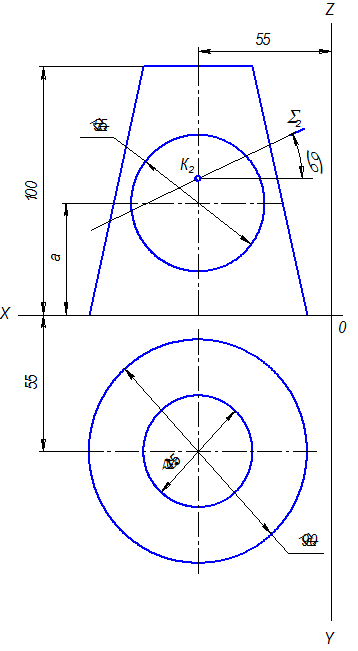
Рисунок 18 – Завдання до задачі 9 листа 8

Лист 9. Задача 10. Формат А3, масштаб 1:1.

Задача 10. Побудувати три проекції геометричної поверхні з отвором та натуральну величину перерізу площиною ∑.

Дано: дві проекції геометричної поверхні з отвором (рисунок 19),

D=80+Nвар+Nгр, а=12+0,5Nвар+Nгр, α=(30+Nвар+Nгр)º,

де Nвар – номер варіанту, Nгр – остання цифра у номері групи.

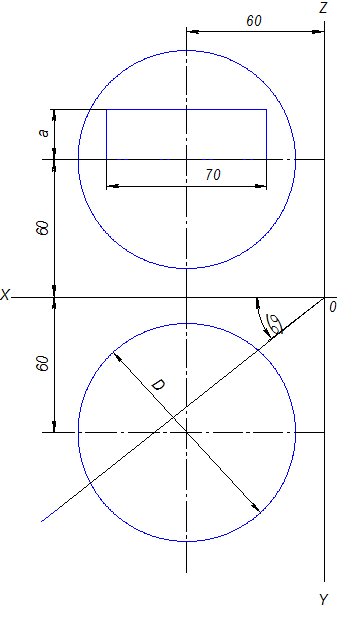
Рисунок 19 – Завдання до задачі 10 листа 9

Дата добавления: 2014-12-16