Краткая теория. Цель работы: проверить выполнение соотношения неопределенностей для фотонов

ПРОВЕРКА СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ ДЛЯ ФОТОНОВ

ЛАБОРАТОРНАЯ РАБОТА 14

Цель работы: проверить выполнение соотношения неопределенностей для фотонов.

Приборы и принадлежности: гелий-неоновый лазер непрерывного действия, дифракционная щель, экран, оптическая скамья с рейтерами, миллиметровая шкала.

Результаты изучения таких физических явлений, как излучение абсолютно черного тела, фотоэффект, эффект Комптона служат доказательством квантовых (корпускулярных) представлений о свете, как о потоке фотонов. С другой стороны, явления интерференции, дифракции и поляризации света убедительно подтверждают волновую (электромагнитную) природу света. Наконец, давление и преломление света объясняется как волновой, так и квантовой теориями. Таким образом, электромагнитное излучение обнаруживает удивительное единство, казалось бы, взаимоисключающих свойств - непрерывных (волны) и дискретных (фотоны), которые дополняют друг друга.

Уравнения

ε_ф = h ν; р _ф = h / λ = h ν/ с (14.1)

связывают корпускулярные свойства света (энергия ε_ф и импульс р _ф фотона) с волновыми (частота ν и длина волны λ). Здесь h - постоянная Планка, равная 6,625∙10 ^{- 34} Дж∙с.

Более детальное рассмотрение оптических явлений приводит к выводу, что свойствам непрерывности, характерным для электромагнитного поля световой волны, не следует противопоставлять свойства дискретности, характерные для фотонов. Свет, обладая одновременно корпускулярными и волновыми свойствами, обнаруживает определенные закономерности их проявления. Чем больше длина волны, тем меньше энергия и импульс фотона, и тем труднее обнаруживаются квантовые свойства света. С этим связано, например, существование красной границы фотоэффекта. Наоборот, чем меньше длина волны излучения, тем больше энергия и импульс фотона, и тем труднее обнаружить волновые свойства света. Например, волновые свойства рентгеновского излучения обнаружены лишь после применения кристаллов в качестве дифракционной решетки. Подробнее рассмотрим взаимосвязь между волновыми и корпускулярными свойствами света на примере дифракции лазерного излучения на прямоугольной щели.

Дифракция света – явление огибания световой волной препятствий в виде непрозрачных и прозрачных тел, узких отверстий, резких неоднородностей среды, в результате чего свет проникает в область геометрической тени и происходит интерференционное перераспределение света в пространстве.

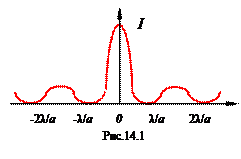
Дифракция характерна для волн любой природы. Для световых волн дифракция отчетливо наблюдается, если размер преграды r соизмерим с длиной волны λ (r ~ λ). Известно, что при дифракции на преграде в виде прямоугольной щели с шириной а дифракционная картина на экране наблюдения будет иметь следующий вид (рис14.1): в центре экрана - главный максимум, образованный неотклоненными (недифрагированными) лучами, по обе стороны от главного максимума - чередующиеся минимумы и максимумы убывающей интенсивности). Условие дифракционных максимумов при дифракции на щели имеет вид

a ·sinφ = (2 m +1) ·λ/2. (14.2)

Дифракционные минимумы соответствуют условию

a sinφ = 2 m λ/2 = m λ. (14.3)

Здесь φ - угол дифракции; m - порядок дифракционного максимума или минимума. Для центрального максимума угол дифракции φ = 0. В этом направлении свет имеет наибольшую интенсивность и образует максимум нулевого порядка. В направлении угла φ, арксинус которого равен λ/ a, интенсивность равна нулю (первый дифракционный минимум, m = 1). Его интенсивность значительно меньше максимума при φ = 0. Второму минимуму соответствует угол φ = arc sin2λ / а и т.д.

Если рассматривать излучение как поток фотонов, дифракция света на щели состоит в том, что при прохождении фотонов через щель происходит их перераспределение в пространстве. Так как вероятность попадания фотонов в различные точки экрана неодинакова, то и возникает дифракционная картина. Освещенность экрана пропорциональна вероятности попадания фотонов на единицу площади экрана. С другой стороны, по волновой теории освещенность пропорциональна квадрату амплитуды световой волны в той же точке экрана. Следовательно, квадрат амплитуды световой волны в данной точке пространства является мерой вероятности попадания фотонов в данную точку. Как и для любых частиц, для фотонов справедливо соотношение неопределенностей Гейзенберга

Δ х ·Δ р_х ≥ h, (14.4)

где Δ х - область локализации частицы (неопределенность координаты), Δ р_х - область значений компоненты импульса (неопределенность импульса). Выражения аналогичные (14.4) можно записать для осей у и z.

Соотношение (14.4) обозначает, что любой объект микромира (микрочастицу, в данном случае фотон) невозможно одновременно характеризовать точно значением координаты х и импульса р_х, как это можно сделать для объектов макромира, описываемого классической механикой.

Если частица находится в состоянии с точным значением координаты х (неопределенность Δ х = 0), то соответствующая проекция импульса Δ р_х оказывается совершенно неопределенной, т.е. Δ р_х → ∞, и наоборот, при Δ р_х = 0 Δ х → ∞.

Отсюда вытекает фактическая невозможность одновременного определения точного значения координаты и импульса частицы. Соотношение неопределенностей (14.4) можно записать и для других физических величин:

координаты и скорости: Δ х ·Δv _х ≥ h / m, (14.5)

энергии и времени: Δ Е ·Δ t ≥ h. (14.6)

Из связи энергии с частотой Е = h ν и соотношения (14.6) видно, что частота излучаемого фотона также должна иметь неопределенность

Δν ≥ ΔЕ/ h, (14.7)

т.е. линии спектра, возникающие в результате излучения волны возбужденным атомом, должны характеризоваться некоторым разбросом частот Δν. Действительно, опыт показывает, что спектральные линии всегда размыты. И даже в случае излучения лазера, обладающего высокой степенью монохроматичности, нельзя говорить об абсолютно точном значении частоты или длины волны. Измеряя ширину спектральной линии, можно оценить порядок времени жизни атома в возбужденном состоянии.

Неопределенности координат, импульса и других физических характеристик макрообъектов из-за малого значения постоянной Планка h малы настолько, что ими можно пренебречь и говорить о точных значениях этих величин, определяемых в рамках классической физики.

Учитывая соотношение неопределенностей в виде (14.4) и сосредоточенность энергии волны в области нулевого максимума, ограниченного по обе стороны минимумами первого порядка, можно картину дифракции интерпретировать как проявление соотношения неопределенностей для фотонов.

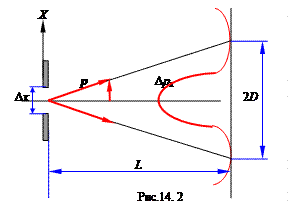
Ширину щели a представим как неопределенность координаты (рис.14.2), тогда ширина нулевого максимума пропорциональна неопределенности импульса фотона Δ р_х. Действительно, в области угла φ мы не можем точно указать импульс р_х = m _· v _х, т.е. строгое направление скорости движения фотона, но можем с достоверностью утверждать, что разброс различных направлений импульсов лежит а пределах угла φ.

Из рис. 14.2 видно, что

Δ р _х = р sinφ, (14.8)

где р - импульс в направлении φ; φ- угол, соответствующий первому минимуму.

Синус угла φ можно определить экспериментально из соотношения

sinφ₁ ≈ tgφ₁ = D / L. (14. 9)

Импульс частицы можно связать с присущей ей длиной волны по формуле де Бройля

λ = h / р = h / m v, (14.10)

где v - скорость движения частицы; m - ее масса.

Соотношение де Бройля справедливо не только для фотонов, но и для любых микрочастиц, электронов, нейтронов, протонов и т.д. Суть идеи де Бройля в том, что волновые свойства присущи не только частицам света, но и всем другим частицам. С учетом того, что Δ х = а,и формул (14.8) - (14.10) соотношение (14.5) перепишется в виде, удобном для экспериментальной проверки:

а D

--------- ≥ 1. (14.11)

λ L

Обозначим левую часть неравенства буквой F, тогда для максимума нулевого порядка параметр F = 1 и не должен зависеть от ширины щели.

Дата добавления: 2014-12-16