Пример выполнения лабораторной работы (Ч. 2)

Задача 2.1. Путем опроса получены следующие данные (n =80):

2 4 2 4 1 1 1 2 0 6	1 2 1 2 2 4 1 1 5 1	0 2 4 1 2 2 1 1 1 1
1 1 1 1 2 1 1 4 1 1	7 4 1 4 2 1 2 1 1 1	4 1 1 4 5 1 4 2 4 5
1 6 4 1 1 2 4 1 1 1	0 0 4 6 4 7 4 1 1 5

Выполнить задания:

а) получить дискретный вариационный ряд и статистическое распределение выборки;

б) построить полигон частот;

в) составить ряд распределения относительных частот;

г) составить эмпирическую функцию распределения;

д) построить график эмпирической функции распределения;

е) найти основные числовые характеристики вариационного ряда (по возможности использовать упрощающие формулы для их нахождения):

1) выборочное среднее ;

2) выборочную дисперсию D (X);

1) выборочное среднее квадратическое отклонение ;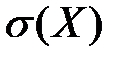

4) коэффициент вариации V;

5) интерпретировать полученные результаты.

Решение.

а) Для составления дискретного вариационного ряда отсортируем данные опроса по величине и расположим их в порядке возрастания:

0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 6 6 6 7 7.

Статистическое распределение выборки представлено в таблице 6.1, в которой первая строка – варианты (наблюдаемые значение), вторая строка – частоты появления этих вариант).

Таблица 6.1. Варианты и их частоты

xi
ni

б) Для построения полигона частот найдем относительные частоты (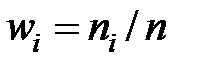, где 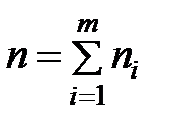, где m – число различных значений признака X () и в данном примере m= 8), которые будем вычислять с одинаковой точностью. Полигон частот – ломаная линия, соединяющая точки с координатами 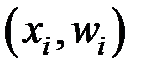(Рис. 6.1). Расчеты запишем в табл. 6.2.

Таблица 6.2. Относительные частоты и накопленные частоты

xi	ni	Относительные частоты	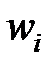Накопленные частоты
		0.050	0.050
		0.161	0.211
		0.175	0.188
		0.100	0.688
		0.200	0.888
		0.050	0.918
		0.018	0.975
		0.025	1.000
Сумма

Рис. 6.1. Полигон частот вариационного ряда

в) Запишем ряд распределения (табл. 6.1) относительных частот в виде таблицы 1, в которой первая строка – варианты (изучаемый признак), вторая строка – относительные частоты (частости).

Таблица 6.1. Распределение относительных частот появления признака

xi
ni	0.05	0.161	0.175	0.1	0.2	0.05	0.018	0.025

г) Эмпирическую функцию распределения найдем, используя накопленные частоты (табл. 6.1, столбик 4) и формулу (4.1):

д) Построим график эмпирической функции распределения (рис. 6.2), используя значения, полученные в пункте г).

Рис. 6.2. График эмпирической функции распределения

е) Для вычисления выборочного среднего и выборочной дисперсии с использованием приведенных выше формул, удобно составлять расчетную таблицу 6.2:

Таблица 6.2. Расчетная таблица для вычисления выборочных величин

xi	ni	xi 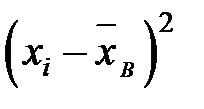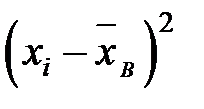× ni		× ni
			8.1796	12.7184
			1.4596	44.9748
			0.7196	10.1544
			0.0196	0.4704
			1.2996	20.7916
			4.5796	18.1184
			9.8596	29.5788
			17.1196	14.2792
Сумма				191.488

Используя суммы, полученные в табл. 6.2, определим искомые величины.

1) Выборочную среднюю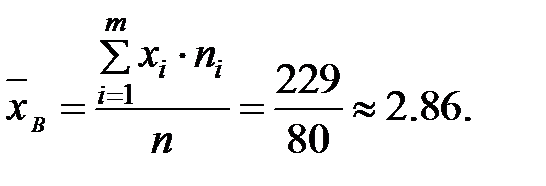

2) Выборочную дисперсию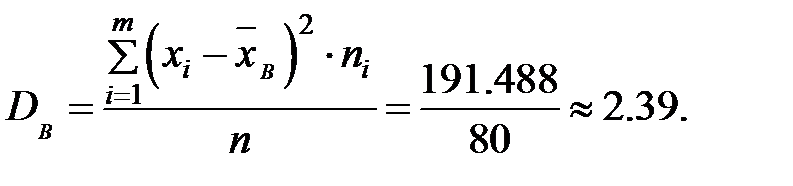

1) Выборочное среднее квадратическое отклонение

4) Коэффициент вариации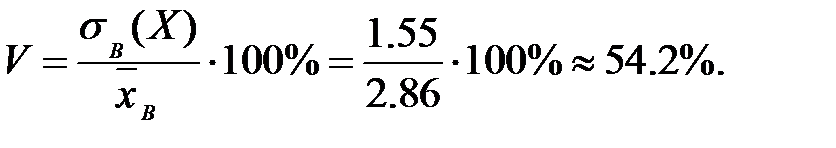

5) Интерпретация полученных результатов:

- величина характеризует среднее значение признака X;

- среднее квадратическое отклонение 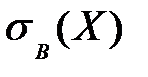описывает абсолютный разброс значений показателя X относительно среднего значения и в данном случае составляет ;

- коэффициент вариации V характеризует относительную изменчивость показателя X, то есть относительный разброс вокруг его среднего значения 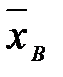, и в данном случае составляет .

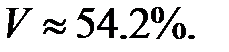Ответ: ; ; ;

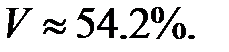
Задача 2. См. задание 2 в КР 3 (часть 2)

Алгоритм выполнения задания по проверке статистической гипотезы о виде распределения [1]

1. Определить размах выборки: R= X_Max - X_Min.

2. Назначить число карманов, m =8 (любое число от 7 до 25).

3. Найти среднее значение (М) и стандартное отклонение (s).

4. Найти левые и правые границы для карманов, пронумерованных от 0 до m. При этом для кармана № 0 правая граница равна минимуму, для кармана № 1 правая граница равна минимальному значению плюс длина кармана, и т.д.

5. Построить гистограмму и выдвинуть гипотезу о виде распределения.

6. Найти значения предполагаемой ФР на границах карманов:

Так, для нормального распределения существует встроенная функция НОРМРАСПР(), где в качестве последнего аргумента печатаем ИСТИНА.

7. Найти теоретические вероятности попадания в карман (разность ФР по границам карманов).

8. Найти теоретические частоты (произведение теоретических вероятностей попадания в карман на объем выборки).

9. Вычислить столбец величин:

(выборочная частота-теоретическая частота)^2 / теоретическая частота.

Сумма этих величин является значением выборочного c²_выб критерия.

10. Найти значение теоретического критерия согласия c²_теор при заданном уровне значимости (у нас 0.05) можно по формуле ХИ2ОБР (вероятность; число степеней свободы), где число степеней свободы k = m -1- r, например, r =2 для нормального распределения.

11. Сравниваем c²_выб с c²_теор, делаем вывод: если c²_выб < c²_теор, то нет оснований отвергать основную гипотезу, в противном случае основная гипотеза не принимается.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература

1. Попов А. М. Сотников В.Н. Высшая математика для экономистов: учебник для бакалавров / А. М. Попов, В. Н. Сотников; под ред. проф.А. М. Попова. — М.: Издательство Юрайт, 2012. — 564 с.

2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для бакалавров /В. Е. Гмурман. — 11-е изд., перераб. и доп. — М.: Издательство Юрайт, 2013. — 404 с.

3. Шапкин А.С. Задачи по высшей матем., теории вероятностей, математической статистике, математическое программирование с решениями. М.: Изд-торг корп Дашков и Ко; 2011г.

4. Дополнительная литература

5. Геворкян П.С. Теория вероятностей и математическая статистика: Курс лекций/ П.С. Геворкян, А.В. Потемкин, И.М. Эйсымонт.— М.: Экономика, 2013

6. Кремер Н. Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Математика для экономистов: от Арифметики до Эконометрики: учеб. справ. пособие для бакалавров / под ред.Н. Ш. Кремера. — 3-е изд., перераб. и доп. — М.: Издательство Юрайт; ИД Юрайт, 2012. — 685 с.

7. Кремер Н.Ш. Теория вероятностей и математическая статистика. —М.: ЮНИТИ, 2003, 2004, 2007.

8. Браилов А.В., Солодовников А.С. Сборник задач по курсу «Математика в экономике». Часть 3. Теория вероятностей. — М.: Финансы и статистика, 2010.

9. Денежкина И.Е., Орлова М.Г., Швецов Ю.Н. Основы математической статистики. Учебно-методическое пособие для самостоятельной работы бакалавров. — М.: Финансовая академия при правительстве РФ, 2010.

10. Потемкин А.В., Фридман М.Н., Эйсымонт И.М. Теория вероятностей и математическая статистика. Учебно-методическое пособие для студентов заочной формы обучения. Для бакалавров направления 080100.62 «Экономика». — М.: Финуниверситет, 2013.

11. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. Учебник в 3 ч. Ч.3. Теория вероятностей и математическая статистика. — М.: Финансы и статистика, 2008.

12. Теория вероятностей и математическая статистика. Компьютерная обучающая программа. Под общей редакцией Кремера Н.Ш. — М.: Финуниверситет, 2012.

Дата добавления: 2014-12-16