
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Краткие сведения из теории. Преобразование на кусочно-параболическом участке ВАХ
|
|
|
|
Преобразование на кусочно-параболическом участке ВАХ
3.14 Установить ЕСМ=ЕСМ2=u0
3.15 Установить амплитуды сигналов U1m=U2m=½ u0/2½
3.16 Повторить п. 3.5 для новых параметров сигналов.
Содержание отчета
1. Принципиальная схема исследования.
2. Сток-затворная характеристика исследованной нелинейной цепи.
3. Аппроксимация ВАХ для работы на квадратичном (параболическом), кусочно-линейном и кусочно-параболическом участках.
4. Теоретический расчет спектра для данных, использованных в эксперименте (по указанию преподавателя).
5. Осциллограммы и спектры исследованных процессов.
Контрольные вопросы:
1. Каковы характерные особенности спектров тока, протекающего через нелинейный безинерционный элемент, при моно- и бигармоническом воздействиях?
2. Что называется порядком комбинационного колебания? Поясните примером.
3. Какова связь между наивысшим порядком комбинационного колебания и степенью полинома, аппроксимирующего характеристику нелинейного элемента?
4. Перечислите наиболее часто применяемые методы спектрального анализа колебаний на выходе без инерционных нелинейных преобразователей. Укажите, при каких видах аппроксимации целесообразно применять каждый из них.
5. Что называется углом отсечки, как определить его по осциллограмме сигнала и как выразить аналитически?
6. Характеристика нелинейного элемента аппроксимирована ломаной линией. Входное воздействие представляет собой сигнал вида u=ЕСМ+Umcos2wt. Пользуясь системой трех координатных плоскостей, покажите, как следует выбрать ЕСМ и Um, чтобы:
а) ток по форме повторял форму входного сигнала;
б) ток принял форму косинусоидальных импульсов с углом отсечки 900.
7. Поясните, как работает преобразователь, принципиальная схема которого приведена на рисунке 3.4.
8. Как практически изменить положение рабочей точки на сток-затворной характеристике полевого транзистора?
9. Перечислите все составляющие спектра тока, если на вход нелинейного элемента с параболической (квадратичной) ВАХ подать гармонические сигналы с частотами 5 и 6 КГц.
10. То же для случая аппроксимации ВАХ степенным полиномом третьей степени.
11. Как изменится спектральный состав тока, если амплитуду входного напряжения уменьшить в 10 раз?
ЛАБОРАТОРНАЯ РАБОТА №4
"ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ ВО ВРЕМЕНИ
(ТЕОРЕМА КОТЕЛЬНИКОВА)"
Цель работы: исследование процессов дискретизации и восстановления непрерывных сигналов.
Некоторые из непрерывных сигналов имеют ограниченный спектр. Для таких сигналов справедлива теорема Котельникова: непрерывный сигнал с ограниченным спектром полностью определяется своими значениями в дискретные моменты времени, отстоящими друг от друга на время  , где Fв – верхняя граничная частота спектра этого сигнала,
, где Fв – верхняя граничная частота спектра этого сигнала,  t – называется интервалом дискретизации по времени.
t – называется интервалом дискретизации по времени.
| U(t) |
| E(t) |
| Z(t) |
| U(t) |
| 0,1 0,5 0,3 0,3 0,2 0,4 |
| -0,4 -0,1 0,4 |
| 6,0 5,0 5,0 4,0 3,0 3,0 3,0 3,0 3,0 2,0 2,0 2,0 2,0 2,0 2,0 |
| 5,6 4,8 3,1 2,9 2,5 2,3 3,0 2,0 2,3 2,4 2,0 2,0 2,0 1,9 |
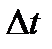 2 2  3 3  4 4  5 5  6 6  7 7  8 8  9 9  10 10 
|
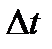 2 2  3 3  4 4  5 5  6 6  7 7  8 8  9 9  10 10 
|
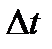 2 2  3 3  4 4  5 5  6 6  7 7  8 8  9 9  10 10 
|
| t |
| t |
| t |
| t |
| непрерывный сигнал |
| импульсный сигнал |
| дискретный сигнал |
| ошибка квантования |
Рисунок 4.1 Дискретизация сигнала
На основе теоремы Котельникова непрерывный сигнал с ограниченным спектром может быть передан путем передачи его мгновенных значений, отсчитываемых в дискретные моменты времени – дискретных отсчетов, т. е. фактически задача сводится к передаче последовательности чисел.
Эта теорема указывает следующие условия:
а) спектр передаваемого сигнала должен быть ограничен верхней граничной частотой Fв;
б) частота следствия импульсов – отсчетов или частота дискретизации Fg.
Fg  (4.1)
(4.1)
Если истинное мгновенное значение сигнала U(t), подлежащее передаче попадает между разрешенными значениями, то амплитуда передаваемого импульса принимается равной разрешенному значению, являющемуся ближайшим, к истинному. Такое преобразование называется квантованием, совокупность разрешенных значений амплитуд передаваемых импульсов – шкалой квантования, а интервал между соседними разрешенными значениями – шагом квантования.
Квантование приводит к ошибке квантования (шум квантования) E(t)=Z(t) – v(t). Квантование при передаче сигналов, во–первых позволяет применить импульсно – кодовую модуляцию и, следовательно, использовать все преимущества, обеспечиваемые ею, во – вторых представляет собой мощное средство борьбы со случайными помехами.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 1100; Нарушение авторских прав?; Мы поможем в написании вашей работы!