Привязка сетевого графика к календарю и построение масштабных сетевых графиков

После того как параметры модели рассчитаны, в рамках планирования проекта возникает необходимость назначить событиям и работам конк­ретные даты и представить график в более наглядной и привычной форме, доступной для использования на любом уровне управления, задать для графика масштаб времени. Дальнейшие работы по оптимизации исполь­зования ресурсов, таких как персонал, машины и механизмы, невозмож­ны без привязки графика к календарю, так как у каждого ресурса суще­ствует свой календарь использования.

Сначала осуществляется привязка событий и работ к календарю с помо­щью календарной линейки (таблица 15).

Таблица 15 - Календарная линейка

Рабочие дни графика

Рабочие дни месяца

1 неделя

2 неделя

3 неделя

Месяц

Год

Например, раннее начало какой-либо работы равно 2. Отыскиваем эту цифру в верхней части линейки, где указаны рабочие дни графика. Под этой цифрой внизу стоит цифра 3. Это означает, что раннее начало данной работы с 3-го числа месяца (например, с 3 апреля). Раннее оконча­ние этой же работы равно 7, т.е. эта работа должна заканчиваться к 10-му числу того же месяца (10 апреля).

При использовании календарной линейки следует иметь в виду, что «начало» работ определяется «с такой-то даты», а «окончание» — «к такой-то дате».

В календарную линейку вносятся календарные дни, во время которых производятся работы (рабочие дни), т.е. выходные и праздничные дни исключаются. Иногда календари различных ресурсов не совпадают. Но на данном этапе это не имеет особого значения: проблема решается в рамках подсистемы управления ресурсами проекта.

После определения календарных сроков, соответствующих ранним и поздним началам и окончаниям работ, можно построить масштабный сете­вой график, привязанный (или не привязанный) к календарю.

Построение масштабных сетевых графиков осуществляется на масштаб­ной (календарной) сетке времени в основном по ранним свершениям событий. При этом продолжительность каждой работы находится как расстояние между центрами двух событий, определяющих эту работу в проекции на горизонтальную ось времени.

Место каждого события на масштабной сетке определяется точкой оконча­ния самой продолжительной входящей в него работы. Все остальные входящие в это событие работы соединяются с ним линией в виде пружины или волнистой линией со стрелкой на конце. Таким образом, «пружинистой» или волнистой линией изображается частный резерв времени работы.

Зависимости, идущие на масштабном сетевом графике с наклоном впра­во, изображаются линией в виде разорванной пружины или пунктирно­волнистой линией со стрелкой на конце.

В качестве исходной модели для построения масштабного сетевого графи­ка используем несложный сетевой график (рисунок 32). Его параметры пред­ставлены в таблице 16.

5

10

2

3 8

6

7

Рисунок 32 - Исходная модель для построения масштабного сетевого графика

Таблица 16 - Параметры модели, представленной на рисунке 32

h-i	i	j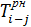
-
		-		-			-		-	-

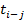
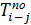
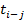
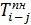
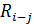
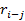
Теперь на основе этих данных построим масштабный сетевой график (рисунок 33).

20

Рисунок 33 - Масштабный сетевой график

По масштабному графику без проведения каких-либо дополнительных расчетов можно определить все параметры сетевого графика. Например, по графику видно, что = 2, 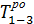– 7 (окончание участка стрелки в виде сплошной прямой линии), 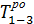= 14 (окончание пружины), 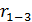= 7 (длина пружины) и т.д. Если сопоставить эти данные с результатами табличного расчета этого графика (см. таблицу 16), то можно убедиться в абсолютной идентичности параметров графика. Критический путь — это путь без пру­жин (волнистых линий). Часто для удобства контроля за продолжительностью выполнения работ временной ряд делают двойным — сверху в прямом порядке, а снизу — в обратном. Это позволяет определять, сколько времени прошло от начала проекта и сколько осталось до его завершения (рисунок 34).

20

24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Рисунок 34 - Масштабный сетевой график с двойным временным рядом (прямым и обратным)

Привязка рассматриваемого масштабного сетевого графика к календарю показана на рисунке 35.

20

1 2 3 4 5 8 9 10 11 12 15 16 17 18 19 22 23 24 25 26 29 30 2 3 4

Апрель Май

2013 год

Рисунок 35 - Привязка масштабного сетевого графика к календарю

Тесты и задания

Выберите один или несколько правильных ответов

1. Потенциал события — это:

а) максимальное время от данного события до завершающего события;

б) минимальное время от начального события до данного;

в) разность полного и частного резерва данного события;

г) разность полного и частного резерва данного события, деленная на продолжительность критического пути;

д) длина максимального пути, проходящего через данное событие, деленная на длину критического пути.

2. Если продолжительность работы увеличить на величину частного ре­зерва времени, то продолжительность критического пути:

а) увеличится на величину частного резерва;

б) не изменится;

в) увеличится в два раза.

3. К подкритическим можно отнести работы, коэффициент напряжен­ности которых:

а) ≤ 0,6;

б) 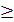0,8;

в) = 1.

4. У многоцелевых сетей может быть:

а) одно завершающее событие;

б) два завершающих событий;

в) более одного завершающего события;

г) ни одного завершающего события.

5. У многоцелевых сетей может быть:

а) один критический путь;

б) более одного критического пути;

в) ни одного критического пути.

6. Стохастическими можно назвать сетевые модели:

а) работы которых имеют вероятностную продолжительность;

б) все события которых обязательно произойдут;

в) некоторые события которых имеют вероятностную характеристику.

7. Детерминированными можно назвать сетевые модели:

а) все события которых обязательно произойдут;

б) некоторые события которых имеют вероятностную характеристику.

8. Рассчитывать сетевые графики с вероятностной продолжительностью работ позволяет методика:

а) СРМ;

б) РЕRТ;

в) GЕRТ.

9. Вероятностная продолжительность работы характеризуется:

а) средним значением;

б) дисперсией;

в) модой;

г) медианой;

д) средним геометрическим отклонением.

10. Расчет средней продолжительности работы осуществляется исходя из:

а) одной оценки;

б) двух оценок;

в) трех оценок.

11. При вероятностной оценке продолжительности всего проекта рассчитываются:

а) средняя продолжительность критического пути;

б) стандартное нормальное отклонение продолжительности критического пути;

в) среднее квадратическое отклонение продолжительности критического пути.

12. Проблемы, возникающие при использовании методов РЕRТ, заклю­чаются в том, что:

а) при разных значениях дисперсии продолжительности работ критический путь может меняться, что приводит к изменению мно­гих параметров сетевого графика;

б) для корректного использования методов необходимо большое количество критических работ;

в) продолжительности работ не всегда имеют β-распределения.

13. Масштабный сетевой график — это:

а) сетевой график, построенный в масштабе времени;

б) сетевой график, масштаб которого равен средней продолжительности выполнения критических работ;

в) сетевой график, привязанный к календарю.

14. Рассчитайте представленный сетевой график. Определите:

1) работы, составляющие критический путь;

2) подкритические работы, если подкритическими считать работы с резервом строго менее 5 дней;

3) подкритические работы, если подкритическими считать работы с резервом не более 5 дней.

4

2 1

2 5 5 4 3

1 8

3 5

15. Определите для представленного сетевого графика:

1) коэффициенты напряженности работ;

2) подкритические работы при условии, что к подкритическим относятся работы, коэффициент напряженности которых больше 0,6;

3) резервные работы при условии, что к резервным работам относятся работы, коэффициент напряженности которых меньше 0,5.

4

5

2 2 6 4

5 2 7 9

1 2 4

7

16. Рассчитайте представленный многоцелевой сетевой график. Резуль­таты занесите в приведенную ниже таблицу.

8

2 4 3

5 8

h-i	i	j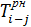
		-
		-

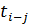
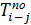
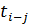
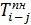
17. Рассчитайте представленный многоцелевой сетевой график. Резуль­таты занесите в приведенную ниже таблицу.

5 4

7

10 8

i	j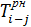
	-
	-

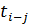
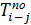
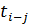
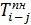
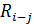
18. Рассчитайте представленный многоцелевой сетевой график. Резуль­таты занесите в приведенную ниже таблицу.

10

2 4 1

1 3

6

3

4 5

i	j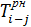
	-
	-
	-

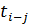
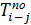
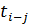
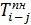
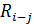
Дата добавления: 2014-12-17