Табличный метод расчета аналитических параметров сетевой модели 4 страница

3 Дополнительные методы расчета сетевых моделей

3.1 Подкритические работы

Как уже говорилось, полный резерв времени работы равен разности между длиной критического пути и максимальной длиной пути, который проходит через данную работу. Поэтому полный резерв времени является как бы мерой критичности работы: чем меньше полный резерв, тем бли­же к критическому пути максимальный по длине путь, проходящий че­рез данную работу. Зная полные резервы, можно определить работы, лежащие на путях, отличающихся по длине от критического пути не более чем на заданную величину. Такие работы принято называть подкритическими.

При управлении проектом внимание руководства должно быть сосредоточено в первую очередь на критических работах. Однако и подкритические работы, т.е. работы, имеющие небольшие резервы времени, следует дер­жать под постоянным контролем, особенно в продолжительных проектах.

Для каждого проекта или для всех проектов, осуществляемых в рамках одной программы, необходимо определить величину отклонения от критического пути δ, определяющую диапазон подкритических работ. Однозначно принятых значений этой величины не существует.

Таким образом, если задана величина отклонения от критического пути δ, то все работы, полный резерв которых не превосходит δ, будут подкритическими. Эти работы образуют подкритические пути, длина 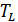которых удовлетворяет неравенству

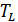- δ ≤ ≤ (11)

После определения подкритических работ необходимо выявить подкрити­ческие пути, т.е. пути, на которых лежат подкритические работы. Это удобно сделать на сетях, в кружках событий которых представлены номе­ра предшествующих событий, через которые проходят максимальные пути.

Выявление критических и подкритических работ проекта можно осуще­ствлять с помощью коэффициента напряженности. Для этого устанавли­вается величина коэффициента напряженности, которая определяет, ка­кие работы относить к подкритическим. Затем рассчитываются коэффи­циенты напряженности всех работ и формируются так называемые зоны подкритических работ. К критическим работам относят работы с коэф­фициентом напряженности, равным единице, т.е. К_н = 1, а к подкритиче­ским — работы с коэффициентом, удовлетворяющим условию 0,8 ≤ К_н < 1. Иногда выделяют резервные работы, у которых К_н ≤ 0,6.

Выделение этих трех разновидностей работ необходимо в больших и про­должительных проектах, когда руководителю проекта сложно контролировать все важные составляющие проекта и необходимо разделить ответ­ственность между руководителем и его заместителями или непосредствен­ными подчиненными.

3.2 Расчет многоцелевых сетевых моделей

В практике проектного управления приходится решать задачи по управлению несколькими проектами одновременно либо сложными многоцелевыми проектами и программами. Особенность использования сетевых моделей в многоцелевом проектном управлении состоит в том, что необ­ходимо строить и рассчитывать многоцелевые сетевые модели.

Правила построения многоцелевых сетевых графиков в основном совпа­дают с общими правилами построения сетевых моделей. Единственное отличие состоит в том, что допускается существование нескольких завершающих событий. При построении многоцелевых сетевых графиков не­обходимо следить за тем, чтобы под видом завершающих событий в графике не оказались тупиковые, ошибочные события.

Расчет многоцелевого сетевого графика осуществляется аналогично расчету одноцелевого графика. Для этого применимы любые методы расчета аналитических параметров из представленных выше.

Рассчитаем табличным методом многоцелевой сетевой график, приведенный на рисунке 29. Единственной особенностью при этом будет являться то, что в таблице окажется несколько строк конечных событий, т.е. строк, где в графах 3, 5, 10 и 11 будут проставлены прочерки. Таких строк будет столько, сколько конечных целей будет содержать график.

1

2 5

4

3 6

4

Рисунок 29 - Многоцелевой сетевой график

Результаты расчета графика представлены в таблице 12.

Таблица 12 - Расчет многоцелевого сетевого графика табличным методом

h-i	i	j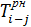
-
		-		-			-		-	-
		-		-			-		-	-

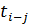
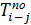
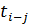
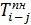
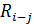
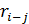
Как видно из таблицы, события 4—5 являются конечными событиями сети.

В многоцелевом сетевом графике будет столько критических путей, сколь­ко завершающих событий. В графике, представленном на рис. 29, два критических пути. Они отмечены на рисунке 30.

Один критический путь соединяет начальное событие с первым заверша­ющим событием, в нашем случае — с событием 4. Этот критический путь проходит через события 0—1—4 и составляет три дня.

Второй критический путь соединяет начальное событие со вторым завершающим событием — с событием 5. Этот критический путь проходит через события 0—1—2—5 и составляет 17 дней.

Участок, совпадающий с работой 0—1, для обоих критических путей явля­ется общим.

1

2 5

4

3 6

4

Рисунок 30 - Критические пути многоцелевого сетевого графика

Многоцелевые проекты и программы требуют дополнительных усилий по управлению. По сути, это уже не один, а два проекта, которые влияют друг на друга. Поэтому вместо одной системы управления в многоцелевых проектах возникает три — две на каждый из проектов, которые в данном случае выступают уже как подпроекты, и одна общая.

3.3 Сетевые модели с вероятностной оценкой продолжительности работ

При расчете аналитических параметров сетевого графика (см. выше) предполагалось, что время выполнения каждой работы точно известно. В боль­шинстве проектов соблюдение этого условия невозможно. Управление проектом направлено на достижение уникальной цели, что предполагает планирование и реализацию сложных комплексов работ, чаще всего не имевших в прошлом никаких аналогов. В советское время для определе­ния продолжительности работ использовались разного рода нормы и пра­вила. В настоящее время этой системы нормирования не существует: она была разрушена в ходе экономических реформ, к тому же взрывной харак­тер технологических изменений во многих отраслях народного хозяйства потребовал новых подходов к определению продолжительности работ. Поэтому при реализации современных проектов необходимо использовать сетевые модели с вероятностной оценкой продолжительности работ.

Такие модели не следует путать со стохастическими (вероятностными) сетевыми моделями, так как сетевые модели с вероятностной оценкой продолжительности работ являются детерминированными. Детерминированные сетевые модели — сетевые модели, события которых не имеют вероятностной характеристики, т.е. обязательно свершаются и свершают­ся в установленной последовательности, хотя продолжительность работ может иметь вероятностную оценку.

Вместе с тем встречаются проекты, в которых тот или иной комплекс последующих работ зависит от не известного заранее результата. Напри ­ мер, может быть предусмотрено несколько вариантов продолжения ис­следования в зависимости от полученных опытным путем данных или несколько вариантов строительства предприятий различной мощности по обработке сырья в зависимости от результатов разведки запасов этого сырья. Такого рода сетевые модели называются стохастическими. Стохастические сети, так же как и детерминированные, могут характеризовать ­ ся детерминированными либо случайными продолжительностями работ.

Конечно, и при построении сетевых моделей с вероятностной оценкой продолжительности работ и при построении стохастических сетевых мо­делей мы имеем дело с одним и тем же явлением — с неопределенностью. Таким образом, стохастические модели отличаются от детерминированных по структуре, а не по вероятности или детерминированности продолжительностей работ. Поэтому следует правильно использовать устоявшу­юся терминологию.

Рассматриваемые здесь методы были первоначально разработаны в рам­ках методики РЕRТ.

Рассмотрим несложный математический аппарат этих методов и проде­монстрируем, как его использовать при расчете параметров сетевых моде­лей в условиях вероятностной оценки продолжительности работ и проекта в целом.

При расчете сетевых моделей методом РЕRТ продолжительность работ является случайной величиной, подчиняющейся собственному закону рас­пределения, а значит, обладающей собственными числовыми характери­стиками. Такими характеристиками являются средняя продолжительность работы 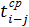и дисперсия оценки продолжительности работы (дисперсия работы) .

Значения 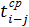и рассчитываются при допущении, что распределение продолжительностей работ обладает тремя свойствами:

· непрерывностью;

· унимодальностью (наличием единственного максимума у кривой распределения);

· конечностью и неотрицательностью диапазона возможных значений продолжительности (кривая распределения имеет две точ­ки пересечения с осью ОХ, абсциссы которых неотрицательны).

Исходными данными для расчетов служат экспертные оценки продолжительностей работ:

· оптимистическая оценка 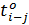, т.е. оценка продолжительности работы i—j при благоприятных условиях;

· пессимистическая оценка 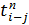, т.е. оценка продолжительности работы i—j при неблагоприятных условиях;

· наиболее вероятная оценка , т.е. оценка продолжительности работы i—j при нормальных условиях.

Средняя продолжительность 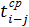и дисперсия оценки продолжительности каждой отдельной работы определяются по следующим формулам:

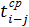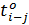= ( + 4 + 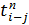): 6; (12)

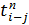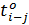= [( - ): 6]². (13)

Бывают случаи, когда наиболее вероятное время выполнения работы оценить сложно. Поэтому в реальных проектах часто используется упрощен­ная (и, естественно, менее точная) оценка средней продолжительности работы, которая определяется на основе двух задаваемых временных оценок — оптимистической и пессимистической:

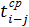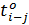= (2 + 3 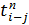): 5. (14)

При расчете средней продолжительности работы по формуле (14) диспер­сию следует определять по-другому:

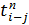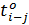= [( - ): 5]². (15)

или

= 0,04(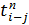 - 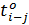)². (16)

Средняя продолжительность работы представляет собой наиболее веро­ятную продолжительность работы. Дисперсия является мерой диапазона возможных значений продолжительности, или мерой разброса оценок. Если дисперсия велика, это означает, что и неопределенность продолжи­тельности выполнения работ велика. (Иными словами, различные значе­ния продолжительности имеют почти равную вероятность.) Если диспер­сия мала, это означает, что неопределенность продолжительности выпол­нения работы мала, т.е. время выполнения работы определено более или менее точно. Работа, не лежащая на критическом пути, но облада­ющая большей дисперсией, чем критическая работа, может превратить­ся в критическую работу и существенно изменить весь сетевой график проекта.

В качестве примера рассмотрим две работы а и b, по которым получены экспертные оценки, приведенные в таблице 13.

Таблица 13 - Экспертные оценки продолжительности работ

Оценка	Работа
а	b
Оптимистическая
Наиболее вероятная		5,5
Пессимистическая

Используя формулу (12), найдем средние продолжительности этих работ:

= (4 + 4 × 6 + 8): 6 = 6;

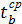= (5 + 4 × 5,5 + 9): 6 = 6.

Как видим, средние продолжительности этих работ равны, хотя их опти­мистические, наиболее вероятные и пессимистические оценки отличают­ся. Поскольку разница между пессимистической и оптимистической оцен­кой этих работ одинакова, дисперсия их оценки, рассчитываемая по фор­муле (13), также будет одинаковой:

= [(8 - 4): 6]² = 0,44;

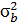= [(9 - 5): 6]² = 0,44.

Несколько изменим экспертные оценки продолжительностей работ (таблица 14).

Таблица 14 - Экспертные оценки продолжительности работ

Оценка	Работа
а	b
Оптимистическая
Наиболее вероятная
Пессимистическая

Средние продолжительности обеих работ останутся без изменения:

= (4 + 4 × 6 + 8): 6 = 6;

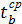= (5 + 4 × 6 + 7): 6 = 6.

Но изменится дисперсия, так как изменился (уменьшился) диапазон воз­можных значений продолжительности работы b:

= [(8 - 4): 6]² = 0,44;

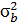= [(7 - 5): 6]² = 0,11.

Дисперсия работы b в четыре раза меньше дисперсии работы а. Это озна­чает, что вероятность завершения работы b в 6 дней в четыре раза выше, чем вероятность завершения в этот же срок работы а.

Вероятностные характеристики продолжительности отдельных работ ис­пользуются для определения параметров всего проекта в целом. Когда средняя продолжительность (и прочие показатели) проекта рассчитывается с помощью уже известных алгоритмов, только при этом в качестве продолжительности работ используется средняя продолжительность. Значения всех аналитических параметров сетевого графика — длины критического пути, определяющего продолжительность всего проекта, и ранних и поздних свершений событий, резервов событий и работ — будут такими же, как если бы мы использовали не среднюю, а обыкновенную продолжительность работ. Но при этом необходимо понимать, что по своей сути все эти парамет­ры будут являться средними значениями соответствующих случайных величин.

Обобщенной вероятностной оценкой продолжительности всего проекта является средняя длина критического пути сетевого графика, которая вычисляется как сумма всех средних продолжительностей работ, лежащих на критическом пути:

= . (17)

Ожидаемая продолжительность выполнения проекта (средняя продолжительность критического пути сетевого графика проекта) может оказаться неприемлемой. Тогда вместо нее выбирается директивная продолжитель­ность и возникает необходимость оценить вероятность того, что про­ект завершится не позднее директивно установленного срока.

Для решения этой задачи необходимо:

· определить среднее квадратическое (стандартное) отклонение длины критического пути (формула (18));

· рассчитать аргумент функции Лапласа (интеграла вероятностей) Z (формула (19));

· найти значение функции Лапласа Ф (Z) (по таблицам стандартно­го нормального распределения (таблицам значения интеграла вероятностей));

· вычислить вероятность соблюдения директивных сроков выполнения проекта Р ( ≤ ) (формула (20)).

Формулы для определения названных величин:

= ; (18)

Z = ( - ): ; (19)

P ( ≤ ) = Ф (Z). (20)

где 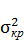— дисперсия работы, лежащей на критическом пути.

Рассчитаем сетевой график, представленный на рисунке 31, методом РЕRТ.

9 3

6 8 5

8 4 10 3 4 5 13 6 13

3 6 8 4 17

9

9 719106

Рисунок 31 - Сетевой график для расчета методом РЕRТ

Критический путь этого сетевого графика (см. рисунок 31) составляют рабо­ты 0—3, 3—5, 5—6, 6—9, 9—10, 10—11. Допустим, на графике над работа­ми проставлены средние их продолжительности, а дисперсии работ, со­ставляющих критический путь, следующие:

= 2,5;

= 2,1;

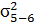= 3,2;

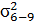= 4,0;

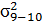= 1,5;

= 3,5.

Оценим вероятность выполнения проекта в срок при , равном 63 дням. Найдем среднее квадратическое отклонение длины критического пути:

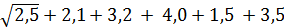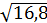= = ≈ 4,1.

Рассчитаем значение аргумента функции Лапласа:

Z = (63 - 61): 4,1 ≈ 0,49.

Обратившись к таблице значений функции стандартного нормального распределения (можно воспользоваться функцией программы Мiсrоsоft Ехсеl НОРМСТРАСП()), определим Ф(Z):

Ф(Z) = Ф(0,49) = 0,6879.

Что и будет искомой вероятностью P ( ≤ 63).

Таким образом, вероятность того, что проект, сетевой график которого представлен на рисунке 31, с учетом введенных значений дисперсий критических работ завершится не позднее 63 дней, составляет около 0,6879.

В практике управления проектами возникает необходимость решения и обратной задачи, т.е. определения максимального срока выполнения проекта с заданной вероятностью (с заданной надежностью). Продолжитель­ность выполнения проекта при таких условиях может быть найдена следующим образом:

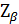= + × , (21)

где 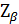— аргумент функции Лапласа, соответствующий значению функции, рав­ному β, т.е. Ф(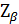) = β (определяется по той же таблице стандартного нормального распределения).

Рассчитаем возможный срок выполнения проекта, сетевой график кото­рого представлен на рисунке 31, с заданной надежностью β = 0,95.

Найдем аргумент функции Лапласа, соответствующий значению 0,95 (мож­но воспользоваться таблицей стандартного нормального распределения или же формулой НОРМСТОБР () в программе Мiсrоsоft Ехсеl. Он равен — 1,6449. По формуле (21) определяем:

= 61 + 1,6449 × 4,1≈ 68 дней.

При заданной вероятности 0,95 наш проект завершится за 68 календарных дней.

Дата добавления: 2014-12-17