Табличный метод расчета аналитических параметров сетевой модели 1 страница

Существует большое количество алгоритмов расчета сетевых графиков как ручным, так и автоматизированным способом. Любой программный пакет по календарному планированию проекта (например, МS Рrоjесt, Тiте Linе, Spider, ОрепРLап, Рrimavera Suretrackи др.) позволяет рассчитать аналити­ческие параметры любого сетевого графика. Но знание «ручных» техно­логий позволяет лучше понять взаимосвязь между этими показателями и использовать сетевые модели без каких-либо специализированных программ.

Итак, рассчитаем параметры сетевой модели табличным методом. Восполь­зуемся тем же сетевым графиком, на примере которого мы рассчитывали аналитические параметры в предыдущих параграфах (см. рисунок 28). Для этого воспользуемся таблицей 2.

Таблица 2 - Таблица для расчета аналитических параметров сетевой модели

h-i	i	j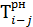

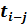
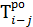
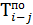
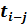
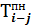
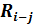
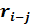
В графу 1 вносится количество работ, предшествующих рассчитываемой, в графу 2 — номера начальных событий рассчитываемых работ, в гра­фу 3 — номера конечных событий рассчитываемых работ, в графу 4 — ранние начала работ, в графу 5 — продолжительности выполнения работ, в графу 6 — ранние окончания работ, в графу 7 — поздние окончания работ, в графу 8 — продолжительности выполнения работ, в графу 9 — поздние начала работ, в графу 10 — общие резервы работ, в графу 11 — частные резервы работ.

Графы 1, 2, 3, 5 и 8 заполняются данными из сетевого графика. Затем сверху вниз заполняются графы в таком порядке: 4 и 6, 7 и 9, 10, 11.

1. Определим 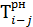и 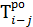для работ 0—1 и 0—2.

В графу 4 запишем нули, так как работы 0—1 и 0—2 выходят из исходного события графика. Графа 6 равняется сумме значений граф 4 и 5 (таблица 3).

Таблица 3 - Раннее начало и раннее окончание работ 0—1 и 0—2

h-i	i	j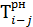
-
-

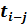
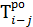
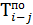
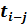
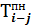
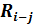
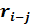
2. Определим 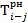и 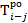для работ 1—2 и 1—3 (таблица 4).

Таблица 4 - Раннее начало и раннее окончание работ 1—2 и 1—3

h-i	i	j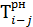
-
-
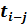
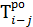
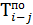
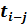
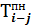
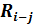
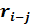
					5
					7

Значение графы 4 определяем следующим образом. В графе 1 по строке работы 1—2 проставлена цифра 1. Это означает, что работе 1—2 предше­ствует одна работа, т.е. если событие 1 искать сверху в графе 3, то оно встретится всего один раз. По строке найденного события (работа 0—1) отыскиваем значение графы 6, которое равно 2. Эту цифру переносим в графу 4 по строке работ 1—2 и 1—3 (так как обе работы выходят из одного и того же события и, следовательно, имеют одно и то же раннее начало), после этого определяем графу 6.

3. Определим 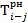и 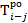для работ 2—3 и 2—4 (таблица 5).

Таблица 5 - Раннее начало и раннее окончание работ 2—3 и 2—4

h-i	i	j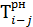
-
-

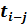
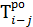
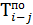
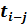
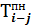
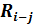
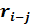
В графе 1 по строке работы 2—3 стоит цифра 2. Событие 2 встретится в графе 3 сверху от определяемой строки дважды. Событие 2 находится в строках работ 0—2 и 1—2. По этим строкам отыскиваем значения гра­фы 6, они равны 6 и 5 соответственно.

Исходя из формулы (2) максимальное значение — 6 переносим в графу 4 по строкам работ 2—3 и 2—4.

4. Определим 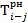и 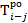для всех остальных работ аналогичным образом (таблица 6).

Таблица 6 - Раннее начало и раннее окончание всех работ

h-i	i	j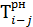
-
-

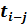
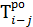
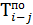
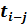
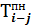
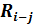
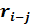
5. Для определения граф 7 и 9 нужно правильно заполнить еще одну — последнюю строку таблицы (таблица 7).

Таблица 7 - Таблица со строкой завершающего события

h-i	i	j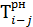
-
-
		—		—			-		—	—

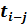
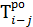
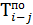
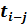
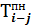
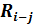
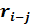
Как видим, в графе 3 стоит прочерк. Это означает, что в этой строке со­держатся не параметры работы, а параметры события.

Известно, что событие не имеет продолжительности (прочерки в графах 5 и 8), а завершающее событие не имеет также и резервов (прочерки в гра­фах 10 и 11). Следовательно, для завершающего события в графах 4, 6, 7 и 9 должна быть проставлена одна и та же величина — 24.

6. Определим 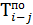и 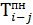для работ 4—5, 3—5, 3—4 и 2—4 (таблица 8).

Таблица 8 - Позднее окончание и позднее начало работ 4—5, 3—5, 3—4 и 2—4

h-i	i	j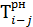
-
-
		—		—			-		—	—

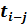
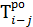
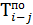
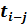
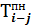
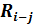
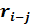
Расчет граф 7 и 9 осуществляется снизу вверх. Берем номер события из графы 3 (для работы 4—5 это будет событие 5). Затем отыскиваем это событие в графе 2 снизу от определяемой работы (4—5). По строке найденного события отыскиваем значение графы 9. Оно равно 24. Эту цифру за­писываем в графу 7 по строкам работ 4—5 и 3—5 (так как обе работы входят в одно и то же событие и, следовательно, имеют одну и ту же величину позднего окончания). После этого определяем значение графы 9 по работам 4—5 и 3—5, которое равно разнице значения графы 7 и значения графы 8.

7. Определим 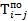и 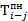для всех оставшихся работ (таблица 9).

Таблица 9 - Позднее окончание и позднее начало всех работ

h-i	i	j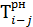
-
-
		—		—			-		—	—

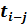
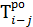
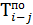
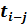
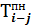
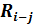
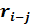
Находим событие 3 в графе 3 по строке работы 2—3. Затем отыскиваем это же событие внизу от определяемой работы (2—3) в графе 2. Здесь оно встречается дважды, в строках 3—4 и 3—5.

По строкам этих работ отыскиваем значение графы 9 и выбираем мини­мальное, которое и записываем в графу 7 по строкам работ 2—3 и 1—3.

Затем определяем значение графы 9. Аналогично определяются значения граф 7 и 9 и по всем остальным работам.

8. Определим 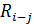для каждой работы.

Значения графы 10 получаются в результате вычитания по каждой строке значений графы 6 из значений графы 7. По строкам критических работ (0—2, 2—3, 3—5) в графе 10 записываются нули (таблица 10).

Таблица 10 - Полный резерв времени работ сетевого графика

h-i	i	j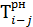
-
-
		—		—			-		—	—

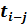
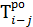
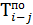
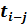
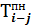
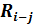
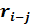
9. Определим 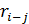для каждой работы.

Значение графы 11 рассчитывается как разность раннего начала (графа 4) и раннего окончания данной работы (графа 6). Работы, не имеющие обще­го резерва, не имеют и частного резерва, поэтому в графе 11 ставят 0 везде, где 0 имеется в графе 10 (таблица 11).

Таблица 11 - Частный резерв времени работ сетевого графика

h-i	i	j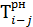
-
-
		—		—			-		—	—

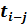
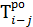
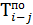
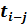
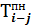
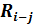
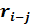
Частный резерв может быть найден и иным способом. У всех работ, обла­дающих нулевым полным резервом, частный резерв будет равен нулю. В нашем примере это работы 0—2, 2—3, 3—5. Таким образом, в графе 11 по строкам этих работ ставится 0. Затем находятся некритические работы, у которых конечное событие в графе 3 встречается один раз. По строкам этих работ в графе 11 ставится также 0. В нашем примере это будет работа 0—1. В строках работ, которые имеют завершающее событие в графе 3 более одного раза, в графе 11 ставится значение разницы между макси­мальным ранним окончанием этих работ и ранним окончанием данной работы. У работы, которая имеет максимальное раннее окончание, част­ный резерв будет равен 0. Так, в нашем примере событие 2 в графе 3 встречается дважды. По строкам этих событий отыскиваем значения гра­фы 6. Они равны 6 и 5. По строке максимума, т.е. по строке работы 0—2, в графе 11 получаем 0, по строке работы 1—2 в графу 11 записываем результат разницы чисел 6 и 5, т.е. 1. Аналогично определяется графа 11 и по всем остальным строкам.

Дата добавления: 2014-12-17