
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение ранних начал и ранних окончаний работ сетевой модели
|
|
|
|
Ранние начала и ранние окончания работ сетевой модели определяют последовательно, слева направо по графику, т.е. от исходного события сети к завершающему.
Произведем расчет параметров графика, изображенного на рисунке 28.
2 10
6 6
Рисунок 28 - Сетевой график для расчета аналитических параметров
Для всех работ, выходящих из исходного события сети, раннее начало всегда равно нулю, т.е.:
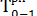 = 0;
= 0;
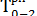 = 0.
= 0.
Прежде чем определить величину раннего начала для всех последующих работ, необходимо определить раннее окончание работ, выходящих из исходного события сети. Раннее окончание для всех работ сетевого графика будет равно сумме раннего начала работы и ее продолжительности, т.е.:
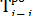 =
= 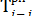 +
+ 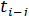 . (1)
. (1)
Для работ 0—1 и 0—2 ранние окончания будут равны 2 и 6 дней соответственно:
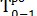 = 0 + 2 = 2;
= 0 + 2 = 2;
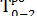 = 0 + 6 = 6.
= 0 + 6 = 6.
Если раннее окончание работы 0—1 равно 2, то могут ли работы 1—2 и 1—3 начинаться раньше, чем закончится работа 0—1? Очевидно, нет. Все работы, следующие за работой 0—1, могут начинаться только после самого раннего окончания работы 0—1, т.е. эта величина и есть раннее начало работ 1—2 и 1—3:
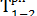 =
= 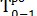 ;
;
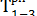 =
= 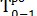 .
.
Другими словами, раннее начало данной работы равно раннему окончанию предшествующей работы. Ранние начала работ 1—2 и 1—3 будут равны:
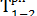 = 2;
= 2;
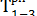 = 2.
= 2.
Таким образом, работы, выходящие из исходного события, имеют одно и то же раннее начало — начало, равное нулю. Работы, выходящие из события 1, имеют ранее начало 2. Очевидно, что все работы, которые выходят из одного и того же события, всегда имеют одно и то же раннее начало. Определив раннее начало для одной работы, мы можем записать то же значение раннего начала абсолютно для всех работ, выходящих из того же события, что и данная работа.
Используя формулу (1), определим раннее окончание работ 1—2 и 1—3:
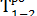 =
= 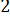 + 3 = 5;
+ 3 = 5;
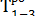 = 2 + 5 = 7.
= 2 + 5 = 7.
Далее определим раннее начало работ 2—3 и 2—4. Напомним, что сложное событие свершается только тогда, когда все работы, в том числе и самая длительная, завершаются. Для работы 2—3 предшествующими работами являются 1—2 и 0—2, которые имеют ранние окончания 5 и 6 соответственно. Раннее начало работы 2—3 будет определяться наибольшим из ранних окончаний предшествующих работ, т.е. будет равно 6. Таким образом, раннее начало для всех работ можно определить по формуле
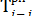 = max
= max 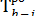 , (2)
, (2)
т.е. раннее начало данной работы равно максимальному из ранних окончаний непосредственно предшествующих ей работ.
Используя формулы (1) и (2), определим раннее начало и раннее окончание для всех остальных работ сетевого графика (см. рисунок 28):
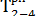 = 6 (так же, как и у работы 2—3);
= 6 (так же, как и у работы 2—3);
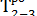 = 6 + 8 = 14;
= 6 + 8 = 14;
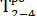 = 6
= 6 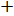 7 = 13;
7 = 13;
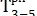 = max
= max 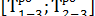 = 14.
= 14.
Напомним, что логическая зависимость является полноправным элементом расчета параметров сети:
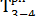 = 14 (так же, как и у работы 3—5);
= 14 (так же, как и у работы 3—5);
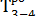 = 14 + 0 = 14;
= 14 + 0 = 14;
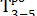 = 14 + 10 = 24;
= 14 + 10 = 24;
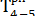 = max
= max 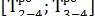 = 14;
= 14;
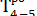 = 14 + 6 = 20.
= 14 + 6 = 20.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 942; Нарушение авторских прав?; Мы поможем в написании вашей работы!