Правила построения сетевых моделей

Единой последовательности построения сетевой модели (сетевого графика) нет. Поэтому строить модели можно по-разному — двигаясь от начала проекта (исходного события) к его окончанию (завершающему событию), и наоборот — от окончания к началу. Более логичным и правильным сле­дует признать метод построения графиков от исходного события к завершающему, т.е. слева направо, так как при таком построении четко просле­живается технология выполнения моделируемых работ.

В качестве первого правила сетевого моделирования следует указать правило последовательности изображения работ: сетевые модели следует строить от начала к окончанию, т.е. слева направо.

Правило изображения стрелок. В сетевом графике стрелки, обозначаю­щие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны идти слева направо, не отклоняясь влево от оси орди­нат, и всегда направляться от предшествующего события к последующе­му, т.е. от события с меньшим порядковым номером к событию с большим порядковым номером.

Правило пересечения стрелок. При построении сетевого графика следует избегать пересечения стрелок: чем меньше пересечений, тем нагляднее график.

Правило обозначения работ. В сетевом графике между обозначениями двух смежных событий может проходить только одна стрелка.

В практике зачастую встречаются случаи, когда две и более работы начи­наются одним и тем же событием, выполняются параллельно и заканчива­ются одним и тем же событием. Например, одновременно начинается про­ектирование двух вариантов конструкции новой машины (работы а и б), после чего проводится сопоставление и выбор лучшего варианта (рабо­та в). Изображение этих работ на сетевом графике не должно выводить две работы из одного события и завершать их одним и тем же событием (рисунок 16а), так как в этом случае две работы получат одно и то же обозна­чение — 1—2. Это недопустимо, потому что при расчете сетевого графика невозможно будет определить параметры этих работ и параметры всего сетевого графика.

Для правильного изображения работ можно ввести дополнительное собы­тие и зависимость (рисунок 16б). Теперь работы а и б имеют уникальные числовые обозначения — 1—3 и 1—2 соответственно, и никаких трудно­стей при расчете параметров сетевого графика не возникнет.

а

в а в

б б

а) б)

Рисунок 16 - Неверное изображение параллельно выполняемых работ (а), распараллеливание работ в сетевой модели (б)

Правило расчленения и запараллеливания работ. При построении сете­вого графика можно начинать последующую работу, не ожидая полного завершения предшествующей. В этом случае нужно «расчленить» предшествующую работу на две, введя дополнительное событие в том месте предшествующей работы, где может начаться новая.

Например, необходимо корректировать рабочие чертежи (работа а, про­должительность 30 дней) и изготовить испытательный стенд (работа б, продолжительность 25 дней). Если эти работы изобразить последователь­но, то их общая продолжительность составит 55 дней (рисунок 17а ). Соста­вив сетевой график и еще раз проанализировав взаимосвязи между рабо­тами, приходим к выводу, что работу б можно начать уже после того, как будет выполнена половина работы а, т.е. через 15 дней. Закончить же работу б можно только после полного завершения работы а. Исходя из этого можно построить новый сетевой график (рисунок 17б). Как видно из рисунка, общая продолжительность работ теперь составляет 42 дня, т.е. получается выигрыш во времени продолжительностью в 13 дней.

а) а - 15 б - 25 а

б) а₁ - 15 а₂ - 15

б₁ - 13 б₂ - 12

Рисунок 17 - Последовательное изображение работ (а),

расчленение и запаралле­ливание работ (б)

Правило запрещения замкнутых контуров (циклов, петель). В сетевой модели недопустимо строить замкнутые контуры — пути, соединяющие некоторые события с ними же самими, т.е. недопустимо, чтобы один и тот жепуть возвращался в то же событие, из которого он вышел.

На рисунке 18а продемонстрирован сетевой график, в котором можно обнаружить замкнутый контур: работы 1—3, 3—2 и 2—1 образуют петлю. Начиная движение от события 1 и двигаясь по направлению стрелок, можно попасть снова к событию 1. Это недопустимо.

Рисунок 18б показывает, что при наличии пересечений обнаружить кон­туры труднее. Но, тем не менее, двигаясь по стрелкам, видим, что в данном случае замкнутый контур принял форму «восьмерки», объединяющей со­бытия 1, 3, 2 и 4: путь вернулся к исходному событию. Такое изображение также недопустимо.

а) б)

Рисунок 18 - Неправильное построение сетевой модели: а) замкнутый контур в виде петли; б) замкнутый контур

Если в модели образовался замкнутый контур, это значит, что имеются ошибки в технологии выполнения работ или в составлении графика (вспомните правило изображения стрелок).

Правило запрещения тупиков. В сетевом графике не должно быть тупи­ков, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события (в многоцелевых графиках завершающих собы­тий несколько, но это особый случай) (рисунок 19а).

Правило запрещения хвостовых событий. В сетевом графике не должно быть хвостовых событий, т.е. событий, в которые не входит ни одна работа, за исключением начального события (рисунок 19б).

а) б)

Рисунок 19 - Неправильное построение сетевой модели; а) наличие тупика; б) наличие хвостового события

Правило изображения дифференцированно-зависимых работ. Если одна группа работ зависит от другой группы, но при этом одна или несколько работ имеют дополнительные зависимости или ограничения, при построении сетевого графика вводят дополнительные события.

Допустим, есть две группы работ — а, б, в и г, д, е (рисунок 20а). Представим, что существует следующая зависимость между этими группами: работа г зависит от работ б и в, а работа д зависит только от работы б. Сетевая модель, объединяющая обе группы работ, которая приведена на рисунке 20б, не верна, так как сетевой график показывает, что работа д зависит как от работы б, так и от работы в, а это противоречит исходной моделируемой технологии.

а)

а в г е

б д

б)

а в г е

б д

в)

в г

а е

бд

Рисунок 20 - Две группы зависимых работ (а). Неправильное (б) и правильное (в) изображение зависимых работ в одной сетевой модели

Чтобы построить правильную сетевую модель, необходимо ввести допол­нительное событие. Правильный сетевой график показан на рисунке 20в. В нем работы г и д являются дифференцированно-зависимыми и каждая имеет свою зависимость от предшествующих работ.

Правило изображения поставки. В сетевом графике поставки (под постав­кой понимается любой результат, который предоставляется «со стороны», т. е. не является результатом работы непосредственного участника проек­та) изображаются двойным кружком либо другим знаком, отличающимся от знака обычного события данного графика. Рядом с кружком поставки дается ссылка на документ (контракт или спецификацию), раскрывающий содержание и условия поставки.

Пример изображения поставки приведен на рисунок 21а. Но бывают и более сложные случаи.

Например, на рисунке 21б показана поставка, входящая в событие 2. Судя по графику, поставка необходима сразу для двух работ — 2—3 и 2—4. Но если нужно изобразить, что поставка требуется для работы 2—4, сле­дует применить правило изображения дифференцированно-зависимых работ, т.е. ввести дополнительное событие (2') и зависимость (2—2') (рисунок 21в). Поставка теперь необходима только для работы 2'—4, что со­ответствует производственной технологии.

а)

б)

в)

2'

Рисунок 21 - Изображение поставки: а) для одной работы; б) для двух работ; в) для одной из работ, выходящих из одного события

Правило учета непосредственных примыканий (зависимостей). В сете­вом графике следует учитывать только непосредственное примыкание (зависимость) между работами.

Так, на рисунке 22 показано несколько работ: а, б, в и г. Работе г предшест­вует только работа в. Если нужно показать, например, что работе г пред­шествует также работа а, то это надо сделать специально вводимой зави­симостью (см. рисунок 22).

а б в г

Рисунок 22 - Изображение непосредственных зависимостей работ

Технологическое правило построения сетевых графиков. Для построения сетевого графика необходимо в технологической последовательности ус­тановить:

· какие работы должны быть завершены до начала данной работы;

· какие работы должны быть начаты после завершения данной работы;

· какие работы необходимо выполнять одновременно с выполне­нием данной работы.

Как было уже сказано, работа обозначается номерами начального и ко­нечного событий — события, из которого работа выходит (i), и события, в которое работа входит (j), т.е. работа ограничена событиями i и j. Рабо­та, предшествующая данной, обозначается как h—i, а последующая — как j—k. Время выполнения данной работы обозначается как 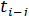,предшеству­ющей работы — , последующей работы — _.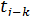

Это правило изображено на рисунке 23.

Например, необходимо выполнить работы а, б, в, г, д и е. Работы а и б начинаются одновременно. Работа г должна выполняться после работ б и в, работа в — после работы а, работа д — после работы а, работа е — после работ г и д.

Эту технологическую последовательность выполнения работ запишем в табличной форме (рисунок 23а).

Предшествующие работы (h-i)	Данные работы (i-j)
- - а б, в а г, д	а б в г д е

а)

б)

а в д

б г е

Рисунок 23 - Сетевой график (б), построенный на основе данных таблицы (а)

Начнем построение сетевого графика.

1. Работам а и б другие работы не предшествуют.

2. Работа в должна выполняться после работы а.

3. Окончание работы в объединяем с окончанием работы б, так как следующая работа – г должна выполняться после работы б, а работа г – после окончания работ б и в.

4. Работа д выполняется после работы а.

5. Окончание работы д объединяем с окончанием работы г, так как следующая работа – е должна выполняться после окончания работ г и д.

График построен.

Важнейшим вопросом построения сетевых графиков, безусловно, является четкое определение всех взаимосвязей между работами в их технологической последовательности. В сетевом графике нельзя допускать никаких отклонений от моделируемой технологии, так как малейшее нарушение может привести к неадекватности создаваемой модели.

Только после точного определения всех взаимосвязей и последовательности работ можно приступить к построению сетевого графика.

Правила кодирования событий сетевого графика. Для кодирования сете­вых графиков необходимо пользоваться следующими правилами.

1. Все события графика должны иметь свои собственные номера.

2. Кодировать события необходимо числами натурального ряда без пропусков.

3. Номер последующему событию следует присваивать после присвоения номеров предшествующим событиям.

4. Стрелка (работа) должна быть всегда направлена из события с меньшим номером в событие с большим номером.

Последовательность проставления цифр в кружки событий определяется нумерацией событий и направленностью стрелок (рисунок 24а).

Четкая система кодирования позволяет выявить имеющиеся в сети замк­нутые контуры.

Например, при кодировке сети, изображенной на рисунке 24б, обнаружива­ется замкнутый контур.

а) б)

Рисунок 24 - Нумерация событий в сети (а) и выявление замкнутого контура (б)

Дата добавления: 2014-12-17