
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обобщенный метод наименьших квадратов
|
|
|
|
В общем случае ковариационная матрица  может быть любой симметричной положительно определенной матрицей.
может быть любой симметричной положительно определенной матрицей.
Для исследования модели в общем случае (в частности, при наличии гетероскедастичности либо автокорреляции) используется так называемый обобщенный метод наименьших квадратов (сокращенно ОМНК).
Изложим этот метод.
Основные гипотезы общей линейной регрессионной модели.
1)  (1)
(1)
2)  (2)
(2)
3)  , где (3)
, где (3)
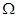 – симметричная положительно определенная матрица размера
– симметричная положительно определенная матрица размера 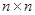
4)  (4)
(4)
Поскольку 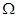 симметричная положительно определенная матрица, обратная матрица
симметричная положительно определенная матрица, обратная матрица  также симметрична и положительно определена. Следовательно, существует такая симметричная положительно определенная матрица
также симметрична и положительно определена. Следовательно, существует такая симметричная положительно определенная матрица 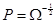 , что
, что
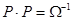 (5)
(5)
В частности, если 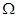 диагональная (случай гетероскедастичности):
диагональная (случай гетероскедастичности):
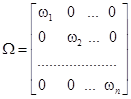 (6)
(6)
то
 (7)
(7)
и матрица 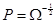 имеет вид:
имеет вид:
 (8)
(8)
Можно показать, что
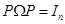 (9)
(9)
Умножим (1) слева на  :
:
 (10)
(10)
Обозначим:
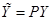 ,
, 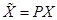 ,
, 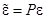 (11)
(11)
В силу (11) равенство (10) можно записать:
 (12)
(12)
В силу (2) и (11):
 .
.
Следовательно,
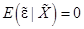 (13)
(13)
В силу (3), (9), (11)

Следовательно,
 (14)
(14)
Если отклонения 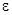 распределены нормально (при условии
распределены нормально (при условии  ), то и
), то и 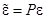 также распределены нормально (при условии
также распределены нормально (при условии  ).
).
Следовательно, для модели (12) выполнены условия классической линейной регрессионной модели. Поэтому все результаты, полученные для классической регрессионной модели, справедливы и для модели (12).
В соответствии с формулой для МНК-оценок коэффициентов регрессии для модели (12) в силу (5):
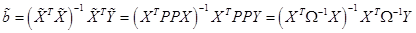 . (15)
. (15)
Итак, МНК-оценка для модели (5):
 (16)
(16)
Эта оценка называется ОМНК-оценкой для исходной модели (1).
Как следует из результатов для классической модели, ОМНК-оценка 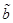 является несмещенной и эффективной линейной оценкой вектора коэффициентов
является несмещенной и эффективной линейной оценкой вектора коэффициентов  .
.
В силу (5) в соответствии с формулой для ковариационной матрицы оценок коэффициентов  для классической модели:
для классической модели:

Итак,
 (17)
(17)
Обозначим:
 (18)
(18)
 (19)
(19)
прогнозные значения и соответствующие остатки для исходной модели с использованием 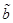 .
.
Обозначим:
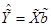 (20)
(20)
 (21)
(21)
прогнозные значения и соответствующие остатки для новой модели.
В соответствии с формулой (3.32):
 (21’)
(21’)
В соответствии с результатами для классической модели случайные векторы 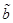 и
и  независимы.
независимы.
В соответствии с формулой (3.34):
 (21’’)
(21’’)
В соответствии с формулой (3.35) для классической модели необъясненная дисперсия для новой модели равна:
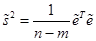 (22)
(22)
Величина 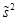 является несмещенной оценкой параметра
является несмещенной оценкой параметра 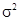 .
.
Как следует из результатов для классической модели:
 (22’)
(22’)
В силу (11), (18)-(22):
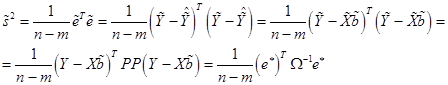
Итак, величина 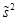 может быть найдена по формуле:
может быть найдена по формуле:
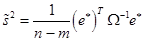 (23)
(23)
Обозначим:
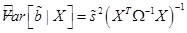 , (39)
, (39)
В силу несмещенности оценки 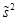 из (24) следует, что матрица (39) является несмещенной оценкой ковариационной матрицы векторной МНК-оценки
из (24) следует, что матрица (39) является несмещенной оценкой ковариационной матрицы векторной МНК-оценки 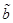 .
.
Заметим, что элементы главной диагонали матрицы 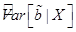 – оценки
– оценки 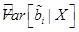 дисперсий коэффициентов
дисперсий коэффициентов  . Следовательно, величины:
. Следовательно, величины:
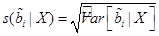 (40)
(40)
можно считать оценками стандартных отклонений коэффициентов  .
.
При выполнении гипотезы (4) величины:
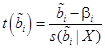 (41)
(41)
являются t -статистиками для новой модели, и, следовательно, имеют распределение Стъюдента с  степенями свободы.
степенями свободы.
Поэтому, в соответствии с результатами для классической модели доверительные интервалы для коэффициентов  определяются из равенства:
определяются из равенства:
 , (42)
, (42)
где 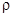 – уровень значимости, а
– уровень значимости, а 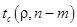 – соответствующая двусторонняя квантиль распределения Стъюдента с числом степеней свободы
– соответствующая двусторонняя квантиль распределения Стъюдента с числом степеней свободы  .
.
В силу (41), (42) интервальные оценки для коэффициентов  имеют вид:
имеют вид:
 (43)
(43)
Проверка гипотезы: 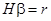
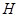 – матрица размером
– матрица размером  ,
,  ,
, 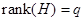 ,
,
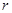 – вектор-столбец длиной
– вектор-столбец длиной  .
.
В соответствии с результатами для классической модели, при выполнении гипотезы:
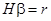 (44)
(44)
величина:
 (45)
(45)
имеет распределение Фишера (F -распределение) с  степенями свободы:
степенями свободы:
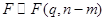 (46)
(46)
Поскольку в силу (5), (11)
 (47)
(47)
статистика (45) может быть записана в виде:
 (48)
(48)
Отметим, что в силу формулы (39) формулу (48) можно также записать в виде:
 (48’)
(48’)
Напомним, что при выполнении гипотезы (44) имеет место равенство:
 , (49)
, (49)
где 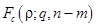 –
– 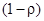 -квантиль распределения Фишера с
-квантиль распределения Фишера с  степенями свободы.
степенями свободы.
В случае, если  нулевая гипотеза отвергается; если
нулевая гипотеза отвергается; если  , нет оснований отвергать нулевую гипотезу (и она принимается).
, нет оснований отвергать нулевую гипотезу (и она принимается).
Доверительная область для коэффициентов регрессии
Рассмотрим случай, когда  .
.
Тогда равенство (44) примет вид: 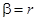
Заменив 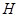 на
на 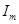 и
и 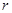 на
на  в формуле (48), получим:
в формуле (48), получим:
 (50)
(50)
Отметим, что в силу формулы (39) формулу (50) можно также записать в виде:
 (50’)
(50’)
В силу (49), (50) 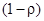 -доверительная область для вектора
-доверительная область для вектора  задается условием:
задается условием:
 (51)
(51)
и является эллипсоидом в m -мерном пространстве.
С учетом (50’) условие (51) можно записать виде:
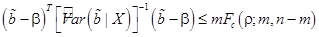 (51’)
(51’)
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 496; Нарушение авторских прав?; Мы поможем в написании вашей работы!