Типовые задачи курса ТАУ

Использования пакета MATHCAD иллюстрирует решение типовых задач первой части курса ТАУ, посвященной линейным САУ. Ниже рассматривается построение годографов характеристического уравнения и АФЧХ, графиков амплитудно-частотных характеристик (АЧХ), фазо-частотных характеристик (ФЧХ), логарифмических АЧХ и ФЧХ, решение задач устойчивости по критериям Гурвица, Михайлова, Найквиста, а также построение переходного процесса.

Построение годографа АФЧХ.

Построение годографа АФЧХ и АЧХ графиков вещественной и мнимой частотных характеристик включает следующие этапы:

-формирование параметров анализируемой передаточной функции:

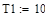
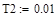
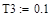
-формирование выражения анализируемой передаточной функции:

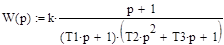
-формирование линейного частотного диапазона:

-построение графика вещественной частотной характеристики:

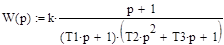
-построение графика мнимой частотной характеристики:

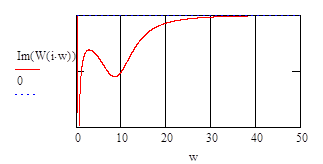
-корректировка частотного диапазона для более точного построения годографа АФЧХ:

Или с шагом 0,01

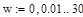
- построение графика годографа АФЧХ:

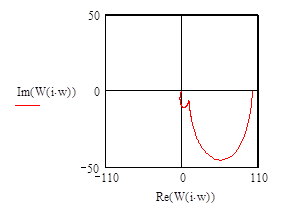
Текст соответствующего MATHCAD файла приведен в приложении 1.

Построение логарифмических АФЧХ.

Построим логарифмические АЧХ и ФЧХ для примера, используемого в разделе 2.1.

Основной проблемой при построении логарифмических АЧХ и ФЧХ является задание декадно-логарифмического частотного диапазона, например: 1,2,3,…,9,10,20,30,…,90,100,200,…

Эта проблема решается следующим образом.

Задаются параметры частотного ряда:

w0:= 0.01 – начальная частота ряда;

n:= 4 – количество декад;

i:=1…n – ряд декад;

j:=1…9 – ряд частотного поддиапазона (декады);

Выражение для декадно-логарифмического частотного диапазона приводится ниже:

В результате вычислений формируется следующий частотный ряд:

0.01,…,0.09 0.1,…,0.9 1,…,9 10,…,90

или

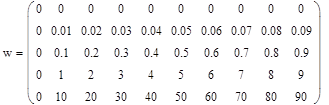
Далее формируется известное [1-5] математическое выражение логарифмической амплитудно-частотной характеристики:

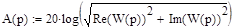
В данном случае p является формальным параметром выражения.

Строится график логарифмической АЧХ:

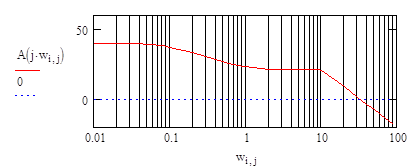
Далее формируется известное [1-5] математическое выражение логарифмической фазо-частотной характеристики:

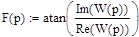
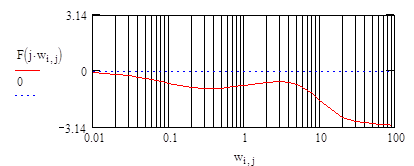
и непосредственно строится график логарифмической ФЧХ:

 

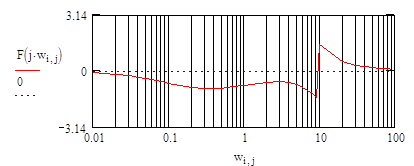
Следует отметить наличие разрыва графика при достижении абсциссой величины

–π / 2, что обусловлено областью определения арктангенса [–π / 2, π / 2].

Для построения непрерывного графика логарифмической ФЧХ необходимо сместить разрыв на – π, применяя функцию arg, тогда выражение примет вид:

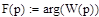
Текст MATHCAD файла, реализующего построение логарифмических АЧХ и ФЧХ приведен в приложении 2.

Построение годографа характеристического уравнения.

В качестве примера рассмотрим характеристическое уравнение, заданное следующим выражением:

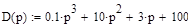
Для частотного диапазона w:=0,0.01…7 построим годограф характеристического уравнения:

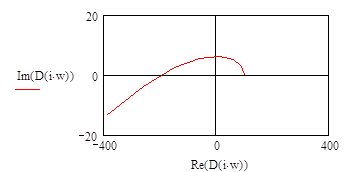
Текст MATHCAD файла, реализующего построение годографа характеристического уравнения, приведен в приложении 3.

Определение устойчивости.

Критерий устойчивости ГУРВИЦА.

Использование MATHCAD при определении устойчивости САУ по критерию ГУРВИЦА требует знания команд формирования и редактирования матриц.

Рассмотрим процедуру использования MATHCAD при анализе следующего характеристического уравнения:

Для формирования шаблона определителя ГУРВИЦА сформируем матрицу, нажав клавиши [Alt]+[M]. Командная строка потребует определения количества столбцов и строк. Задав размер матрицы: 6 6, получим следующий шаблон определителя ГУРВИЦА:

Полученный шаблон матрицы ГУРВИЦА заполняется согласно известному правилу [1-5] следующим образом:

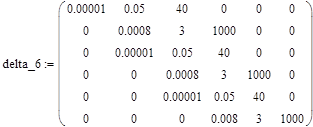
Далее согласно правилу [1-5], необходимо вычислить все главные миноры определителя ГУРВИЦА. Для удобства и простоты общения с MATHCAD, вычислим все миноры, начиная со старшего.

Для вычисления определителя матрицы delta_6 необходимо сформировать символ определителя, нажав клавишу [ | ], и заполнить его именем матрицы delta_6. Получим следующий результат:

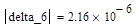
Для вычисления следующего минора delta_5 необходимо скопировать матрицу delta_6 ниже, используя клавиши [F2], [F4], и изменить имя минора на delta_5.

Чтобы удалить лишние в этом случае нижнюю строку и правый столбец, необходимо маркер подвести к нижнему правому элементу 1000 и нажать клавиши [Alt]+[M]. Командная строка потребует пояснения для удаления (что будет означать знак -) или дополнения (знак +) текущей матрицы. Необходимо набрать -1 -1 и будет удалена нижняя строка и правый столбец. Выражение примет следующий вид:

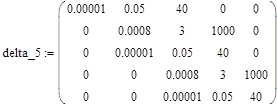
Вычислим минор delta_5 приведенным ниже образом:

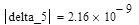
Аналогично составляются и вычисляются остальные миноры определителя ГУРВИЦА:

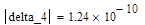
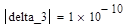
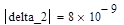
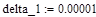
После анализа знаков и величин всех диагональных миноров принимается заключение об устойчивости САУ [1-5].

Полный текст MATHCAD файла, реализующего анализ устойчивости САУ по критерию Гурвица, приведен в приложении 4.

Критерий устойчивости Михайлова.

Использование пакета MATHCAD при решении задачи устойчивости САУ по критерию Михайлова заключается в построении годографа в комплексной плоскости [1-5]. Рассмотрим эту задачу на следующем примере, описанном в разделе 4.2.1.

Дано характеристическое уравнение САУ:

Пусть частотный диапазон для анализа:

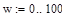
Построим годограф Михайлова в комплексной плоскости:

Проанализируем поведение годографа Михайлова [1-5]:

-начинается на положительной вещественной полуоси;

-вращается против часовой стрелки относительно начала координат;

-последовательно обходит 5 квадрантов.

Следовательно анализируемая САУ устойчива.

Полный текст MATHCAD файла, реализующего анализ устойчивости САУ по критерию Михайлова, приведен в приложении 5.

Критерий устойчивости Найквиста.

Задача определения устойчивости замкнутой САУ базируется на анализе поведения годографа АФЧХ в комплексной плоскости.

Исследуем устойчивость замкнутой САУ, передаточная функция которой в разомкнутом состоянии имеет следующее выражение:

Пусть частотный диапазон анализа:

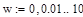
Строим годограф АФЧХ разомкнутой САУ в комплексной плоскости:

Анализ поведения годографа АФЧХ показывает, что замкнутая САУ устойчивая, т.к. при отсутствии положительных вещественных корней АФЧХ разомкнутой САУ не охватывает точку с координатами (-1,-j0).

Полный текст MATHCAD файла, реализующего анализ устойчивости САУ по критерию Найквиста, приведен в приложении 6.

Выделение областей устойчивости в плоскости одного

варьируемого параметра.

Задание: Определить допустимые вариации параметра К для системы, заданной следующей структурной схемой.

Зададим выражения передаточных функций:

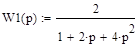
Определим выражение комплексного коэффициента усиления К интегрирующего звена в цепи отрицательной обратной связи в следующем виде:

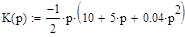
Построим фигуративную линию комплексного коэффициента усиления при

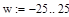
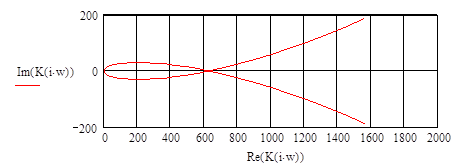
Определим точку пересечения фигуративной линии с вещественной положительной осью путем использования функций нахождения корней следующим образом:

Переменная первого приближения решения:

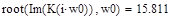
-корень уравнения.

Результат получен с точностью до третьего знака, что задано конфигурацией MATHCAD.

Дальнейшая штриховка фигуративной линии и выделение областей устойчивости выполняется согласно известным правилам [1-5].

Полный текст MATHCAD файла, реализующего анализ устойчивости САУ в плоскости одного варьируемого параметра 7.

Построение кривой переходного процесса.

Решение задачи построения кривой переходного процесса основывается на известной взаимосвязи вещественной частотной характеристики и переходного процесса.

Построим график кривой переходного процесса для следующей передаточной функции простейшего колебательного звена:

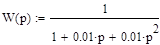
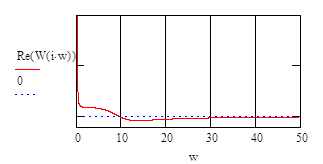
Проанализируем график вещественной частотной характеристики для частотного диапазона w:=0..100

Анализ показывает, что вещественная частотная характеристика постоянно имеет значения очень близкие к 0, начиная с частоты 30 рад/сек. Следовательно ограничимся рассмотрением именно этого частотного диапазона для построения кривой переходного процесса.

Итак, частотный диапазон w:=0..30.

Найдем значение вещественной части на нулевой частоте так как эта величина есть значение переходного процесса в установившемся режиме.

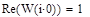
Построим график вещественной части характеристики для последнего частотного диапазона:

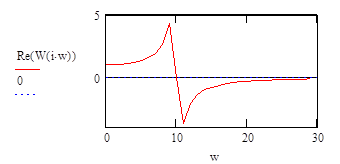
Опишем известную [1-5] взаимосвязь вещественной частотной характеристики и кривой переходного процесса:

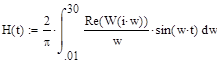
Зададим временной диапазон анализа:

Последним этапом является непосредственное построение кривой переходного процесса

Полный текст MATHCAD файла, реализующего построение кривой переходного процесса САУ, приведен в приложении 8.

Дата добавления: 2014-12-17