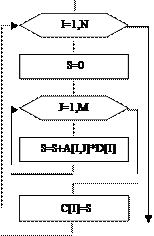КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи для самостоятельной работы 1 страница
|
|
|
|
Раздел "Циклы" 1-й уровеь.
1. Дано натуральное число n. Вычислить
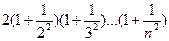
2. Дано натуральное число n. Вычислить

3. Даны действительное число а, натуральное число n.

4 Вычислить. Число корней n задано.
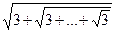
5. Вычислить

6. Даны действительные числа х, а, натуральное число n. Вычислить

7. Дано действительное число а. Найти среди чисел
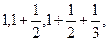 первое, больше а
первое, больше а
8. Даны натуральное n, действительное x. Вычислить
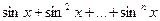
9. Даны натуральное n, действительное x. Вычислить.
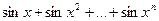
10. Дано натуральное число n. Сколько цифр в числе n?
11. Дано натуральное число n. Чему равна сумма его цифр?
12. Дано натуральное число n. Найти первую цифру числа n.
13. Даны натуральные числа n,m. Получить сумму m последних цифр числа п.
14. Дано натуральное число n. Выяснить, входит ли цифра 3 в запись числа n2.
15. Дано натуральное число n. Поменять порядок цифр числа n на обратный.
16. Дано натуральное число n. Переставить первую и последнюю цифры числа n.
17. Даны натуральное числа m и n, m = > n. Используя алгоритм Эвклида, найти наибольший общий делитель m и n.
18. Пусть x1 =y1 = 1; xi = 0.3 xi-1; yi=xi-1+yi-1; i=2,3,... Дано натуральное число n. Найти
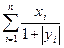
19. Пусть a1=b1=1; ak=3bk-1+2ak-1; bk=2ak-1+bk-1; k= 2,3,... Дано натуральное n. Найти

20. Пусть x1=x2=x3=1; xi=xi-1+xi-3, i = 4,5,...100, найти
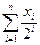
21. Даны положительные действительные числа а,х,е. В последовательности у1,у2,..., образованной по закону
 i=1,2,…
i=1,2,…
найти первый член yn, для которого выполнено неравенство 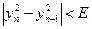
22. Пусть
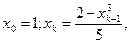 k=1,2,…
k=1,2,…
найти первый член xn, для которого 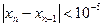
23. Дано целое число m > 1. Получить наибольшее целое k, при котором 4k < m
24. Дано натуральное число n. Получить наименьшее число вида 2k, превосходящее n.
25. Дано натуральное число n. Вычислить 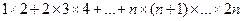
26. Дано натуральное число n. Вычислить

27. Для заданного натурального n вычислить:
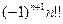
где n!! означает  для нечетного n и
для нечетного n и 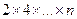 для четного n.
для четного n.
28.Вычислить

29. Вычислить
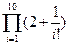
30 Дано натуральное число n. Вычислить
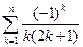
31Дано натуральное число n. Вычислить
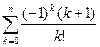
32Даны натуральное число n, действительное число x. Вычислить

ЗЗ. Даны натуральное число n, действительное число x. Вычислить

34. Дано натуральное число n. Вычислить произведение первых n сомножителей
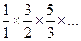
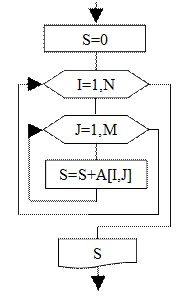 Рис. 7.1
Схема алгоритма
суммирования
элементов массива
Рис. 7.1
Схема алгоритма
суммирования
элементов массива
|
 Рис. 7.2
Схема алгоритма суммирования
диагональных элементов матрицы
Рис. 7.2
Схема алгоритма суммирования
диагональных элементов матрицы
|
 Рис. 7.3
Схема алгоритма суммирования
элементов строк матрицы
Рис. 7.3
Схема алгоритма суммирования
элементов строк матрицы
|  Рис. 7.4
Схема алгоритма суммирования
двух матриц
Рис. 7.4
Схема алгоритма суммирования
двух матриц
|
35.Вычислить

следующими четырьмя способами:
а) последовательно слева направо;
б) последовательно слева направо вычисляются отдельно суммы
слагаемых, стоящие на нечетных и четных местах, а затем второе значение вычитается из первого;
в) последовательно справа налево;
г) аналогично п.б., только справа налево.
Почему при вычислениях на ЭВМ каждым из этих способов получаются разные результаты?
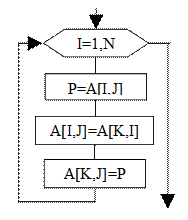 Рис. 7.5
Схема алгоритма
перестановки 1-й
и k-й строк матрицы А
Рис. 7.5
Схема алгоритма
перестановки 1-й
и k-й строк матрицы А
| 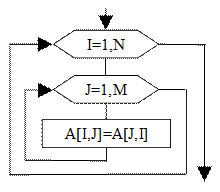 Рис. 7.6
Схема алгоритма
транспонирования
матрицы А
Рис. 7.6
Схема алгоритма
транспонирования
матрицы А
|
 Рис. 7.7
Схема алгоритма
удаления k-й строки
матрицы А
Рис. 7.7
Схема алгоритма
удаления k-й строки
матрицы А
|
 N=N+1
Рис. 7.8
Схема алгоритма
включения k-й строки
матрицы А
N=N+1
Рис. 7.8
Схема алгоритма
включения k-й строки
матрицы А
|
Раздел "Циклы" 2-ой уровень
1. Даны натуральные числа n, а1,...аn. Определить количество членов ak последовательности а1,...аn, являющихся квадратами четных чисел.
2. Даны натуральные числа n, а1,...аn. Определить количество членов ak последовательности а1,...аn, удовлетворяющих условию 2k < аk <k!
3. Даны натуральные числа n, а1,...аn. Определить количество членовАк последовательности а1,...аn, имеющихчетные порядковые номера и являющихся нечетными числами.
4. Даны натуральные числа n, а1,...аn. Найти те члены Ai последовательности а1,...аn, которые при делении на 7 дают остаток 1,2 или 5.
5. Даны натуральное число n, целые числа а1,...аn. Найти количество и сумму тех членов данной последовательности, которые делятся на 5 и не делятся на 7.
Рис. 7.9 Схема алгоритма преобразования матрицы А в одномерный массив Х
|
НЕТ
Рис. 7.10 Схема алгоритма поиска минимального элемента матрицы А | ||||||||||||||||||||||||||||||||||||||||||
ПЕЧАТЬ С
Рис. 7.11 Схема алгоритма умножения матрицы на вектор
|
ПЕЧАТЬ Рис. 7.12 Схема алгоритма умножения матрицы на матрицу |
6. Даны натуральные числа n,р, целые числа а1,...аn. Получить произведение членов последовательности а1,...аn, кратных р.
7. Даны натуральное число n, действительные числа x1,...,xn. В последовательности x1,...,xn все члены, меньшие двух, заменить нулями. Кроме того, получить сумму членов, принадлежащих отрезку [3,7], а также число таких членов.
8. Дано натуральное число n, действительные числа а1,...аn. В последовательности а1,...аn все неотрицательные члены, не принадлежащие отрезку [1,2], заменить на единицу. Кроме того, получить число отрицательных членов и число членов, принадлежащих отрезку [1,2].
9. Дано натуральное число n, целые числа а1,...аn. Заменить все большие семи члены последовательности а1,...аn числом 7. Вычислить количество таких членов.
10. Даны натуральное число n, целые числа а, х1,...,xn. Если в последовательности х1,...,xn есть хотя бы один член, равный а, то получить сумму всех членов, следующих за первым таким членом; в противном случае ответом должно быть число 100.
11. Даны натуральное число n, b0,...,bn. Вычислить
f(b0) +f(b1)+...+f(bn), где
f(x) = х 2, если х кратно 3,
f(x)=x, если х при делении на 3 дает остаток 1,
f(x) = [х/3], в остальных случаях
12. Даны целые числа а, n, х1,...,xn (n > 0). Определить каким по счету идет в последовательности х1,...,xn член, равный а. Если такого члена нет, то ответом должно быть число 0.
13. Даны натуральное число n, действительные числа а1,...,an. Получить min (а2,а4,...) + max (al,a3,...).
14. Даны натуральное число n, действительное число х. Среди чисел
 , k=1,...,n
, k=1,...,n
найти ближайшее к какому-нибудь целому.
15.Дано натуральное число n, действительные числа а1,...,an-Получить все натуральные i (2 < = i < = n-1), для которых
ai-1 < ai < ai+1.
16. Пусть xl=0.3; x2=-0.3; xi,=i+sin (Xi-2), i=3,4,... Среди х1,...,x20 найти ближайшее к какому-нибудь целому.
17. Пусть

Дано натуральное n. Среди а1,...,an найти все положительные числа, среди положительных а1,...,an выбрать наименьшее число.
18. Даны натуральное число n, действительные числа а1,...,an. В последовательности а1,...,an определить число соседств двух положительных чисел.
19.Рассматривается последовательность а1,...,a1000. Требуется определить, сколько членов последовательности с номерами 1,2,4,8,16,... имеют значение, меньшее, чем 0.25. При этом считать, что
Ak=sin2 (3k+5) - cos (k2 -15), k= 1,2,...,1000
20. Даны натуральное число n, действительные числа а1,...,an. В последовательности а1,...,an определить число соседств двух чисел разного знака.
21. Дано натуральное число n, действительные числа х1,...,хn. Найти xi, при xi, max (|al|,..., |аn|), где ai=xi, при |xi| <=2 и ai = 0,5 в противном случае;
22. Рассматривается последовательность а1,...,а1000. Требуется определить, сколько членов последовательности с номерами 1,2,4,8,16,... имеют значение, меньшее чем 0.75! При этом считать, что а1=0.01;
Ak=sin (k+Ak-1), k=2,...,1000.
23. Дано натуральное число n, действительные числа а1,...,an. В последовательности а1,...,an определить число соседств двух чисел одного знака, причем модуль первого числа должен быть больше модуля второго числа.
24 Дано натуральное число n. Получить все такие натуральные q, что п делится на q и не делится на q^3.
25 Даны натуральные числа m,n (m< >0, n< >0). Получить все их натуральные общие кратные, меньшие m n.
26Даны целые числа m,n (m=0, n=0). Получить все их общие делители (положительные и отрицательные).
27 Даны действительные числа х,у (х > 0,у> 1). Получить целое число К (положительное, отрицательное или равно нулю), удовлетворяющее условию уk-1 < = х < уk.
28Дано натуральное число п. Вычислить произведение первых n сомножителей
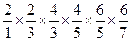
29.Даны натуральное число n, целые числа al,...,al0, bl,...,bl0, с1,...,с10. Верно ли, что отрицательный член в последовательности с1,...,с10 встречается раньше, чем в первых двух последовательностях.
30. Даны натуральное число n, действительные числа а1,...,an. Выяснить, образуют ли возрастающую последовательность числа al,...,an,2al,3a2,...,(n+ 1)an.
31. Дано натуральное число n. Можно ли представить его в виде суммы двух квадратов натуральных чисел? Если можно, то указать все пары х,у таких натуральных чисел, что n = х2 + у2, х > = у.
32. Даны натуральное число n, целые числа а1,...,an. Найти номер последнего нечетного члена последовательности а1,...,an. Предполагается, что такие члены в последовательности имеются.
РАЗДЕЛ "РАБОТА С МАССИВАМИ"
1. Дана действительная матрица A (N.M). Найти среднее арифметическое каждого из столбцов, имеющих четные номера.
2. Даны действительные числа х1,...,х8. Получить действительную квадратную матрицу порядка 8, где 1-я строка - все единицы, 2-я строка - х1,„.,х8, в последующих строках степень чисел х1,...,х8 увеличивается на 1 по сравнению с предыдущей.
3. Дана действительная матрица A (N.M). Определить числа b1,...,bn, равные соответственно разностям наибольших и наименьших значений элементов строк.
4. Дана действительная матрица A (N,M). Найти сумму наибольших значений элементов ее строк.
5. В данной действительной квадратной матрице порядка n найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.
6. В данной действительной матрице А (4,5) поменять местами строку, содержащую элемент с наибольшим значением, со строкой, содержащей элемент с наименьшим значением. Предполагается, что эти элементы единственны.
7. В данной квадратной целочисленной матрице порядка 5 указать индексы всех элементов с наибольшим значением.
8. Дана действительная матрица A (N.M), все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением, затем среди этих чисел выбирается наибольшее. Указать индексы элемента с найденным значением.
9. Дана действительная матрица A (N,M). Получить последовательность b1,...,bn, где bi - это произведение квадратов тех элементов i-й строки, модули которых принадлежат отрезку [1,1.5].
10. Дана целочисленная квадратная матрица порядка 5. Найти наименьшее из значений элементов столбца, который обладает наибольшей суммой модулей элементов. Если таких столбцов несколько, то взять первый из них.
11. Даны натуральное число n, целочисленная квадратная матрица порядка n. Получить b1,...,bn, где bi - это наименьшее из значений элементов, находящихся в начале i - строки матрицы до элемента, принадлежащего главной диагонали, включительно.
12. Дана целочисленная квадратная матрица порядка n. Получить b1,...,bn, где bi - это значение первого по порядку положительного элемента i-й строки (если таких элементов нет, то принять bi= 1).
13. Дана целочисленная квадратная матрица порядка n. Получить b1,...,bn, где bi - это сумма элементов, расположенных за первым отрицательным элементом в i-й строке (если все элементы строки неотрицательны, то принять bi= 100).
14. Дана целочисленная квадратная матрица порядка n. Получить b1,...,bn, где bi - это сумма элементов, предшествующих последнему отрицательному элементу i-й строки (если все элементы строки неотрицательны, то принять bi= -1).
15. Дана целочисленная квадратная матрица порядка n. Найти номера строк все элементы которых четные.
16. Дана действительная квадратная матрица порядка n. Построить последовательность действительных чисел а1,...,an по правилу: если в i-й строке матрицы элемент, принадлежащий главной диагонали, отрицателен, то ai равно сумме элементов i-й строки, предшествующих первому отрицательному элементу; в противном случае ai равно сумме последних элементов i-й строки, начиная с первого по порядку неотрицательного элемента.
17. Дана действительная квадратная матрица порядка 5. В строках с отрицательным элементом на главной диагонали найти наибольший из всех элементов.
18. Дана действительная квадратная матрица порядка n. Рассмотреть
те элементы, которые расположены в строках, начинающихся с отрицательного элемента. Найти суммы тех из них, которые расположены соответственно ниже, выше и на главной диагонали.
19. Дана действительная квадратная матрица порядка 5. Получить целочисленную квадратную матрицу того же порядка, в которой элемент равен единице, если соответствующий ему элемент исходной матрицы больше элемента, расположенного в его строке на главной диагонали, и
равен нулю в противном случае.
20. Дана целочисленная квадратная матрица порядка 5. Выяснить, имеются ли в матрице ненулевые элементы, и если имеются, то указать индексы всех ненулевых элементов.
21. Дана действительная квадратная матрица порядка 5. Вычислить сумму тех из ее элементов, расположенных на главной диагонали и выше нее, которые превосходят по величине все элементы, расположенные ниже главной диагонали. Если на главной диагонали и выше нее нет элементов с указанным свойством, то ответом должно служить сообщение об этом.
22. Дана вещественная матрица А (4,5). Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент (один из них) оказался в верхнем левом углу.
23. Дана вещественная матрица А (5,5). Вычислить
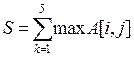
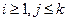
24.Дана -целочисленная квадратная матрица А (6,6). Заполнить массив А следующим образом:
1 2..6
7 8... 12
13 14... 18
…
31 32... 36
25. Дана целочисленная квадратная матрица А (6,6). Заполнить массив А следующим образом:
1 2…6
0 1...5
…
0 0... 1
26. Дана целочисленная матрица A (N,M). Определить количество "особых" элементов массива А, считая элемент "особым", если он больше суммы остальных элементов своего столбца.
27. Дана целочисленная матрица A (N.M). Определить количество "особых" элементов массива А, считая элемент "особым", если в его строке слева от него находятся элементы, меньшие его, а справа большие.
28. Дана вещественная матрица А (5,6). Упорядочить ее строки по неубыванию суммы их элементов.
29. Дана вещественная матрица А (5,6). Упорядочить ее строки по неубыванию их наибольших элементов.
30. Имеется таблица Т результатов некоторого шахматного турнира, в котором участвовало п шахматистов
Т: array [l..n,l..n] оf (В,Н,П,Х),
где Т (ij]=B, если i-й участник выиграл y j-го (при этом
Т [j,i] = П), Т [i,j] = Н, если i-й и j-й участники сыграли вничью, и
Т (i,i]=X. Возможный вид таблицы (при n=3):
ХВП
ПХН
ВНХ
за выигрыш дается 1 очко, за ничью - 0,5 очка, за проигрыш - 0 очков. Выдать на печать номера участников в порядке невозрастания набранных ими очков.
31. Преобразовать массив A (N.N), осуществив поворот элементов вокруг его центра на 90 против часовой стрелки.
32. Определить, является ли заданная целая квадратная матрица 6-го порядка симметричной (относительно главной диагонали.)
33. Говорят, что матрица имеет седловую точку Aij; если Aij является минимальным в i-й строке и максимальным bj'-m столбце. Найти номер строки и столбца какой-нибудь седловой точки заданной матрицы.
34. Дана вещественная матрица А (5,5), все элементы которой различны. Найти скалярное произведение строки, в которой находится наибольший элемент матрицы, на столбец с наименьшим элементом.
35. Начиная с центра, обойти по спирали (по часовой стрелке) все элементы квадратной матрицы А (7,7) распечатывая их в порядке обхода.
36. Начиная с верхнего левого угла, обойти по спирали (против часовой стрелки) все элементы квадратной матрицы А (7,7), распечатывая их в порядке обхода.
37. По заданной квадратной матрице А (10,10) построить вектор длиной 19, элементы которого - максимумы элементов диагоналей, параллельных главной диагонали.
38. Определить, является ли заданная целая квадратная матрица 9-го порядка магическим квадратом, т.е. такой, в которой суммы элементов во всех строках и столбцах одинаковы.
Варианты заданий к лабор.раб. 10 (5 ф)
ТЕМА: СТРОКИ. СИМВОЛЬНЫЕ МАССИВЫ.
1. Заданы натуральное число n, символы S1,..., Sn. Подсчитать: сколько раз среди заданных символов встречается символ " + " и сколько раз символ " * ".
2. Заданы символы S1,..., Sn. Известно, что среди символов S2, S3,... Sn есть несколько знаков вопроса. Определить количество символов пробела среди Si Sn, что следуют перед вторым знаком вопроса.
3. Заданы натуральное число n, символы S1,..., Sn. Получить первое натуральное i, для которого каждый из символов Si и Si+l совпадает с буквой "а".
4. Заданы натуральное число n, символы S1,..., Sn. Преобразовать последовательность S1,..., Sn, заменив в ней каждую точку тремя точками.
5. Заданы натуральное число n, символы S1,..., Sn. Исключить из данной последовательности все группы букв вида "abed".
6. Заданы натуральное число n, символы S1,..., Sn среди которых присутствует двоеточие. Получить все символы, которые расположены до первого двоеточия включительно.
7. Заданы натуральное число n, символы S1,..., Sn Посчитать наибольшее количество идущих подряд символов пробела.
8. Заданы натуральное число n, символы S1,..., Sn. Определить количестве вхождений в последовательность S1,..., Sn групп букв "abc".
9. Даны натуральное число n, символы Si,..., Sn. Найти кокое-нибудь слово, начинающееся буквой а и оканчивающееся буквой я (если таких слов нет, то необходимо сообщить об этом).
10. Даны натуральное число n, символы S1,..., Sn. Удалить из S1,..., Sn все слова с нечетными порядковыми номерами и перевернуть все слова с четными номерами.
11. Даны натуральное число n, символы S1,..., Sn. Удалить из S1,..., Sn,все слова, в которых встречается не более двух различных букв,
12. Даны натуральное число n, символы S1,..., Sn. Удалить из S1,..., Sn все слова, оканчивающиеся группой букв -кая или -кое.
13. Даны символы S1,..., Sn. Оставить последовательность S1,..., Sn без изменения, если в нее не входит символ *, иначе каждый символ /, предшествующий первому вхождению символа * заменить на запятую.
14. Даны символы S1,..., Sn. Оставить последовательность S1,..., Sn без изменения, если в нее входит символ *, иначе каждый символ./, предшествующий первому вхождению символа * удалить из последовательности.
15. Даны символы S1,..., Sn. Если последовательность S1,..., Sn „ является палиндромом, т.е. S1=Sn, S2=Sn-1, то оставить ее без изменения, иначе получить последовательность S1,..., Sn-1, Sn, Sn-1,S2,S1.
16. Дано натуральное число п. Сколько различных цифр встречается в его десятичной записи?
17. Проверить, является ли в заданном тексте баланс открывающих и закрывающих скобок.
18. В данном предложении указать слово, в котором доля гласных (А, Е, I, О) максимальна.
19. Для встречающихся в заданном тексте пар рядом расположенных символов указать, сколько раз встречается каждое из таких двухбуквенных сочетаний.
20. Отредактировать предложение; удаляя из него лишние пробелы, оставляя только по одному пробелу между словами.
21. Для каждого символа заданного текста указать сколько раз он встречается в тексте.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 2416; Нарушение авторских прав?; Мы поможем в написании вашей работы!






 ДА
ДА