
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модуль 5. Кратні, криволінійні та поверхневі інтеграли
|
|
|
|
КОНТРОЛЬНА РОБОТА № 2
Модуль 4. Диференціальні рівняння
4.1. Знайти загальний розв’язок (або загальний інтеграл) диференціальних рівнянь:
а) першого порядку з відокремлюваними змінними,
б) однорідного (першого порядку),
в) лінійного (неоднорідного) першого порядку,
г) лінійного однорідного другого порядку зі сталими коефіцієнтами.
| 4.1.1. | а)  ,
б) ,
б) 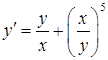 ,
в) ,
в)  ,
г) ,
г)  . .
| 4.1.2. | а) 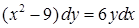 ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г)  . .
|
| 4.1.3. | а) 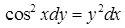 ,
б) ,
б) 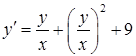 ,
в) ,
в)  ,
г) ,
г) 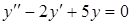 . .
| 4.1.4. | а)  ,
б) ,
б)  ,
в) ,
в) 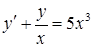 ,
г) ,
г) 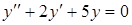 . .
|
| 4.1.5. | а)  ,
б) ,
б) 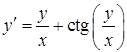 ,
в) ,
в) 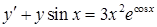 ,
г) ,
г)  . .
| 4.1.6. | а) 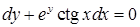 ,
б) ,
б) 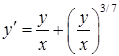 ,
в) ,
в)  ,
г) ,
г) 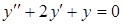 . .
|
| 4.1.7. | а)  ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г) 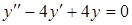 . .
| 4.1.8. | а)  ,
б) ,
б) 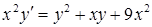 ,
в) ,
в)  ,
г) ,
г)  . .
|
| 4.1.9. | а) 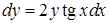 ,
б) ,
б)  ,
в) ,
в) 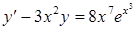 ,
г) ,
г)  . .
| 4.1.10. | а) 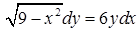 ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г)  . .
|
| 4.1.11. | а) 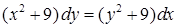 ,
б) ,
б)  ,
в) ,
в) 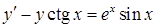 ,
г) ,
г)  . .
| 4.1.12. | а) 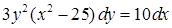 ,
б) ,
б) 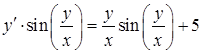 ,
в) ,
в)  ,
г) ,
г) 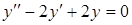 . .
|
| 4.1.13. | а)  ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г)  . .
| 4.1.14. | а) 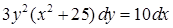 ,
б) ,
б) 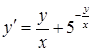 ,
в) ,
в) 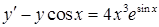 ,
г) ,
г)  . .
|
| 4.1.15. | а) 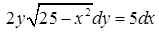 ,
б) ,
б) 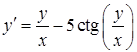 ,
в) ,
в)  ,
г) ,
г) 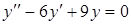 . .
| 4.1.16. | а)  ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г)  . .
|
| 4.1.17. | а)  ,
б) ,
б) 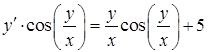 ,
в) ,
в)  ,
г) ,
г) 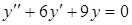 . .
| 4.1.18. | а)  ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г)  . .
|
| 4.1.19. | а)  ,
б) ,
б) 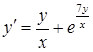 ,
в) ,
в)  ,
г) ,
г)  . .
| 4.1.20. | а)  ,
б) ,
б) 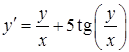 ,
в) ,
в) 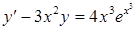 ,
г) ,
г) 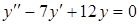 . .
|
| 4.1.21. | а)  ,
б) ,
б) 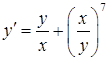 ,
в) ,
в) 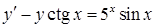 ,
г) ,
г) 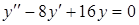 . .
| 4.1.22. | а)  ,
б) ,
б)  ,
в) ,
в) 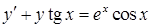 ,
г) ,
г) 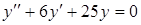 . .
|
| 4.1.23. | а) 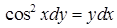 ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г)  . .
| 4.1.24. | а) 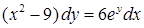 ,
б) ,
б) 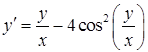 ,
в) ,
в) 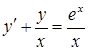 ,
г) ,
г) 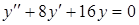 . .
|
| 4.1.25. | а) 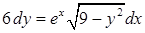 ,
б) ,
б) 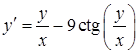 ,
в) ,
в)  ,
г) ,
г)  . .
| 4.1.26. | а) 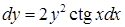 ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г)  . .
|
| 4.1.27. | а)  ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г) 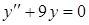 . .
| 4.1.28. | а) 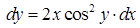 ,
б) ,
б)  ,
в) ,
в) 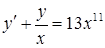 ,
г) ,
г)  . .
|
| 4.1.29. | а) 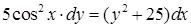 ,
б) ,
б)  ,
в) ,
в)  ,
г) ,
г) 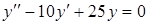 . .
| 4.1.30. | а)  ,
б) ,
б) 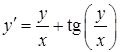 ,
в) ,
в)  ,
г) ,
г) 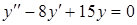 . .
|
5.1. Для фігури 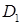 , що обмежена лініями, вказаними в завданні 3.3.х:
, що обмежена лініями, вказаними в завданні 3.3.х:
· записати подвійний інтеграл  (
(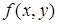 ‑ неперервна функція в
‑ неперервна функція в 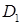 ) у вигляді повторного інтеграла та змінити порядок інтегрування,
) у вигляді повторного інтеграла та змінити порядок інтегрування,
· знайти масу пластини 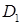 , якщо густина маси
, якщо густина маси 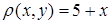 ,
,
· обчислити об’єм циліндричного тіла, обмеженого зверху площиною 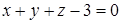 , знизу – площиною
, знизу – площиною 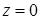 і з боків – прямою циліндричною поверхнею, що вирізає на площині
і з боків – прямою циліндричною поверхнею, що вирізає на площині 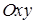 область
область 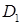 .
.
· знайти масу циліндричного тіла 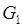 , якщо густина маси
, якщо густина маси 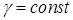 .
.
5.2. Обчислити криволінійний інтеграл:
| 5.2.1. |  вздовж дуги вздовж дуги  кола кола  від точки від точки 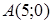 до точки до точки 
|
| 5.2.2. | 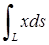 вздовж дуги вздовж дуги  параболи параболи  від точки від точки 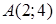 до точки до точки 
|
| 5.2.3. |  вздовж відрізка вздовж відрізка 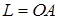 , де , де  , , 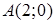
|
| 5.2.4. | 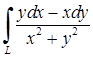 вздовж відрізка вздовж відрізка  , де , де 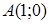 , , 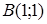
|
| 5.2.5. | 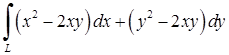 вздовж дуги вздовж дуги  параболи параболи 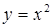 від точки від точки  до точки до точки 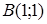
|
| 5.2.6. | 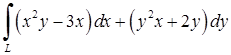 вздовж верхньої половини вздовж верхньої половини  еліпса еліпса 
|
| 5.2.7. | 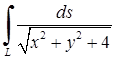 , де , де  – відрізок прямої, що з’єднуєточки О (0; 0) та А (2; 4) – відрізок прямої, що з’єднуєточки О (0; 0) та А (2; 4)
|
| 5.2.8. | 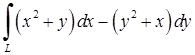 вздовж відрізка вздовж відрізка  , де , де 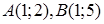
|
| 5.2.9. | 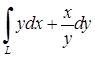 вздовж дуги вздовж дуги  кривої кривої 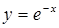 від точки від точки 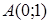 до точки до точки 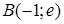
|
| 5.2.10. |  вздовж відрізка вздовж відрізка 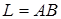 прямої від точки прямої від точки 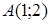 до точки до точки 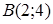
|
| 5.2.11. |  , де , де  – коло – коло  , , 
|
| 5.2.12. | 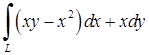 вздовж дуги вздовж дуги  параболи параболи 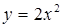 від точки від точки  до точки до точки 
|
| 5.2.13. |  вздовж дуги вздовж дуги  кривої кривої  від точки від точки 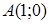 до точки до точки 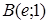
|
| 5.2.14. | 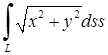 , де , де  – дуга кривої – дуга кривої 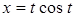 , ,  , ( , ( ) )
|
| 5.2.15. |  вздовж параболи вздовж параболи 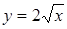 від точки від точки  до точки до точки 
|
| 5.2.16. | 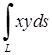 , де , де  – відрізок прямої, що з’єднуєточки О (0; 0) та С (0; 2) – відрізок прямої, що з’єднуєточки О (0; 0) та С (0; 2)
|
| 5.2.17. |  від точки від точки  до точки до точки 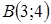 вздовж прямої, що проходить через ці точки вздовж прямої, що проходить через ці точки
|
| 5.2.18 | 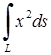 , де , де  – дуга кривої – дуга кривої  від точки з абсцисою від точки з абсцисою  до точки з абсцисою до точки з абсцисою 
|
| 5.2.19. | 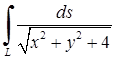 , де , де  – відрізок прямої – відрізок прямої 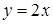 , що з’єднує точки з абсцисами 0 і 1 , що з’єднує точки з абсцисами 0 і 1
|
| 5.3.20. |  вздовж дуги параболи вздовж дуги параболи  від точки від точки 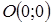 до точки до точки 
|
| 5.2.21. | 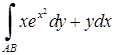 вздовж дуги параболи вздовж дуги параболи 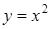 від точки від точки  до точки до точки 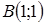
|
| 5.2.22 |  , де , де  – дуга кривої – дуга кривої  , ,  , , 
|
| 5.2.23 |  , де , де  – дуга параболи – дуга параболи 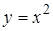 , що проходить від точки О (0; 0) до точки А (–1; 1). , що проходить від точки О (0; 0) до точки А (–1; 1).
|
| 5.2.24 | 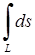 , де , де  – крива – крива  , , 
|
| 5.2.25 | 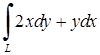 , де , де  - дуга параболи - дуга параболи  від точки від точки  до точки до точки 
|
| 5.2.26 | 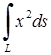 , де , де  – відрізок прямої – відрізок прямої  від точки з абсцисою від точки з абсцисою  до точки з абсцисою до точки з абсцисою 
|
| 5.2.27 |  вздовж лінії вздовж лінії 
|
| 5.2.28 |  , де , де  – лінія – лінія 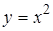 від точки з абсцисою від точки з абсцисою  до точки з абсцисою до точки з абсцисою 
|
| 5.2.29 | 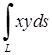 , де , де  – відрізок прямої, що з’єднуєточки О (0; 0) та – відрізок прямої, що з’єднуєточки О (0; 0) та 
|
| 5.2.30 |  , де , де  – коло – коло 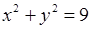
|
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 485; Нарушение авторских прав?; Мы поможем в написании вашей работы!