Полное исследование функций и построение графиков функций

Понятие производной, правила и формулы дифференциального исчисления широко применяются для исследования функций и построения графиков функций.

Схема исследования функций:

1. Найти область определения функции

2. Найти точки пересечения графика функции с осями координат

3. Выяснить особые свойства функции: четность, нечетность, периодичность

4. Найти интервалы монотонности функции

5. Найти экстремумы функции

6. Найти промежутки выпуклости, вогнутости графика с помощью второй производной

7. Найти точки перегиба

8. Дополнительные точка

9. На основании проведенного исследования построить график функции

Этот план исследования функции является примерным, можно менять порядок пунктов, некоторые совсем опускать, если они не подходят к данной функции. Пример: Исследовать функцию и построить ее график

Решение:

1. Область определения функции 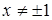. Следовательно график состоит из трех частей: на интервалах , , .

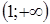2. Если 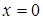, то . Значит график пересекает ось ОY в точке . Если то , 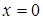. Значит график пересекает ось ОX в точке .

3. Функция 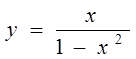является нечетной, т.к.

Следовательно, график симметричен относительно начала координат.

4. Найдем интервалы монотонности функции

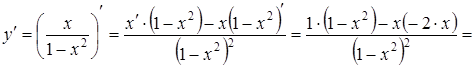
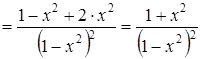
Заметим, что 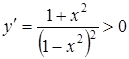при любых значениях х в области определения. Значит функция является возрастающей на каждом интервале области определения.

5. Т.к. уравнение 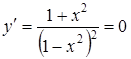не имеет решений , то функция не имеет экстремумов.

6. Исследуем функцию на выпуклость, вогнутость.

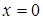точка перегиба.

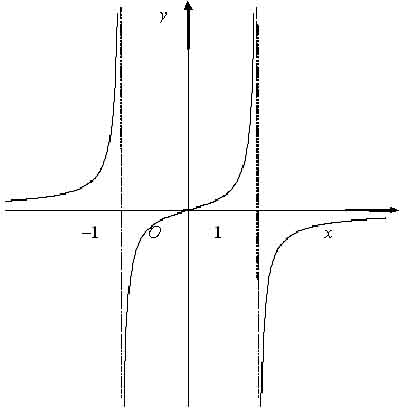
График изображен на рисунке

Дата добавления: 2014-12-17