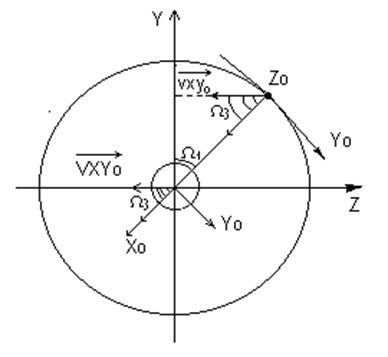
Формирование вектора скорости при отражении

Анализ условий вылета молекул из исследуемого объема

i-тое испытание заканчивается, когда молекула вылетает из исследуемого объема, то есть когда координата конечной точки прямолинейного участка траектории оказывается в области отверстия.

После расчета каждой конечной точки траектории при движении молекулы от стенки к стенке осуществляется проверка координаты y₂ моле-кулы. При этом также анализируется переменная Mx, которой присвоены различные значения в зависимости от вида поверхности, на которую попала молекула. При Mx=1, что соответствует переднему торцу, при y₂<0 и выполнении условия (26) молекула считается вылетевшей в отверстие на переднем торце; при Mx=-1, что соответствует заднему торцу, y2>0 и выполнении условия (26) молекула считается вылетевшей в отверстие на заднем торце.

После того, как i-тая молекула покидает исследуемый объем, начинается i+1ое испытание.

При столкновении молекулы, движущейся в исследуемом объеме, со стенкой происходит ее отражение. При этом меняется как модуль вектора скорости VV, так и направление ее движения, а следовательно и проекции скорости движения молекулы на оси X, Y, Z. Основные теоретические положения процесса отражения изложены в р.4.

Исходными данными для формирования вектора скорости служат координаты конечной точки прямолинейного участка траектории молекулы (в случае, если эта точка не находится в области отверстия), а также значение модуля вектора скорости до столкновения.

Модуль вектора отраженной скорости в соответствии с (12) определяется из выражения:

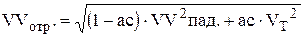(40)

где V_T - величина скорости, соответствующая температуре стенки, выбранная из распределения Максвелла.

После расчета модуля скорости, определяются его проекции на координатные оси XYZ. При этом проекции рассчитываются так, чтобы соблюдался диффузный закон отражения молекул от поверхности.

Для удобства моделирования распределения сформированной величины вектора скорости по проекциям вводится условная система координат X₀Y₀Z₀, ориентированная в пространстве таким образом, что плоскость Y₀Z₀ - касательная к поверхности в точке отражения, а ось X₀ направлена по нормали к этой поверхности. Началом координат в новой системе является точка отражения.

Проекции вектора скорости VV на оси координат X₀Y₀Z₀ определяются выражениями:

vx₀=VV×cosb;

vyz₀=VV×sinb;

vy₀=vyz₀×cosa; (41)

vz₀=vyz₀×sina,

где b - угол, который моделируется в соответствии с распределением вероятности P(b) по закону косинуса и задает отклонение вектора скорости от нормали к поверхности отражения в диапазоне [0,p/2];

a - угол между осью Y₀ и проекцией вектора отраженной скорости на плоскость Y₀Z₀, выбираемый при помощи генератора случайных чисел в диапазоне [0,2p].

Интенсивность рассеяния молекул в направлении b пропорциональна cosb, следовательно:

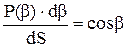, (42)

где db - телесный угол рассеяния;

dS - площадь рассеяния.

В свою очередь:

dS = 2p × r₀ × sinb × r₀ × db = 2p × r₀² × sinb × db, тогда:

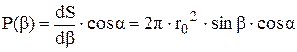
Полученную функцию отнормируем:

P(b) = m × P₀(b), где òP₀(b) = 1, тогда:

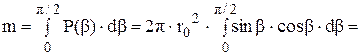p×r₀²

Таким образом, нормированная функция распределения P₀(b):

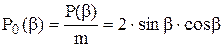(43)

В соответствии с выведенным соотношением угол b выбирается с использованием генератора случайных чисел по методу аналогичному методу, примененному при моделировании распределения Максвелла (см.п.7.2.1.).

После определения проекций вектора скорости в системе координат X₀Y₀Z₀ необходимо вернуться в исходную систему координат XYZ.

В случае отражения молекулы от торцов исследуемого объема эта процедура не представляет сложности, поскольку при отражении от переднего торца системы координат XYZ и X₀Y₀Z₀ совпадают, и, следовательно:

vx = vx₀, vy = vy₀, vz = vz_0. (44)

При отражении молекулы от заднего торца координатные оси Y и Y₀ совпадают, а Х и Х₀, Z и Z₀ взаимно противоположны, таким образом:

vx = - vx₀, vy = vy₀, vz = - vz_0. (45)

При отражении молекулы от боковой поверхности исследуемого объема и от анода для определения значения проекции вектора скорости на оси Y и Z, необходимо определить угол g между осью Y и проекцией вектора скорости отраженной молекулы на плоскость YZ. Для этого необходимо совместить начала координат систем XYZ и X₀Y₀Z₀, то есть перенести точку отражения в центр координат плоскости YZ (рис.1.7). При отражении молекулы от верхней части боковой стенки исследуемого объема (y₂>0) или нижней части анода (y₂<0) угол g составит:

g = W1 + p - W3.

Рис.1.7 Перенос координат относительно центра

При отражении молекулы от боковой стенки при y₂<0 или от анода

при y₂>0:

g = W₁ - W₃

Причем:

,

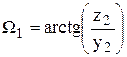Поскольку в случае отражения от поверхности анода или боковой стенки система координат X₀Y₀Z₀ ориентирована таким образом, что координатные оси Z₀ и X взаимно противоположны, а плоскости X₀Y₀ и YZ параллельны, то можно записать:

vx = -vz₀, 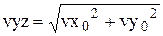(46)

Тогда проекции вектора скорости vy и vz при отражении от анода или боковой стенки определяются выражениями:

vy =vyz × cosg,

(47)

vz = vyz × sing

В случае, если отражение происходит в точке, одна из координат которой (y₂, z₂) равна нулю, то выражение для проекций вектора скорости на оси YZ принимают вид:

а) При отражении от анода:

- если y₂=0, то: 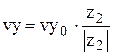, , 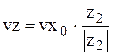(48)

- если z₂=0, то: , , (49)

б) При отражении от боковой стенки:

- если y₂=0, то: 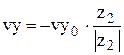, , (50)

- если z₂=0, то: , , 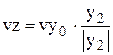(51)

Определение положения начала системы координат X₀Y₀Z₀ и, следовательно, выбор выражений для переноса проекций вектора скорости vx₀, vy₀, vz₀ на оси X, Y, Z происходит при анализе переменных Mx и My, значения которых определяются при расчете прямолинейного участка траектории движения молекулы и соответствуют той поверхности исследуемого объема, от которой отражается молекула.

Описанная процедура позволяет рассчитать значение вектора скорости молекулы при отражении ее от любой поверхности исследуемого объема с учетом изменения кинетической энергии при взаимодействии со стенкой, а так же задать ориентацию вектора скорости в пространстве таким образом, чтобы соблюдался закон диффузного отражения.

Дата добавления: 2014-11-29