Генерация вектора скорости молекулы и координат точки влета

Основные принципы моделирования вектора скорости молекул набегающего потока изложены в пункте 1.1.3. Проекции вектора направленной скорости постоянны и одинаковы для всех молекул набегающего потока и определяются по формуле (21).

Модуль температурной составляющей скорости VT представляет собой случайную величину, распределенную по закону Максвелла.

Максвелловское распределение задается следующим образом:

а) При помощи генератора случайных чисел задается значение вектора тепловой скорости V_T в диапазоне от 0 до 5 (скорость V_T нормирована относительно скорости молекулы, имеющей температуру стенок исследуемого объема).

б) В соответствии с законом Максвелла рассчитывается вероятность y того, что тепловая скорость молекулы будет иметь значение V_T:

y = V_T²×exp (1-V_T²).

в) При помощи генератора случайных чисел выбирается произвольное значение вероятности y₀ в диапазоне (0,1). Если y £ 0, то заданное значение вектора скорости V_T используется для дальнейших расчетов. Если y₀>y, процедура выбора V_T повторяется.

Таким образом, скорости V_T, вероятность появления которых в соответствии с распределением Максвелла мала (y<<1) будут встречаться в последовательности реже, чем скорости, для которых(y £ 1).

Проекции вектора температурной скорости V_T на оси X,Y,Z определяются следующим образом:

а) С помощью генератора случайных чисел определяется величина c в диапазоне (-1,1), которая является косинусом угла между направлением вектора те-пловой скорости и положительным направлением оси Х. Выражение:

vx_T = V_T×c (22)

определяет значение проекции вектора скорости на ось Х.

б) Проекция вектора температурной скорости на плоскость YZ определяется выражением:

vyz_T = V_T sin(arccos(c)).

Учитывая тригонометрическую формулу sin²c + cos²c= 1, получаем:

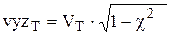(23)

В плоскости YZ направление вектора скорости равновероятно и определяется случайным углом e, который откладывается от положительного направ-ления оси Y. Угол e выбирается при помощи генератора случайных чисел в диапазоне (0,2p). Выражения для проекций вектора скорости на оси Y и Z имеют вид:

vy_T = vyz_T × cos(e),

vz_T = vyz_T × sin(e) (24)

Описанный метод задания проекций вектора тепловой скорости обеспечивает его равновероятное распределение в выбранной системе координат.

Итоговые проекции вектора скорости на координатные оси X, Y, Z

в соответствии с (9) представляют собой суммы соответствующих проекций векторов направленной и тепловой скоростей:

vx = vx_T + vx00,

vy = vy_T + vy00, (25)

vz = vz_T + vz00.

При каждом i-ом испытании необходимо задать точку влета молекулы в исследуемый объем, то есть координаты начала движения молекулы.

Как было описано выше, отверстия в исследуемом объеме, через которые осуществляется влет и вылет молекул, представляют собой полукольца с радиусами r₀₂ (внешний) и r₀₁ (внутренний), расположенные в нижней части переднего и в верхней части заднего торцов.

Торец, через который влетает i-ая молекула, определяет проекция вектора скорости vx. В случае vx>0 молекула влетает через отверстие в переднем торце (х₁ = 0), в случае vx<0 - через отверстие в заднем торце (х₁ = l). Для расчета V_xср0 - проекции на ось X средней скорости влета молекул в объем W, отнормированной по V_ст0, рассчитывается сумма проекций на ось X скоростей влета молекул в объем W: vn:= vn + abs (vx).

Координаты y₁, z₁ точек, в которых молекулы влетают в исследуемый объем, должны быть равномерно распределены по площади входных отверстий. Учитывая это, координаты точки влета i - ой молекулы в исследуемый объем выбираются следующим образом:

а) С помощью генератора случайных чисел определяется пара координат:

- координата z₁ в диапазоне от -1 до 1;

- координата y₁ в диапазоне от -1 до 0 для (х₁ = 0) или в диапазоне от 0 до 1 для (х₁ =l).

б) Анализируется выполнение условия нахождения выбранной пары координат внутри полукольца отверстия.:

r₀₂² > y₁² + z₁² > r₀₁². (26)

Это говорит о том, что выбранная пара находится внутри полукольца отверстия. Если условие (26) не выполняются, то генерируется новая пара чисел.

Таким образом, при большом количестве испытаний (n®¥) координаты точек влета молекул равномерно "засеивают" площади входных отверстий.

Расчет траектории движения молекулы включает в себя расчет времен пересечения молекулой границ расчетных объемов W_pk и определение координаты конечной точки прямолинейного участка траектории молекулы в исследуемом объеме W.

Для расчета требуемых времен и координат используются следующие начальные условия движения:

- начальная точка прямолинейной траектории движения молекулы с координатами x₁, y₁, z₁, которая может быть либо точкой влета молекулы в иссле-дуемый объем, либо конечной точкой предыдущей прямолинейной траектории движения молекулы (то есть точкой отражения);

- проекции вектора скорости молекулы, задаваемые либо при влете молекулы в исследуемый объем, либо при отражении молекулы от стенок объема.

Прямолинейная траектория движения молекулы описывается уравнением движения:

. (27)

Времена и координаты пересечения траектории с поверхностью рассчитываются путем решения системы из проекций на плоскость YZ и ось Х уравнения движения молекулы (27) и уравнения, описывающего пересекаемую поверхность.

Теперь рассмотрим процедуру поиска решения для случаев пересечения траектории движения молекулы с боковыми поверхностями цилиндров с радиусами rA, r₁, r₂, r₀. Для этого рассмотрим движение молекулы в плоскости YZ.

Проекцией боковой поверхности цилиндра на плоскость YZ является окружность, и следовательно, в общем случае система уравнений может быть записана следующим образом:

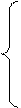
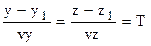
(28)

,

где r - радиус соответствующей окружности.

Решая систему (28), получаем:

(y₁+vyT)²+(z₁+vzT)²=r² (29)

Решив это уравнение относительно Т, получаем:

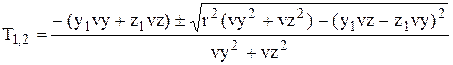(30)

или:

(31)

,

где t_max и t_min - времена пересечения молекулой боковой поверхности цилиндра радиуса r.

Если значения t_max и t_min - комплексные числа, то траектория движения молекулы не пересекает рассматриваемую поверхность; положительные значения t_max и t_min означают, что молекула движется извне по направлению к рассматриваемой поверхности; отрицательные значения t_max и t_min означают, что молекула находится вне рассматриваемого цилиндра и удаляется от него; если t_max >0, а

t_min <0, то начальная точка движения находится внутри рассматриваемого цилиндра.

Времена пересечения траектории движения молекулы с поверхностями торцов цилиндра определяются по проекции траектории движения молекулы на ось Х.

Координатами торцов по оси X являются: х = 0 (для переднего торца) и

х = l (для заднего торца), тогда времена пересечения траектории движения молекулы с торцами t₀и t₁ определяются выражениями:

. (32)

Для нахождения конечной точки прямолинейной траектории движения молекулы необходимо из времен t_max(r0), t_min(rA), t₀ и t₁ выбрать наименьшее положительное время -t_кон. И тогда:

x₂ = vx × t_кон + x₁

y₂ = vy × t_кон + y₁ (33)

z₂ = vz × t_кон + z₁.

По результатам выбора t_кон определяется поверхность, на которую попадает молекула. При этом задаются значения переменных Mх и My, определяющих эту поверхность: если молекула попадает на передний торец (t_кон = t₀), то Mх = 1, если на задний (t_кон = t₁), то Mх = -1; для боковой поверхности и анода - Mх = 2, причем при попадании молекулы на боковую стенку исследуемого объема (t_кон =t_max(r0)) - My = 1, а при попадании молекулы на анод (t_кон = t_min(rA)) - My = -1.

Для определения начального и конечного времени нахождения молекулы в расчетном объеме, ограниченном радиусами r₁ и r₂ и длиной l, необходимо рассчитать вещественные времена t_max(r2), t_min(r2), t_max(r1) и t_min(r1) и время t_кон.

Значение T_min- начального времени нахождения молекулы в расчетном объеме определяется местоположением начальной точки, знаком величин t_max(r1,r2), t_min(r1,r2), а также условием не превышения значениями t_max(r1,r2) или t_min(r1,r2) времени t_кон. Так:

- если r₁²<y₁²+z₁²<r₂², то T_min=0;

- если y₁²+ z₁²>r₂² и 0< t_min(r2)< t_кон, то T_min=t_min(r2);

- если t_min(rА) <0 или мнимое, 0<t_max(r1) <t_кон, то T_min=t_max(r1).

Значение T_max - конечного времени нахождения молекулы в расчетном объеме - определяется из значений t_кон, t_min(r1)< t_кон, t_max(r2)< t_кон. Так:

- если значение t_min(rA)- мнимое, а t_max(r1,r2) - реальное и 0<t_min(r1)< t_max(r1)< t_кон, то траектория молекулы пересекает расчетный объем дважды; в этом случае выби-раются две пары значений T_min, T_max;

- если t_min(r2) мнимое или >t_кон,то это означает, что молекула не попадает в расчетным объем на данном прямолинейном участке траектории.

Результатом описанной процедуры является одна или две пары значений времен влета T_min и вылета T_max для расчетного объема - в случае, если молекула в него попадает на данном прямолинейном участке траектории, а также координаты конечной точки прямолинейного участка движения x₂, y₂, z₂ и значения

параметров Mx и My, определяющие поверхность, на которую попадает молекула.

1.1.10. Расчет времен пребывания молекулы в частных объемах W_pk

Расчет времен пребывания молекулы в частном объеме необходим для расчета относительного распределения концентраций молекул внутри цилиндра. Как показано в разделе 2, расчетный объем поделен на 2 × ks × ps частных объемов W_pk, времена нахождения молекулы в которых, есть разность времен влета и вылета.

Координаты влета и вылета молекул из частного объема и соответствующие им времена рассчитываются путем решения системы из проекций на плоскость YZ и ось Х уравнения движения молекулы (27) и уравнений поверхностей, образующих частный объем. Времена влета и вылета из частного объема должны быть в пределах начального и конечного времени нахождения молекулы в расчетном объеме.

Рассмотрим процедуру нахождения координат и времен пересечения траектории с образующими частный объем W_pk плоскостями. В проекции на плоскость YZ частный объем представляется в виде кольцевого сектора, внешняя и внутренняя дуги которого - части окружностей, соответствующие границам расчетного объема. Координаты пересечения траектории движения молекулы с радиальными границами кольцевого сектора рассчитываются из системы уравнений движения и образующей сектора, описываемой выражением:

y×sinl - z×cosl = 0, (34)

где l - угол между осью Y и радиальной границей сектора.

В общем виде система уравнений может быть записана следующим обра-зом:

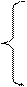y × vz – z × vy = vz × y₁ – vy × z₁

(35)

y × sin l - z × cos l = 0

Решением системы уравнений являются координаты:

(36)

,

при условии, что:

,

т.к. рассматриваем только положительную часть радиальной границы сектора.

Время пересечения траекторией боковой поверхности частного объема рассчитывается из выражения:

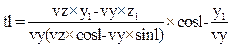. (37)

Так как расчетный объем поделен в плоскости YZ на четное число секторов, то будем для секторов k_R Î [1,ks] (правая половина проекции) отсчитывать углы a от 0 до p, а для секторов kL Î [ks+1,2ks] (левая половина) - углы l Î [0,-p] с интервалом p/ks. Тогда из выражения (37) получаем:

,

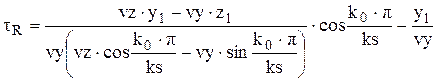(38)

,

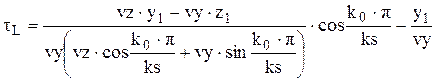где k₀ Î [0,ks].

Зная значения t_R и t_L можно рассчитать времена пересечения траектории движения молекулы со всеми радиальными границами секторов. Времена пересечения траектории движения с плоскостями, разделяющими расчетный объем на ps равных долей по оси Х, рассчитываются из выражений:

, (39)

где х - координата плоскостей, являющихся границами долей, на которые разбит расчетный объем вдоль оси Х.

Координата х принимает значения: (p0 × l)/ps; p₀ Î[0,ps].

Определение значений времен нахождения молекулы в частном объеме производится следующим образом:

а) Задается пара значений p₀ и p₀+1. Для них рассчитываются времена

t_0¸1 и t_0¸1+1. Далее:

- если хотя бы одно из них больше T_min и меньше T_max, или одно из них больше T_max, а другое меньше T_mшт, то из времен t_0¸1, t_0¸1+1,T_min, T_max выбираются времена влета t0 и вылета t00 из долевого объема - объема, ограниченного поверхностями цилиндров с r1, r2 и плоскостями х'=(p₀×l)/ps и х"=((p₀+1) × l)/ps;

а) если оба значения t_0¸1 и t_0¸1+1 меньше T_min или больше T_max, то берется следующая пара значений p₀ и p₀₊₁, и расчет повторяется.

б) Для пары значений k₀ и k₀₊₁ рассчитываются времена t_R и t_R+1, t_L и t_L+1 - как времена пересечения радиальных границ секторов k_R и k_L=2 × ks+1-k_R. Из времен t0 и t00 и времен t_R, t_R+1 , t_L и t_L+1 выбираются времена влета и вылета для частных объемов в случае, когда хотя бы одно из времен t_R, t_R+1, t_L и t_L+1 лежит в пределах от t0 до t00, или же времена t0 и t00 лежат в пределах от t_L,R до t_L+1,_R+1. Время нахождения молекулы в объеме Wpk, как разница времен влета и вылета, прибавляется к содержимому ячейки nk[k,p] и записывается в ячейку nk[k,p] матрицы времен. Расчет происходит в цикле от k₀=0 до k₀=ks-1 - когда будут рассчитаны времена t_L,R ¸ t_L+1,R+1 для секторов k_R=ks и k_L=ks+1.

в) Задается следующая пара значений p₀и p₀₊₁, вплоть до значений p₀=ps-1 и p0=ps.

Описанный механизм расчета и выбора повторяется для каждого прямолинейного участка траектории молекулы, и, суммируя времена для большого количества испытаний, получаем необходимые статистические данные для расчета распределения концентраций молекул в расчетном объеме.

Дата добавления: 2014-11-29