Моделирование движения молекулы внутри объема

Движение молекулы внутри датчика рассматриваем как совокупность прямолинейных траекторий, первая из которых начинается с точки влета молекулы в объем, а последняя завершается вылетом молекулы из объема W. При этом, началом прямолинейной траектории может быть как точка влета молекулы в объем, так и конечная точка предыдущей прямолинейной траектории (точка отражения молекулы от внутренней поверхности), а концом - либо точка попадания молекулы на внутреннюю поверхность объема, либо точка вылета из объема.

Таким образом моделирование движения молекулы внутри объема включает:

- расчет траектории движения молекулы;

- анализ условий вылета молекулы;

- формирование вектора скорости при отражении.

Исходными данными для расчета траектории движения молекулы являются координаты начала движения и проекции вектора скорости молекулы на оси координат X,Y,Z. Целью расчета является определение координат точки пересечения молекулой внутренней поверхности объема.

Анализ условий вылета молекулы заключается в сравнении координат точки пересечения молекулой внутренней поверхности объема с координатами зон прозрачности и непрозрачности и принятии решения либо о вылете молекулы из объема, либо об ее отражении от внутренней поверхности объема.

Для определения вектора скорости молекулы, отраженной от внутренней поверхности объема, необходимо смоделировать механизм ее взаимодействия с внутренней поверхностью.

В общем случае можно ожидать следующие виды взаимодействий молекулы с поверхностью: адсорбция на поверхности, ионизация молекулы при отражении, отражение нейтральной молекулы. Ограничимся моделированием отражения нейтральной молекулы от шероховатой (в микромасштабе) поверхности, считая первые два вида взаимодействия в моделируемых условиях маловероятными. В результате моделирования должны быть определены модуль вектора скорости отраженной молекулы и его проекции на оси координат.

При отражении молекулы от твердой поверхности происходит обмен энергией между молекулой и поверхностью. При этом, доля энергии, передаваемая молекулой или приобретаемая ею при столкновении с поверхностью, определяется характером взаимодействия и свойствами поверхности.

Величиной, характеризующей тип взаимодействия и свойства поверхности (механические и химические) твердого тела, является коэффициент аккомодации энергии молекулы, определяемый выражением [1,с.215]:

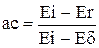, (11)

где Ei - энергия падающей молекулы;

Er - энергия отраженной молекулы;

Ed - энергия, соответствующая температуре поверхности T.

Так как

,

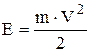то для модулей скоростей можно записать:

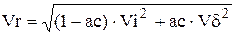, (12)

где Vr - модуль скорости отраженных молекул;

Vi- модуль скорости падающих молекул;

Vd - модуль скорости молекул, имеющих температуру равную температуре поверхности.

Выражение (12) справедливо для статистически усредненных значений модулей скоростей, что и должно быть обеспечено для совокупности моделируемых отражений.

Величина коэффициента аккомодации ac для условий, сходных с условиями, при которых проводится моделирование, составляет от 0.5 до 1 [2, с.95].

Значения проекций вектора скорости отраженной молекулы определяются принятым для моделирования законом рассеяния молекулы от внутренней поверхности объема. Крайними случаями рассеяния являются зеркальное отражение и диффузное рассеяние, подобное отражению света от шероховатой белой поверхности [2, с.85].

В общем случае, сумму этих видов отражений описывает зеркально-диффузная функция распределения [3, п.1.7], [1, п.5.4]. Однако, из результатов экспериментов, представленных в [2, с.89] следует, что для полированных металлических поверхностей при всех углах падения довольно точно соблюдается рассеяние по диффузному закону, не учитывающему зеркальную составляющую отражения. При этом отраженные молекулы рассеиваются в пределе полусферы таким образом, что интенсивность потока отраженных молекул в телесном угле dw пропорциональна косинусу b между нормалью к поверхности, от которой происходит отражение (ось X0) и направлением рассеяния и не зависит от угла падения (рис.1.5).

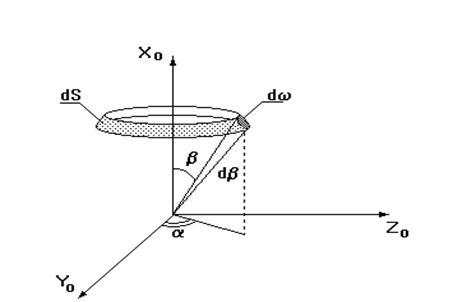
Рис.1.5 Интенсивность потока отраженных молекул в телесном угле dw

Закон диффузного рассеяния (или закон косинуса), как функция распределения интенсивности потока отраженных молекул, был принят при моделировании отражения молекул от внутренних поверхностей объема.

Дата добавления: 2014-11-29