Биомеханика мышцы

Мышцы можно представить как сплошную среду, то есть среду, состоящую из большого числа элементов, взаимодействующих между собой без соударений и находящихся в поле внешних сил. Мышца одновременно обладает свойством упругости и вязкости, то есть является вязко-упругой средой. Для такой среды предполагаются справедливыми законы классической механики.

Фундаментальными понятиями механики сплошных сред являются деформация, напряжение, упругость, вязкость, а также энергия и температура.

а). Упругость - свойство тел менять размеры и форму под действием сил и самопроизвольно восстанавливать их при прекращении внешних

Рис. 7.4. Зависимость максимального значения силы Р, развиваемой

при изометрическом сокращении, от начальной длины саркомера I (а) и степени перекрытия актиновых и миозиновых нитей (б) воздействий. Упругость тел обусловлена силами взаимодействия его атомов и молекул. При снятии внешнего воздействия тело самопроизвольно возвращается в исходное состояние,

б). Вязкость - внутреннее трение среды.

в). Вязкоупругость — это свойство материалов твердых тел сочетать упругость и вязкость.

г). Деформация - относительное изменение длин: .

где l - начальная длина, ∆l - значение удлинения, может менять знак.

д). Напряжение механическое σ - мера внутренних сил, возникающих при деформации материала. Для однородного стержня: .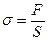

где S — площадь сечения, F — сила, приложенная к стержню.

Упругая деформация возникает и исчезает одновременно с нагрузкой и не сопровождается рассеянием энергии. Для упругой деформации справедлив закон Гука: ,

где Е - модуль Юнга, определяемый природой вещества.

Пассивные механические свойства вязкоупругой среды можно моделировать сочетанием упругих и вязких элементов.

Мышца не является ни чисто упругим, ни чисто вязким элементом. Мышца - вязкоупругий элемент.

Активное сокращение мышцы. Для исследования характеристик сокращающихся мышц используют два искусственных режима:

1. Изометрический режим, при котором длина мышцы l = const, а регистрируется развиваемая сила F(t).

2. Изотонический режим, при котором мышца поднимает постоянный груз Р = const, а регистрируется изменение ее длины во времени ∆l (t).

Максимальная сила Р₀, которую может развивать мышца, зависит от ее начальной длины и области перекрытия актиновых и миозиновых нитей, в которой могут замыкаться мостики: при начальной длине саркомера 2,2 мкм в сокращении участвуют все мостики.

Поэтому максимальная сила генерируется тогда, когда мышца предварительно растянута на установке так, чтобы длины ее саркомеров были близки к 2,2 мкм.

При изотоническом режиме к незакрепленному концу мышцы подвешивают груз Р. После этого подается стимул и регистрируется изменение длины мышцы во времени: ∆l(t). Чем больше груз Р, тем меньше укорочение мышцы и короче время удержания груза. При некоторой нагрузке Р = Р₀ мышца совсем перестает поднимать груз; это значение Р₀ и будет максимальной силой изометрического сокращения для данной мышцы.

Дата добавления: 2014-11-29