Потенциал

Из законов, описывающих электростатическое поле, вытекают некоторые из его свойств. Электростатическое поле является центральным, то есть оно имеет источник (центр) и свойства его одинаковы во всех направлениях. Это подтверждается, в частности, теоремой Гаусса. Силовые линии поля не пересекаются и в этом плане электростатическое поле похоже на гравитационное.

Вектор напряжённости является силовой характеристикой электрического поля. С энергетической точки зрения электрическое поле характеризуется потенциалом в каждой точке (или разностью потенциалов двух точек).

Электрическая энергия – это самый универсальный вид энергии, который может быть превращён в любой другой вид. Поэтому изучение энергетической характеристики электрического поля приобретает особое значение.

Потенциал и вектор напряжённости в каждой точке поля связаны между собой, поэтому по изменению потенциала в каждой точке можно судить о силовых характеристиках электрического поля, то есть рассчитывать электрическое поле.

3 Циркуляция вектора напряжённости

Заряд, помещённый в электростатическое поле, перемещается под действием кулоновских сил. Действие этих сил в каждой точке характеризуется величиной вектора напряжённости .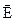

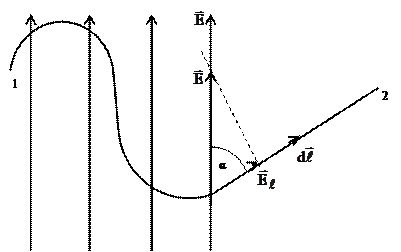Так как при взаимодействии зарядов происходит превращение одной формы движения материи в другую (электрической в механическую), то естественно этот процесс следует характеризовать величиной работы силы Кулона. При перемещении заряда 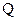из точки поля I в точку 2 совершается работа, которую можно вычислить следующим образом.

Рисунок 15

Разобьём путь 1-2 (рисунок 15) на элементы :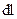

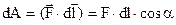
Тогда полная работа на пути 1-2 будет равна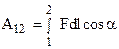

Заменяя 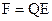, получим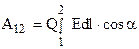 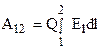. (10)

Таким образом, работа перемещения заряда зависит от характера поля и величины движущегося заряда 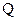, перемещения/ Как видно из выражения (10), отношение работы перемещения заряда из одной точки поля в другую к величине этого заряда

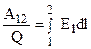
определяется лишь характером поля и положением точек 1 и 2.

Эта величина называется разностью потенциалов двух точек и обозначается так:

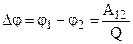. (11)

В качестве примера рассмотрим поле точечного заряда (рисунок 16). Так как в этом случае

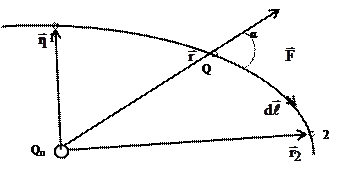
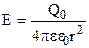, то из формулы (10) получим .

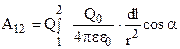Рисунок 16

Учитывая, что 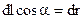, получим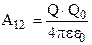 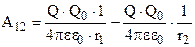. (11)

Анализ полученного выражения позволяет сделать два очень важных заключения:

1) известно, что работа может быть вычислена как изменение энергии системы. Следовательно, каждое из слагаемых в формуле (12) представляет собой выражение энергии взаимодействия точечных зарядов 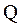и 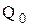в различных точках:

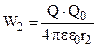, . (12)

Так как величина энергии в этом случае зависит лишь от взаимного расположения зарядов 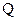и 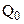и от типа взаимодействия (от характера сил), то это потенциальная энергия.

2) Из выражения (12) видно, что работа перемещения заряда в электростатическом поле не зависит от пути перемещения и, следовательно, работа по замкнутому контуру равна нулю. Это справедливо не только для полей точечных зарядов, но и для электростатических полей зарядов любой формы. Выражение (10) в этом случае имеет вид

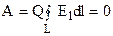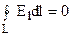, . (13)

Интеграл называется циркуляцией вектора 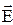по замкнутому контуру .

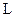Итак, циркуляция вектора напряжённости электростатического поля по произвольному замкнутому контуру равна нулю. Это значит, что электростатическое поле является потенциальным.

Помимо разности потенциалов, характеризующие две точки поля, используют понятие потенциала, который является энергетической характеристикой каждой точки поля. Введём это понятие, исходя из выражения (12) для поля точечного заряда:

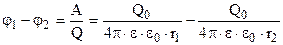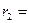
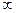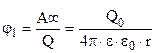,при , .(14)

В силу произвольности выбора точки I индекс можно опустить.

Потенциалом поля в данной точке называется скалярная величина численно равная работе перемещения единичного заряда из заданной точки поля в бесконечность:

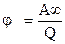. (15)

С другой стороны, при 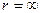из (11) получим ,

где W – потенциальная энергия системы зарядов 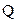и 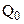. В связи с этим можно дать другое, равноценное первому, определение потенциала.

Потенциал есть физическая величина, численно равная потенциальной энергии единичного заряда, помещённого в данную точку поля

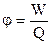(16)

На практике с бесконечностью дела не имеют, а определяют потенциал относительно другой точки, относительно Земли или заземлённого (зануленного) корпуса прибора. Точно так же потенциал (потенциальную энергию) поля тяготения часто определяют относительно поверхности Земли.

Принцип суперпозиции выполняется и для потенциала, поэтому потенциал поля системы зарядов равен сумме потенциалов полей каждого заряда в отдельности:

.

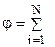
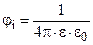
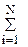
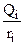Из выражений (15) и (16) устанавливается единица измерения потенциала – вольт: I B = I Дж/ I Кл.

5 Cвязь между напряжённостью и разностью потенциалов

Электростатическое поле можно задать значениями либо вектора напряжённости 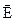, либо потенциала 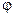в каждой точке. Очевидно, что между этими величинами существует связь.

Элементарная работа перемещения заряда в электростатическом поле может быть вычислена так: 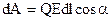или 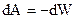, 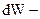убыль потенциальной энергии.

Приравнивая правые части обоих равенств, получим 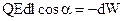, так как 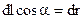, то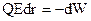

Поделим последнее выражение на 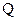. Так как 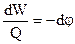, то 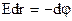, тогда

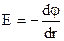(17)

В соответствии с выражением (18) величина напряжённости электрического поля зависит от скорости изменения потенциала вдоль радиус – вектора. Если заряд, создающий поле. является точечным, то скорость изменения потенциала вдоль радиус – вектора является максимальной по величине. В математике для характеристики максимальной скорости изменения какой – либо скалярной величины по направлению вводят понятие градиента (grad) Градиентом какой – либо величины называется вектор, модуль которого равен максимальной скорости изменения этой величины, направленный в сторону наиболее быстрого её возрастания. С учётом этого равенство (17) можно записать и в векторном виде: 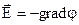(18)

Знак «–» в записи (18) отражает то обстоятельство, что вектор напряжённости направлен в сторону наиболее быстрого убывания потенциала. Для однородного электростатического поля 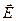= сonst, т. е. ,

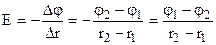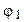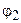где и - потенциалы точек, удалённых от начала отсчёта на расстояния r₁ и r₂ . В электротехнике разность потенциалов 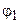- 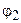называют напряжением между двумя точками.: 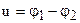.Т. о. для однородного поля .

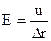Графически электрическое поле можно изобразить с помощью эквипотенциальных поверхностей, то есть поверхностей равного потенциала 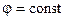. Для этих поверхностей 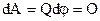, а так как 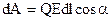, то , то есть вектора напряжённости перпендикулярны эквивалентным поверхностям (рисунки 17 и 18).

Рисунок 17 Рисунок 18

Из формул (12) и (13) следует, что убыль потенциальной энергии единичного положительного заряда при переходе из одной точки поля в другую численно равна работе сил поля по перемещению заряда между этими точками: .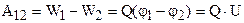

При перемещении заряда происходит преобразование электрической энергии в механическую.

Так как электрическое поле является потенциальным. а электрические силы – консервативными, то при таком преобразовании выполняется закон сохранения энергии.

Дата добавления: 2014-11-29