Неоднородные цепи

Электрическая цепь, в которой непрерывное протекание тока обеспечивается за счет сторонних сил, называется неоднородной. На неоднородном участке цепи действуют как электростатические (кулоновские), так и сторонние силы и закон Ома в дифференциальной форме в этом случае записывается как

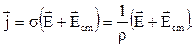. (21)

Рисунок 44

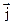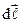Выведем закон Ома для неоднородного участка цепи в интегральной форме. Рассмотрим тонкий проводник, в котором и параллельны (рисунок44).

Умножим (21) на 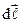скалярно и проинтегрируем его от точки 1 до точки 2 . (22)

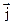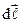Так как векторы и параллельны, то левую часть этого равенства можно представить в виде , (23)

где S – поперечное сечение проводника, (R+r) – полное сопротивление участка 1-2 (с учетом внутреннего сопротивления источника сторонних сил r).

Правая часть равенства (22) представляет собой работу кулоновских и сторонних сил и с учетом равенств (20), (23) выражение (21) можно записать

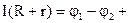e. (24)

Эта формула выражает закон Ома для неоднородного участка цепи в интегральной форме. Если концы цепи 1 и 2 (рисунок 5) соединить, получим замкнутую цепь, в которой 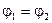. Из (24) следует . (25)

Формула (25) выражает закон Ома для замкнутой цепи. Если цепь разомкнута, то I = 0. Тогда из (24) следует, что e 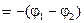, то есть напряжение на клеммах источника при разомкнутой цепи равно его ЭДС со знаком «минус». При 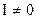падение напряжения на потребителе (IR) меньше ЭДС IR = e - Ir.

Максимальный ток, который может обеспечить источник ЭДС, определяется условием R = 0 (режим «короткого замыкания»). При этом .

Если цепь неизвестна, то по соединению в ней элементов закон Ома позволяет анализировать режим их работы.

Каждый источник тока характеризуется КПД () и мощностью (Р), которые зависят от характеристик источника тока и потребителя .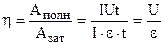

Из зависимости P(R) следует, что при некотором значении сопротивления нагрузки R, мощность на потребителе максимальна. Для нахождения R_max достаточно исследовать функцию на экстремум 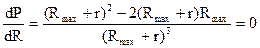. Отсюда следует, что , то есть при R = r мощность, выделившаяся на потребителе, достигает максимального значения.

Дата добавления: 2014-11-29