Законы Ома и Джоуля-Ленца в дифференциальной форме

Выведем закон Ома для металлов, исходя из модели электронного газа.

Рассчитаем плотность тока .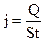

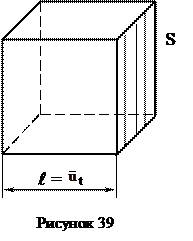Для подсчета заряда, переносимого через площадку S, выберем параллелепипед с основанием S = 1 м² (рисунок 2). Число электронов, заключенных в объеме V параллелепипеда длиной 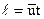, будет равно числу N электронов, пересекающих площадку S = 1м² в 1 с: 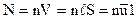(S = 1),

Тогда

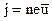. (4)

где n – число электронов в единице объема – концентрация электронов.

Найдем среднюю скорость дрейфа , применяя к электрону II закон Ньютона

, ,

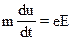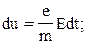
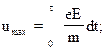
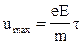где t - время свободного пробега, которое можно найти по формуле , так как .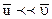

Таким образом, 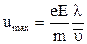, а среднее значение, , (5)

где 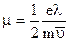, характеризует скорость при Е = 1 В/м и называется подвижностью.

Подставляя (5) в (4), получим

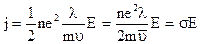, (6)

где 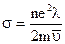называется удельной электропроводностью металла. Обратная ей величина называется удельным сопротивлением.

Выражение (6), утверждающее прямую пропорциональную зависимость между плотностью тока и напряженностью поля, называется законом Ома в дифференциальной (локальной форме). С учетом направлений векторов 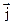и 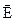соотношение (6) можно записать и в векторном виде .

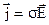Электронная теория проводимости позволяет понять механизм выделения тепла при прохождении по проводнику электрического тока. Электрическое поле совершает работу и ускоряет электроны в металлах. Накапливаемая ими энергия при столкновениях с ионами передается решетке и нагревает металл. Отсюда можно теоретически вывести закон Джоуля-Ленца.

Будем считать, что в начале свободного пробега, сразу после соударения, cкорость направленного движения электрона u = 0. К концу свободного пробега его скорость становится равной u_max. Электрон приобретает кинетическую энергию

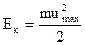. (7)

Так как 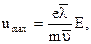то равенство (7) имеет вид 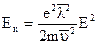. (8)

Столкнувшись с ионом, электрон, по предположению, полностью передает приобретенную кинетическую энергию кристаллической решетке. Сообщенная решетке энергия идет на увеличение внутренней энергии металла, то есть на его нагревание.

Каждый электрон испытывает за 1 секунду z соударений 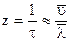; сообщая всякий раз решетке энергию (8).

Следовательно, в единице объема за единицу времени должна выделяться теплота 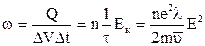, (9)

где n – концентрация свободных электронов.

Множитель при Е² есть не что иное, как удельная проводимость .

С учетом последнего, (9) можно переписать так . (10)

Полученное соотношение (10) представляет собой математическое выражение закона Джоуля-Ленца в дифференциальной форме: количество теплоты, выделившееся в единице объема проводника при протекании тока в единицу времени (тепловая мощность), пропорционально квадрату напряженности поля.

Используя закон Ома (6), находим .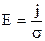

Тогда (10) приобретает вид 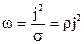. (11)

С другой стороны, запись закона Джоуля-Ленца (10) можно представить в виде 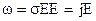. (12)

Формулы (10) - (12) эквивалентны.

Дата добавления: 2014-11-29