Теорема Максвелла

Представим себе замкнутую поверхность s, внутри которой как-либо распределены электрические заряды q ₁ ,q ₂, q ₃ и т. д. Пусть ds представляет собою элемент этой поверхности (рис. 106).

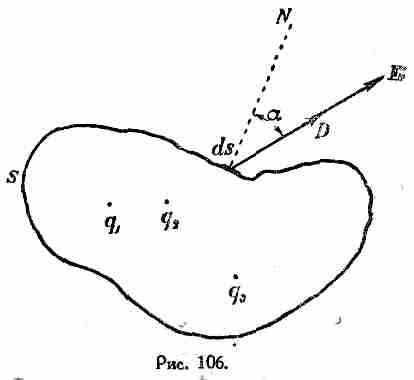
Обозна­чим через a угол, образуемый внешнею нормалью N к этому эле­менту поверхности и направлением электрической силы (напряжения поля) E в той точке, где находится рассматриваемый элемент по­верхности.

Если диэлектрическая постоянная среды есть e и если при этом e постоянно для всех точек среды, то по теореме Гаусса, выве-

денной в § 2 для магнитного поля и формально распространяемой также на электрическое поле, имеем:

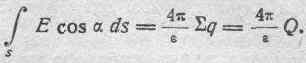
Разделив обе части этого равенства на 4p/e и внеся постоянный множитель e/4pпод знак интеграла, получим:

Выражение eE/4pдолжно

иметь размерность коли­чества электричества на единицу поверхности. Максвелл положил

D= e E/4p, (30)

на основании чего полу­чается крайне простая по форма и весьма важная по содержанию зависимость:

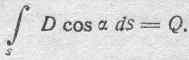
В этом выражении величина Dcosads есть поток электриче­ского смещения сквозь элемент поверхности ds, a D cosa — нор­мальная составляющая электрического смещения сквозь этот эле­мент поверхности.

Для неоднородных и анизотропных диэлектриков, у которых e не постоянно, мы не умеем доказать аналитически справедливость соотношения (31), но Максвелл ввел гипотезу, согласно которой оно справедливо для любых диэлектриков, независимо от их физи­ческих свойств. Все следствия, которые были выводимы из этого допущения, оправдывались при опытной проверке, и, таким образом, они в полной мере подтверждают справедливость высказанной Максвеллом гипотезы. До сих пор неизвестно ни одного факта, находящегося с ней в каком-либо противоречии.

Таким образом, мы будем считать справедливым в самом общем случае соотношение (31):

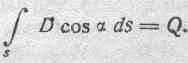
Понимая его в этом обобщенном смысле, мы будем называть его теоремой Максвелла. Итак, теорема Максвелла гласит: полное

электрическое смещение сквозь любую замкнутую поверхность в направлении изнутри наружу равно полному количеству электри­чества, находящегося внутри этой замкнутой поверхности.

Дата добавления: 2014-11-29