Электроемкость и диэлектрическая постоянная

Допустим, что потенциал какого-либо проводящего тела есть U, а потенциалы всех других проводников, находящихся в электриче­ском поле, равны нулю. В этом случае между потенциалом данного тела U и его зарядом q существует прямая пропорциональность, что выражается соотношением:

q = CU. (60)

Коэффициент пропорциональности С называется электроемко­стью или просто емкостью проводника. Как это явствует из при­веденного основного соотношения (60), электроемкость проводника численно измеряется величиной заряда на этом проводнике, когда его потенциал равен единице, а потенциалы всех остальных про­водников; находящихся в электрическом поле, равны нулю.

Вообще говоря, емкость проводника зависит, во-первых; от геометрических условий, т. е. от размеров данного проводящего тела и других проводников в рассматриваемой системе, а также от расстояний между ними. Во-вторых, при прочих равных условиях емкость зависит от свойств среды, заполняющей пространство, где создано электрическое поле, т. е. от свойств диэлектрика.

Рассмотрим сначала случаи, когда в качестве диэлектрика мы имеем пустоту.

Мы будем иметь простейший случай емкости, если предположим, что данный проводник расположен беспредельно далеко от всех других тел. При этом емкость проводника будет определяться только его геометрическими размерами. В случае уединенного шара

(рис.127), заряд которого равен q, а радиус есть r, емкость можно легко рассчитать следующим образом.

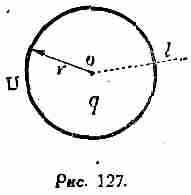
Потенциал шара выразится согласно определению (см. § 58) так:

где l есть радиальная линия, вдоль которой берется интеграл элек­трической силы от поверхности шара до бесконечности и начало которой совпадает с центром шара. Пользуясь теоремой Гаусса, не трудно показать, что электрическая сила в некоторой точке, взятой вне равномерно наэлектризованного шара, будет такова, как если бы все электричество, распределенное на шаре, было сосредоточено в его центре. Таким образом, в точке, удаленной на расстояние l от центра рассматриваемого шара, будем иметь:

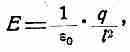
и потенциал шара может быть представлен в следующем виде:

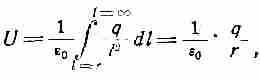
откуда получаем для уединенного шара:

q =e₀ rU.

Таким образом, электроемкость шара, уединенно расположенного в пустоте, выражается так:

C=e₀ r. (61)

На основании этого соотношения за единицу емкости в абсо­лютной электростатической системе единиц принимается емкость уединенного в пустоте шара, радиус которою равен одному сантиметру.

На практике (в особенности в радиотехнике) емкости весьма часто измеряют в подобных электростатических единицах, называя их просто сантиметрами в силу соотношения (61), в котором e₀=1. Но, кроме того, в тех случаях, когда приходится иметь дело с большими емкостями, например, в так называемой технике сильных токов, пользуются практической электромагнитной единицей емкости, называемой фарадой и согласованной с другими практическими электромагнитными единицами. Связь между названными двумя единицами емкости такова:

1 фарада=9•10¹¹ абс. эл.-стат. единиц,

1 микрофарада=9•10⁵ абс. эл.-стат. единиц.

Два проводника, изолированные один от другого и помещенные вблизи друг друга, образуют так называемый конденсатор. При этом, даже при сравнительно малой разности потенциалов между проводниками, заряд на каждом из них может быть значителен. Эти два проводника могут быть расположены таким образом, что их заряды получаются равными по величине и противоположными по знаку. В таком случае емкость конденсатора численно изме­ряется величиною заряда на том или другом проводнике, когда разность потенциалов между этими проводниками равна единице. Соотношение, связывающее заряд конденсатора с разностью потен­циалов на его проводниках или обкладках, совершенно подобно основному соотношению (60):

q = C (U ₁- U ₂). (62)

Здесь коэффициент С и есть емкость конденсатора. Приведенное определение емкости конденсатора вполне согла­суется с данным в начале этого параграфа определением емкости проводника и в точности совпадает с ним, если потенциал одного из проводников, образующих конденсатор, примем равным нулю.

Пользуясь представлением о фарадеевских трубках, можно до некоторой степени объяснить, почему емкость данного проводника увеличивается при приближении к нему другого проводника. С этою целью обратимся сначала к рис. 123, на котором изображен заря­женный шар А, расположенный внутри металлического сосуда В. Положительный заряд на внешней поверхности сосуда, не связан­ный с электрическим полем внутри сосуда и при установившемся состоянии системы, не имеющей никакого к нему отношения, мы можем отвести в землю, соединив сосуд с нею соответственным проводником. Обозначая через C₁ емкость конденсатора, образуемого шаром А и сосудом В при данном расположении их друг относи­тельно друга, через Q — заряд, находящийся на каждом из провод­ников, и через U _{A '} и U _B' — их потенциалы, можем написать:

Q= С1(U _A' -U _{B '}).

Разность потенциалов U _A' -u _{b '} будем определять как линейный интеграл электрической силы, взятый между А и В вдоль горизон­тального пути, являющегося при данном расположении электродов кратчайшим расстоянием между ними, т. е. имеем:

Представим себе теперь, что шар А опущен вниз (рис. 128) благодаря, например, удлинению шелковой нити, на которой он подвешен, и при этом расстояние между шаром и дном сосуда В стало очень малым по сравнению с прежним. Заряд Q при этом остается неизменным, но общий характер электрического поля сильно изменится вследствие перераспределения фарадеевских тру-

бок. Действительно, стремление трубок сократится, повлечет за. собою перемещение ихкнизу и скопление их в узком промежутке между шаром А и дном сосуда. Они все собрались бы здесь внизу, если бы этому не был положен известный предел со стороны бокового распора трубок. Так как вследствие неиз­менности заряда Q сохраняется и количество фарадеевских трубок, исходящих из A и заканчивающихся на В, то ясно, что сгущение трубок внизу должно сопровождаться разрежением их в других частях электрического поля внутри ка­меры В, в связи с чем уменьшится и величина электрической силы Е там, где произойдет раз­режение трубок. Таким образом, естественно должна измениться и разность потенциалов между А и В. Именно, она уменьшится. Это легко доказать, рассматривая и в данном случае эту разность потенциалов, как линейный интеграл электрической силы вдоль горизонтального же пути между А и В (как и в предыдущем случае):

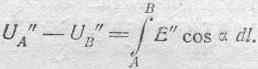
Так как путь интегрирования в первом и во втором случаях один и тот же и в то же время для соответствующих точек будем

иметь

Е"<Е',

то, следовательно:

u_a"-u_b"<u_a'-u_b'.

Обозначая емкость конденсатора во втором случае (рис. 128) через С2, имеем:

Q=C₂(U_A"-U_B").

Принимая во внимание только-что указанное соотношение между разностями потенциалов в обоих случаях, получаем:

С₂>C₁.

Если бы во втором случае мы сообщили нашей конденсаторной системе ту же разность потенциалов, которая была вначале, то очевидно, что заряд на шаре А возрос бы пропорционально возра­станию емкости, и при этом увеличилось бы количество фарадеевских трубок, вмещающихся в рассматриваемой системе. Таким образом, емкость конденсатора можно определить численно, как количество фарадеевских трубок, вмещающихся в диэлектрике конденсатора, когда разность потенциалов между его обкладками раина единице.

Соотношения, выясненные нами при сравнении случаев, изобра­женных на рис. 123 и 128, и соображения, которыми мы руковод-

ствовались, сохраняют свою силу во всех случаях. При этом данное нами определение емкости, как вместимости фарадеевских трубок при единичной разности потенциалов, приложимо ко всем конден­саторам.

Выше было уже упомянуто, что величина емкости зависит от свойств среды, в которой образовано электрическое поле. Фарадей на опыте показал, что величина заряда конденсатора, между элек­тродами или пластинами которого поддерживается постоянная раз­ность потенциалов, зависит от природы диэлектрика, заполняющего пространство между пластинами. Если это пространство заполнено, например, серой или парафином, то заряд получается больше, чем в том случае, когда это пространство ничем не заполнено. Следо­вательно, при прочих равных условиях емкость конденсатора в первом случае больше, чем во втором. Особое свойство диэлект­рика увеличивать ёмкость конденсатора обычно характеризуют отношением емкости С конденсатора, у которого все пространство между пластинами заполнено данным диэлектриком, к емкости С₀ того же конденсатора, когда между его пластинами находится пустота. Отношение это в абсолютной электростатической системе численно равно диэлектрической постоянной среды.

Эта постоянная, как мы знаем, обозначается через e. Вообще всегда имеет место соотношение:

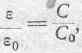
на основании чего можем написать:

где e₀ — диэлектрическая постоянная пустоты, в абсолютной электро­статической системе принимаемая равной единице.

Геометрические размеры конденсатора и диэлектрическая посто­янная той среды, которая находится между пластинами или элек­тродами, вполне определяют его емкость. В целом ряде случаев, имеющих большое практическое значение, емкость конденсатора может быть найдена путем расчета, который по существу сводится к решению задачи об определении разности потенциалов между электродами конденсатора по заданным зарядам и геометрическим размерам.

Дата добавления: 2014-11-29