Энергия электрического поля

Выше было в достаточной степени выяснено (§§ 1 и 47), что, согласно воззрениям Фарадея и Максвелла, в пространстве, в котором существует электрическое поле, среда находится в особом вынужденном состоянии. На создание этой электрической деформации среды всегда должка быть затрачена некоторая работа за счет внешнего деятеля, создающего электрическое поле. Так как в процессе создания электрического поля обычно приходится иметь дело с заряжением отдельных частей системы, т. е. с появлением на этих частях электрических зарядов того или иного знака, и так как работа перемещения какого-либо количества электричества в электрическом поле зависит от потенциалов в различных точках поля, то энергию системы наэлектризованных тел можно формально выразить в зависимости от накопленных количеств электричества и потенциалов различных частей системы, рассуждая при этом так, как будто бы эта энергия тесно связана с наэлектризованными телами. В действительности, однако, эта энергия распределена по всему объему диэлектрика, окружающего наэлектризованные тела, и это именно и есть энергия деформации диэлектрика. Макс­велл доказал правильность такого толкования этого вопроса. Он показал, что выражение для энергии электрического поля, пред­ставленное в виде функции от зарядов и потенциалов всех частей системы, можно преобразовать в выражение, представляющее собою объемный интеграл, распространенный по всему электрическому полю и зависящий от величин, характеризующих электрическую деформацию среды.

Чтобы найти интересующие нас выражения для энергии элек­трического поля, определим прежде всего работу, которая должна быть совершена внешним деятелем для того, чтобы зарядить электризуемую систему путем надлежащих перемещений соответ­ствующих количеств электричества,

Работа, затрачиваемая на перенесение количества электричества dq из бесконечности (или из некоторого места, где потенциал равен нулю) в данную точку, потенциал которой есть U, будет равна, согласно определению потенциала (§ 58), Udq. Результатом этой операции будет увеличение заряда данной части системы на dq, так что, если он перед тем был равен q, после переноса он станет равным q + dq. Мы можем, таким образом, выразить работу, совер-

шаемую во время некоторого определенного изменения зарядов системы, через посредство интеграла:

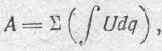
где суммирование (S) должно быть распространено на все элек­тризуемые тела данной системы.

Если U есть потенциал в данной точке, определяемый системою зарядов, которые мы можем обозначить через S q и U' есть потен­циал в той же точке, определяемый другою системою зарядов, которую мы обозначим через S q ', то потенциал в данной точке, зависящий от обеих систем зарядов, существующих одновре­менно, будет равен U+U'. Таким образом, если каждый из за­рядов системы изменяется в отношении n к 1, потенциал в любой данной точке в системе будет также изменяться в отношении n к 1.

Представим себе теперь, что процесс заряжения системы про­изводится следующим образом. Пусть система сначала будет со­вершенно свободна от каких бы то ни было зарядов, и потенциалы всех точек будут равны нулю. Пусть затем различные части системы начинают заряжаться одновременно и все в одном и том же от­ношении к окончательному значению каждого заряда. В таком случае, если q есть окончательный заряд и U— окончательный потенциал некоторой части системы, то величину заряда в некоторой промежуточной стадии можем обозначить через nq и соответствую­щий потенциал — через nU, причем самый процесс электризации можем представить, сделав предположение, что n возрастает непре­рывно от 0 до 1. В то время как n возрастает от n до n+dn, любая часть системы, окончательный заряд которой есть q и окончательный потенциал есть U, приобретает заряд, равный qdn, причем потенциал есть nU. Следовательно, работа, совершаемая в продолжение этой частичной операции, равна qUndn.

Таким образом, полная работа, совершаемая за время заряжения системы, будет равна:

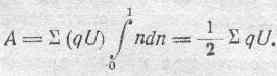
Ясно, конечно, что величина

есть не что иное, как именно электрическая энергия системы, выраженная через заряды различных частей системы и их потен­циалы.

Рассмотрим теперь, каким образом энергия системы наэлектри­зованных тел может быть представлена в виде энергии, распреде-

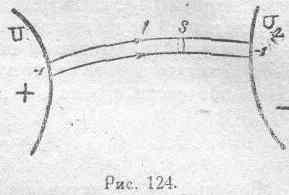
ленной по всему объему диэлектрика. Остановимся на некоторой фарадеевской трубке, находящейся в данном электрическом поле. Эта трубка составляет одно целое с двумя единичными зарядами, нахо­дящимися на концах трубки и учитываемыми полностью при том суммировании членов вида qU, о котором идет речь в только-что выве­денном соотношении (52). Из общего запаса электрической энергии в рас­сматриваемой системе на долю ка­ждой фарадеевской трубки должна быть отнесена именно та часть, которая определяется зарядами и потенциалами концов ее. Рассчитаем теперь эту энергию А_р, приписываемую одной фарадеевской трубке. Допустим, что потенциалы в начале и в конце данной трубки (рис. 124) будут равны соответ­ственно U ₁и U₂, а, длина трубки есть l.

На основании (52) можем написать:

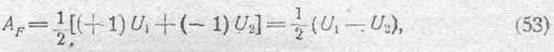
т. е. на долю каждой фарадеевской трубки приходится количе­ство энергии, численно равное половине разности потенциалов между началом и концом трубки.

Заменяя разность потенциалов линейным интегралом электри­ческой силы вдоль фарадеевской трубки, получаем:

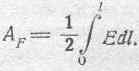
Дифференцируя это выражение по верхнему пределу, получаем количество энергии, которою обладает элемент длины фарадеевской трубки, а именно:

Пользуясь последним соотношением (54), мы можем прежде всего получить количество энергии Ар, рассчитанное на единицу длины фарадеевской трубки. Для этого делим обе части данного соотношения на dl. Мы получим таким путем искомую величину А_F'' , которая с формальной стороны представляет собою не что иное, как производную oт A_F по l

Полученное соотношение гласит, что количество энергии, отне­сенное к.единице длины фарадеевской трубки, численно равно

половине электрической силы в той точке поля, где находится рассматриваемый элемент длины фарадеевской трубки.

Из того же соотношения (54) мы можем еще получить, выраже­ние для энергии электрического поля, отнесенной к единице объема диэлектрика (A₁). Действительно, если обозначить через s сечение фарадеевской трубки в данной точке поля, то элементарный объем участка трубки длиною dl представится в виде sdl. Количество же электрической энергии в этом объеме определяется соотношением (54). Деля обе части его на sdl, получим:

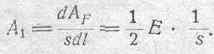
Величина 1/s представляет собою, очевидно, число фарадеевских трубок, проходящих сквозь единицу поверхности уровня в данной точке, т. е..величину электрического смещения D. Одним словом, можем написать (см. соотношение 48):

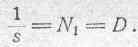
На основании этого получаем окончательно:

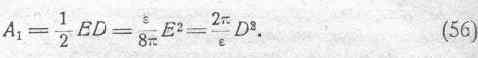
Полученное соотношение, данное впервые Максвеллом, представляет собою весьма важную характеристику электрического поля. Итак, количество энергии, которое мы должны приписать единице объема диэлектрика, является функцией электрической силы Е в данной точке и электрического смещения D, служащего мерой величины электрической деформации среды. Это выражение энергии может быть представлено и в форме функции от диэлектрической постоянной e, т. е. в виде явной функции от физических свойств среды.

Так как соотношение (56) представляет собою результат, непо­средственно вытекающий из выражения (52), то можем, следова­тельно, написать:

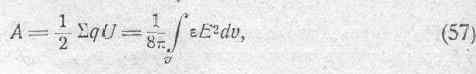
т. е. энергию системы наэлектризованных тел можно предста­вить как энергию, распределенную по всему объему диэлектрика, в котором существует электрическое поле.

Дата добавления: 2014-11-29