Вторая формулировка теоремы Максвелла

Так как электрическое смещение сквозь поперечное сечение фарадеевской трубки равно единице, то, следовательно, каждая такая трубка, пересекая некоторую поверхность, привносит в вели­чину полного электрического сме­щения сквозь эту поверхность свою долю, численно равную единице. Таким образом, в однородном электрическом поле смещение D внекоторой точке А (рис. 120)

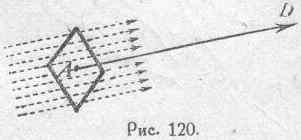
численно равно количеству фарадеевских трубок, проходящих сквозь квадратный сантиметр поверхности, нормальной к вектору D (см. пунктирные линии на рис. 120). Обозначая через N ₁ указанное количество трубок, можем поэтому написать:

d=n ₁. (48) В случае неоднородного поля соотношение (48) примет вид:

D=dN/ds (49)

где dN есть количество фарадеевских трубок, проходящих сквозь элементарную площадку ds, нормальную к вектору D.

Вообще полное электрическое смещение сквозь любую поверх­ность выразится на основании вышеизложенного полным количе­ством (N) фарадеевских трубок, пересекающих рассматриваемую поверхность, т. е.

/ Dcosads=N. (50)

При подсчете числа N мы должны суммировать трубки алгебраи­чески, другими словами, необходимо обращать внимание на то, в каком направлении они пересекают поверхность. Все фарадеевские трубки, пересекающие поверхность в направлении избранной нор­мали к ней, считаются положительными; трубкам же, пересекающим ее в обратном направлении, приписываем знак минус.

Пользуясь соотношением (50) и прилагая его к произвольной замкнутой поверхности, мы можем сформулировать теорему Макс­велла (см. соотношение 31 в § 50) на языке фарадеевских трубок следующим образом:

N=Q, (51)

т. е. полное число фарадеевских трубок, пересекающих некоторую замкнутую поверхность в направлении внешней нормали, равно количеству электричества, находящегося внутри этой поверхности.

Для пояснения новой фор­мулировки теоремы Максвел­ла рассмотрим пример, представленный на рис. 121.

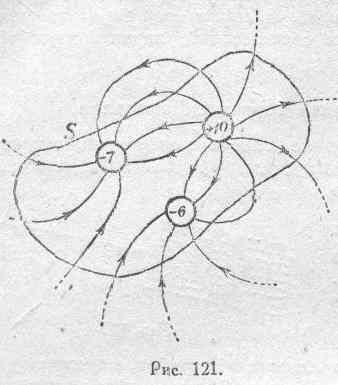
Здесь внутри замкнутой по­верхности 5 представлены три наэлектризованных тела с зарядами +10, -7 и -6. Ясно, конечно, что число фарадеевских трубок, исходя­щих с поверхности заряженного тела или заканчиваю­щихся на нем, в точности равно числу единиц электри­чества того или иного знака, составляющих заряд этого тела. Подсчитывая количество фарадеевских трубок, пересекающих данную замкнутую поверхность s в направлении внешней нормали, получаем;

N=+6-9=-3.

Полное же количество электричества, находящегося внутри 5, будет:

.Q=+10-7-6=-3,

что и показывает справедливость второй формулировки теоремы Максвелла в приложении к данному частному случаю.

Дата добавления: 2014-11-29