Электродвижущая сила и разность потенциалов. Закон электродвижущей силы

Рассмотрим в некотором электрическом поле две точки, А и В. Линейный интеграл электрической силы вдоль некоторого пути перехода от точки А к точке В, т. е.:

численно равен работе электрических сил поля при перенесении единицы положительного электричества из точки А в точку В. Максвелл назвал эту величину полной электродвижущей силой, действующей вдоль данного пути АВ.

Если линия, вдоль которой берется интеграл, образует замкнутый контур и если полная электродвижущая сила e, действующая в этом контуре, не равна нулю, т. е.

в таком случае система не находится в равновесии, и в ней могут возникнуть электрические токи. Эта полная ЭДС, действующая в замкнутом контуре, есть не что иное, как мера внутренней ЭДС, генерируемой в этом контуре. Если рассматриваемый замкнутый контур интегрирования расположен целиком в диэлектрике, вну­тренняя ЭДС может в нем возникнуть, по Максвеллу, только за счет явления электромагнитной индукции. Из опытов Фарадея с полной отчетливостью следует, что величина индуктируемой ЭДС совершенно не зависит от сопротивления цепи. Максвелл, распро­странивший представление о токе и на электрокинетические про­цессы в диэлектриках (см. главу III), по существу предположил, что для любого замкнутого контура, даже если он находится пол­ностью в диэлектрике и является непроводящим в обычном смысле, сохраняет силу основное выражение, определяющее величину ин­дуктированной ЭДС, т. е.

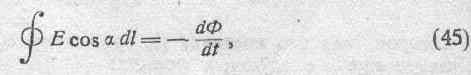
где Ф есть поток, сцепляющийся с данным контуром. В этом утвер­ждении заключается одно из главных положений Максвелла,

касающихся электромагнитного поля. Это соотношение (45), пони­маемое в вышеуказанном общем смысле, мы будем называть зако­ном электродвижущей силы.

В электростатическом поле полная ЭДС внутри какого угодно замкнутого контура равна нулю, т. е.

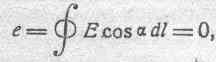
так что, если А и В суть две точки на этом контуре, полная ЭДС, действующая между этими точками, будет одна и та же вдоль лю­бого из двух путей, на которые разбивается контур. Так как далее каждый из этих путей может быть изменяем независимо от другого, полная ЭДС между точками А и В остается неизменною для всех путей перехода от А к В. В рассматриваемом случае полная ЭДС называется разностью потенциалов между точками А к В, т. е

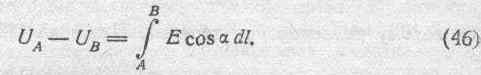
Соотношение (46), определяющее разность потенциалов между точками А к В, как линейный интеграл электрической силы, взятый вдоль любого пути между этими точками, находится в полном со­ответствии с определением потенциала, данным в пункте „д" преды­дущего параграфа 58. Действительно,

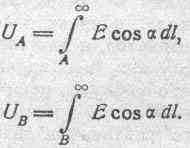
Принимая во внимание, что в данном случае величина линейного интеграла не зависит от пути перехода, можем написать:

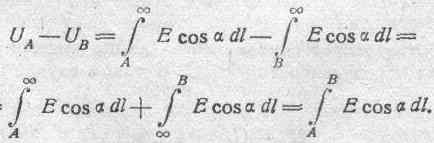
Тело, заряженное положительно, стремится двигаться от мест большего положительного к местам меньшего положительного потен­циала или к местам с отрицательным потенциалом. Всякое же тело, заряженное отрицательно, стремится двигаться в обратном напра­влении.

В проводнике электричество может свободно перемещаться от­носительно проводника. Если, следовательно, две части проводника

обладают разными потенциалами, положительное электричество бу­дет двигаться из мест, имеющих высший потенциал, в места низ­шего потенциала до тех пор, пока существует разность потенциа­лов. Таким образом, проводник может быть в электрическом равновесии только в том случае, когда все части его имеют один и тот же потенциал, называемый потенциалом проводника.

Итак, в электростатическом поле, т. е. в условиях электриче­ского равновесия, имеем для всех точек проводника:

U= const.

Отсюда следует, во-первых, что в этом случае поверхность про­водника является поверхностью уровня, и силовые линии поля нормальны к поверхности проводника. Во-вторых, для всех точек внутри рассматриваемого проводника будет удовлетворяться теорема Лапласа (44):

и потому на основании Теоремы Пуассона (42) получаем:

r=0,

иными словами, внутри проводника, находящегося в состоянии электрического равновесия, не может быть объемного распределения электричества.

Как это явствует из всего, что было сказано в пункте „д":§ 58, в случае многозначности линейного интеграла электрической силы, т. е. в случае, когда величина этого линейного интеграла зависит от пути перехода, понятие о потенциале точки и о раз­ности потенциалов осложняется, и для того, чтобы им пользоваться хотя бы в некоторых случаях, необходимы специальные оговорки. Остановимся прежде всего на случае цепи постоянного тока. Возьмем какие-нибудь точки А и В вдоль проводника. Обычно, в цепях по­стоянного тока принято считать за разность потенциалов между точками цепи А и В то значение интеграла

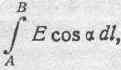
которое соответствует случаю, когда линия интегрирования ни разу не проходит через генератор ЭДС. В таком случае при вычислении

величины:

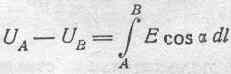
для некоторого участка цепи постоянного тока линия интегриро­вания вся лежит в пространстве, удовлетворяющем условию:

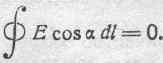
Условию этому именно удовлетворяет вся область установивше­гося электромагнитного поля вокруг проводника, по которому течет постоянный ток. В этом отношении нет никакой разницы между так называемым „электростатическим" полем и электромагнитным полем вне проводника с постоянным током. Из этого, конечно, не следует, что названные два поля и по существу тождественны.

Придерживаясь максвелловской терминологии, мы можем назы­вать электродвижущей силой ту разность потенциалов, которая действует между какими-либо двумя точками цепи постоянного тока. Это соответствует существу дела, так как данная разность потен­циалов, вообще говоря, является причиной, вызывающей ток на данном участке проводника. Для большей точности можно называть разность потенциалов внешней электродвижущей силой, действу­ющей на данном участке проводника. Мы должны при этом строго отличать эту внешнюю электродвижущую силу от внутренних электродвижущих сил, которые могут генерироваться в различных частях цепи тока и которые являются основной причиной возник­новения злектрокинетического процесса в проводящем контуре. Разность потенциалов, действующая на некотором участке цепи постоянного тока, называемая такие иногда электрическим напря­жением или просто напряжением, представляет собою не что иное, как часть основной ЭДС, расходуемую на преодоление со­противлений данного участка. Эти сопротивления могут быть раз­ного рода. Они могут представлять собою обычные электрические сопротивления проводников, входящих в состав цепи. В известных случаях мы встречаемся с обратными ЭДС, действующими внутри данного участка цепи навстречу внешней ЭДС, которая возбуждает электрический ток, преодолевая обратные ЭДС, как некоторое „сопротивление". В частном случае напряжение на зажимах конден­сатора, заряжаемого в какой-либо цепи от внешней ЭДС, имеет характер обратной ЭДС. На основании всего вышеизложенного очевидно, что физическая размерность разности потенциалов и ЭДС одна и та же. Поэтому обе эти величины измеряются одними и теми же единицами, именно, в практической электромагнитной си­стеме — вольтами.

В случае цепи переменного тока, благодаря наличию изменяю­щегося магнитного поля вокруг проводника, нет, вообще говоря, такой области, где величина линейного интеграла электрической силы не зависела бы от выбора пути перехода. Ввиду изложен­ного представление о разности потенциалов, строго говоря, не может применяться при описании явлений, происходящих в цепях переменного тока, и в этом случае следует пользоваться только понятием об ЭДС. Можно говорить об основной переменной ЭДС, генерируемой в альтернаторе или трансформаторе, и об ЭДС, действующей на некотором участке цепи переменного тока, т. е. о напряжении, преодолевающем все сопротивления, какие оказывает цепь на этом участке. Сказанное необходимо иметь в виду, между прочим, во время измерений при помощи вольтметра ЭДС, дей­ствующих в различных частях цепи переменного тока. Так как в

поле такого тока линейный интеграл электрической силы зависит от выбора пути перехода, то ясно, что вспомогательные проводники, при помощи которых вольтметр присоединяется к соответствующим точкам цепи, могут нечто привнести в измеряемую величину и изменить показания вольтметра, причем эти изменения будут за­висеть от общего расположения проводов. В случае низких частот, применяемых в технике сильных токов, описываемое явление столь слабо выражено, что практически оно не имеет существенного зна­чения, и на него обычно не обращают какого-либо внимания. Но в технике высоких частот дело обстоит совсем иначе, и соединитель­ные проводники своим влиянием могут так исказить показания вольтметра, что вопрос о непосредственном измерении ЭДС в высоко­частотных цепях в общей форме надо считать практически нераз­решимым. Такого рода измерения осуществимы только в отдельных частных случаях и с принятием ряда предосторожностей.

Дата добавления: 2014-11-29