Отношения. Декартово произведение множеств

Декартово произведение множеств.

Множество называется декартовым произведением множеств 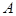и 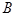(обозначение ), если оно состоит из пар элементов, первый из которые принадлежит множеству 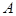, а второй множеству 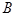. Это обозначается выражением

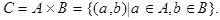
Пример 4.

Дано:

Найти .

Решение:

Заметим, что количество элементов произведения двух множеств равно произведению количеств элементов сомножителей. Это объясняет, почему для этой операции было выбрано название “произведение”.

Можно умножить множество само на себя. Это будет называться декартовым квадратом множества

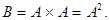
Множество 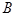в этом случае будет содержать всевозможные пары составленные из элементов множества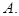

Пример 5.

Дано:

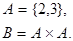
Найти .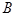

Решение:

Определение отношения очень простое. Отношением на множестве 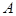называется подмножество декартова квадрата множества :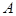

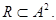
Что это означает содержательно? Рассмотрим группу людей. В психологии есть термин “малая группа”. Это когда в группе от 3 до 30 человек. И попытаемся выяснить, какие отношения у людей в этой группе. Для этого обозначим всю группу буквой 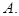Предположим, что в группе 4 человека. Будем обозначать их номерами от 1 до 4. То есть

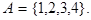
Запишем декартов квадрат множества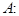

Подмножество 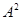тех пар, у которых первый элемент хорошо относится ко второму обозначим 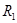. Предположим, например, что

Другое отношение - неприязни

Попробуем прокомментировать эти данные.

Сначала хорошее отношение собранное в 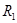. 1-й ко всем относится хорошо, но встречает взаимно хорошее отношение только у 3-го. 2-й хорошо относится к 3-му и,разумеется, к себе тоже. 3-й собой не доволен, а вот 4-й влюблен в себя, и больше ни к кому симпатий не испытывает.

В 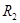- отношение неприязни. 2-й не любит 1. Он считает, что 1 заискивает перед ним, а сам полное ничтожество. 4-й считает, что 1-й вообще настолько ниже него, что его можно не замечать. 2-й не любит и 4-го и пытается обсуждать это с 3, но тот считает, что 2-й его просто достал. У него внутренние проблемы. Он завидует и не любит 4-го, у которого, кажется, никаких проблем нет.

Что можно сказать, о множествах 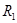и 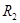? Ясно, что

А может оказаться, что

Может, но не обязательно. Если этого нет, то это означает, что есть еще какие-то отношения или, что существуют такие пары в группе, которые никак друг к другу не относятся. Но это маловероятно.

Дата добавления: 2014-11-28