Модель идеального смешения

Рассмотрим методику составления уравнения модели с учетом химических превращений и переноса вещества движущимся потоком в аппарате идеального смешения. Пусть в аппарате протекает реакция 1-го порядка.

Рис.5.1. Схематическое изображение реактора идеального перемешивания

Составим уравнение материального баланса вещества для этого аппарата.

Входной поток вещества будет равен

(5.1)

Выходной поток вещества будет равен:

(5.2)

Накопление вещества в аппарате за время от 0 до t, будет равно

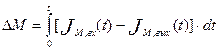(5.3)

Продифференцируем уравнение (5.3) по времени с учетом того, что масса вещества в аппарате будет равна произведению концентрации на объем аппарата, и используем для потоков выражения (5.1) и (5.2):

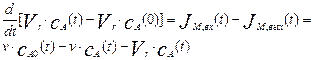(5.4)

Где V_r – объем аппарата в м³.

Учитывая, что в начальный момент времени концентрация в аппарате была постоянной величиной, разделим обе части уравнения (3.4) на объем реактора. В итоге получим следующее уравнение:

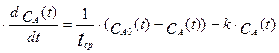(5.5)

Составим теперь уравнение теплового баланса для аппарата идеального смешения. Входной поток тепла равен:

(5.6)

Выходной поток тепла равен:

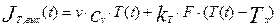(5.7)

Накопление тепла в аппарате равно:

(5.8)

где - накопление тепла в аппарате

Разделим обе части уравнения (5.8) на теплоемкость содержимого аппарата, равную V_r×с_v, где с_v – теплоемкость единицы объема аппарата. После деления продифференцируем обе части по времени и подставим выражения для входящих и выходящих потоков тепла по уравнениям (5.6) и (5.7). В итоге получим:

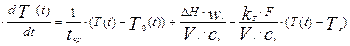(5.9)

Сопоставим теперь полученные дифференциальные уравнения для изменения концентрации и температуры с уравнением математической модели идеального смешения, полученным ранее:

(5.10)

Сравнение показывает, что полученные уравнения материального и теплового баланса отличаются только наличием дополнительных слагаемых, учитывающих поглощение вещества за счет реакции, выделение тепла за счет реакции и теплоотвод за счет теплообмена с окружающей средой. Таким образом, математическую модель технологического аппарата с учетом происходящих химических превращений можно получить из модели структуры потоков путем прибавления к ней так называемых источниковых членов, учитывающих выделение или поглощение данного вещества. При этом изменение температуры описывается также как и изменение концентрации на основе аналогии между переносом тепла и массы.

При этом, следует отметить, что если в аппарате происходят гетерогенные химические процессы, то необходимо, используя квазигомогенную модель, записать скорости гетерогенных процессов как объемные источники или стоки, как было показано в предыдущем разделе.

Таким образом, на основе изложенного, можно записать математические модели аппаратов с учетом процессов химических превращений и теплообмена с использованием различных моделей структуры потоков. При этом если в процессе превращения данный компонент образуется, соответствующий положительный член называется источником. Если соответствующий компонент расходуется, то соответствующий член называется стоком. Для модели идеального вытеснения модель объекта, в котором протекают j=1,…,N_p реакций между i=1,…,K компонентами, уравнения модели будут получены из модели структуры потоков идеального вытеснения в следующем виде:

5.2.Модель идеального вытеснения:

,

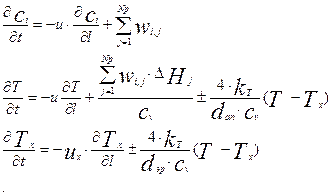(5.12)

С начальными и граничными условиями:

(5.13)

Где: сi – концентрация i-го компонента, wij- скорость расхода (или образования) i-го компонента в j-й реакции. DНj – тепловой эффект j-й реакции

T- температура в реакционной зоне, К, Т_х –температура в теплообменной рубашке, К. k_T- коэффициент теплопередачи, кВт/(м²×К)

d_ап- диаметр аппарата, d_эр – приведенный диаметр поперечного сечения теплообменной рубашки

Дата добавления: 2014-11-29