Основні положення

Розділ 2. ОСНОВИ ТЕОРІЇ ГРАФІВ

Теорію графів почали розробляти для розв'язання деяких задач про геометричні конфігурації, що складаються з точок і ліній.

Визначення графа можна дати як сукупності двох множин V(точок) і E (ліній, дуг), між елементами яких визначене відношення інцидентності, причому кожний елемент е Î E інцидентний двом елементам v', v" Î V. Елементи множини V називаються вершинами графа G, елементи множини Е - його ребрами. Вершини і ребра графа G називають ще його елементами і замість е Î Е і v ÎV пишуть e Î G і v Î G.

У деяких графах інцидентні ребру вершини нерівноправні, вони повинні, наприклад, розглядатися у визначеному порядку. Тоді кожному з ребер можна приписати напрямок від першої із інцидентних вершин до другої. Спрямоване ребро часто називають дугою, а граф, що їх містить, - орієнтованим. У противному випадку (інцидентні ребру вершини рівноправні) граф будемо називати неорієнтованим.

Початок Кінець

1 2

Дуга: виходить входить

Рис.2.1. Зображення орієнтованого графа:

1-дуга виходить; 2-дуга входить.

Наочне уявлення про граф можна одержати, якщо уявити собі деяку множину точок площини Х, що називаються вершинами, і множину спрямованих відрізків U, що з'єднують усі або деякі з вершин і називаються дугами. Математично граф G можна визначити як пару множин Х і U: G = (X, U). Граф називається повним, якщо дві різні його вершини з'єднані лише одним ребром.

На рис. 2.2 зображений граф, вершинами якого є точки a, b, c, d, e, g, h, а дугами - відрізки (a, a), (c, b), (c, d), (c, e), (d, c), (d, d), (e, d), (g, h).

Рис.2.2. Зображення графа

Прикладами графів є відношення батьківства і материнства на множині людей (дерево родоводу), карта доріг на місцевості, схема з'єднань електричних приладів, відношення переваги одних учасників турніру над іншими і т.п. Іноді буває зручно дати графу інше визначення. Можна вважати, що множина спрямованих дуг U, які з'єднують елементи множини Х, відображає цю множину саму в себе. Тому можна вважати граф заданим, якщо дана множина його вершин Х і спосіб відображення Г множини Х в Х. Таким чином, граф G є пара (Х, Г), що складається з множини Х і відображення Г, заданого на цій множині G=(X, Г).

Так, для графа, зображеного на рис.2.2, відображення визначається в такий спосіб:

Гa=a; Гb=Æ; Гc={b, d, e}; Гd={c, d}; Гe=d; Гg=h; Гh=Æ.

Неважко помітити, що дане визначення графа цілком збігається з визначенням відношення на множині.

Введемо деякі поняття і визначення, необхідні для опису різноманітних видів графів.

Підграфом G_A графа G=(X, Г) називається граф, в який входить лише частина вершин графа G, що утворює множину А, разом із дугами, що з'єднують ці вершини, наприклад обкреслена пунктиром область А на рис.2.2. Математично підграф позначається в такий спосіб:

G_A=(A,Г_A), де АÍХ, Г_АХ=(Г_Х)ÇА.

Частковим графом G_D стосовно графа G=(X, Г) називається граф, що містить тільки частину дуг графа G, тобто визначений умовою:

G_D=(X, D), де Dx Í Г_X.

Наприклад, нехай G=(X, Г) - карта шосейних доріг України. Тоді карта шосейних доріг Дніпропетровської області являє собою підграф, а карта головних доріг України - це частковий граф.

Іншими важливими поняттями для графа є поняття шляху і контуру. Дуга, що з'єднує вершини a і b, спрямована від а до b і позначається u=(a, b).

Визначення

Шляхом у графі G називають таку послідовність дуг m=(u₁,...,u_k), в якій кінець кожної попередньої дуги збігається з початком наступної. Шлях m, послідовними вершинами якого є вершини a, b,..., m, позначається через m=(a, b,..., m).

Довжиною шляху m=(u₁,...,u_k) називають число l(m)=k, що дорівнює числу дуг, які складають шлях. Іноді кожній дузі u_i приписують деяке число l(u_i), яке називається довжиною дуги. Тоді довжина шляху визначається як сума довжин дуг, що складають шлях

_k

l (m)=S l(u_i).

^I=1

Шлях, в якому ніяка дуга не зустрічається двічі, називається простим. Шлях, в якому ніяка вершина не зустрічається двічі, називається елементарним.

Контур - це кінцевий шлях m=(x₁,..., x_k), де початкова вершина х₁ обов'язково збігається з кінцевою х_k. При цьому контур називається елементарним, якщо всі його вершини різноманітні (за винятком початкової і кінцевої, що збігаються). Контур одиничної довжини, утворений дугою вигляду (а, а), називається петлею. Так, на рис.2.2 (e, d, c, b) - шлях, а (c, e, d, c) - контур, (d, d) - петля. 1 (e, d, c, b) - шлях, а (c, e, d, c) - контур, (d, d) - петля.

Іноді графи зручно подавати у вигляді матриць, зокрема у вигляді матриць суміжності та інцидентності. Попередньо дамо два визначення.

Вершини x і y є суміжними, якщо вони різноманітні і якщо існує дуга, що йде з x до y.

Дугу u називають інцидентною вершині х, якщо вона заходить у цю вершину або виходить з неї.

Позначимо через х₁,..., х_n вершини графа, а через u₁,...,u_m - його дуги. Введемо числа:

ì 1, якщо є дуга, що з'єднує вершину i із вершиною j; r_ij = í

î 0, якщо такої дуги немає.

Квадратна матриця R=[r_ij] порядку (n x n) називається матрицею суміжності графа.

Введемо числа:

ì +1, якщо u_j виходить із x_i ;

S_ij = í -1, якщо u_j заходить у x_i ;

î 0, якщо u_j не інцидентна x_i.

Тоді матриця S=[S_ij] порядку (n x m) називається матрицею інцидентності для дуг графа.

Матриці інцидентності в описаному вигляді застосовні тільки до графів без петель. У випадку наявності в графі петель цю матрицю варто розчленувати на дві півматриці: позитивну і негативну.

На рис.2.3 наведений граф без петель, для якого матриці суміжності та інцидентності мають такий вигляд:

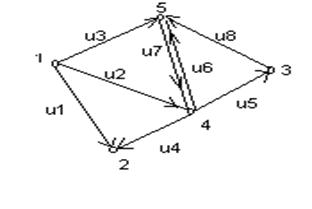Матриця суміжності

I, J 1 2 3 4 5

1 0 1 0 1 1

2 0 0 0 0 0

Рис. 2.3. Граф без петель

3 0 0 0 0 1

4 0 1 1 0 1

5 0 0 0 1 0

Звичайно графи, які розглядаються, є кінцевими, тобто кінцеві множини їхніх елементів (вершин і ребер). Тому скінченність цих графів не буде додатково визначатися.

Приклади орієнтованих графів показані на рис.2.4.

Матриця інцидентності

i j
	-1			-1
					-1
		-1					-1
			-1			-1		-1

а b с

d e f g к

(кратне ребро)

Рис.2.4. Приклади орієнтованих графів

В наведених прикладах варіант "b" подає граф із порожньою множиною ребер. Граф "е" ілюструє недосяжність двох вершин, а "g" - граф із петлею.

Дата добавления: 2014-11-29