Неорієнтовані графи

Іноді граф розглядають без урахування орієнтації дуг, тоді його називають неорієнтованим графом. Поняття "дуга", "шлях" і "контур" для неорієнтованого графа заміняються поняттями "ребро", "ланцюг", "цикл". Ребро - це відрізок, що з'єднує 2 вершини. Ланцюг - послідовність ребер. Цикл - ланцюг, у якого початкова і кінцева вершини збігаються. Описати неорієнтований граф можна шляхом завдання пари множин (Х, U), де Х - множина вершин; U - множина ребер. Проте більш зручним є опис неорієнтованого графа за допомогою матриці суміжності або інцидентності, що будуються аналогічно відповідним матрицям для орієнтованих графів з тією різницею, що не робиться різниця між дугами, які входять у вершину і виходять з неї. При цьому вершини х і y називають суміжними, якщо існує ребро, що їх з'єднує, і це ребро називається інцидентним вершинам х і у.

Наведемо ще декілька визначень, які використовуються для характеристики неорієнтованих графів.

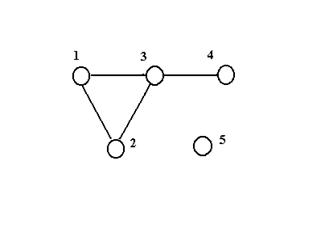
Ступенем вершини х, що позначається deg(x) або dx, називають число ребер, інцидентних вершині х. Так, для графа на рис.2.5 маємо d1=2, d2=2, d3=3, d4=1, d5=0. Якщо dx=1, то вершину називають тупиковою; якщо dx=0 то вершину називають ізольованою.

Рис.2.5. Неорієнтований граф

Теорема. Нехай G - неорієнтований граф із n вершинами та m ребрами і d_j - ступінь j-й вершини. Тоді Sn_j= 1 і d_j=2m.

Доказ теореми випливає з того, що кожне ребро добавляє одиницю до ступеня кожної з 2-х вершин, що воно з'єднує, тобто добавляє 2 до суми ступенів уже наявних вершин.

Таким чином у кожному графі число вершин непарного ступеня парне.

Для неорієнтованого графа поняття "підграф" і "частковий граф" аналогічні відповідним поняттям для орієнтованого графа.

З поняттям неорієнтованого графа пов'язана важлива характеристика, що називається зв'язністю графа. Кажуть, що граф зв'язний, якщо будь-які дві його вершини можна з'єднати ланцюгом. Якщо граф G не зв'язковий, то його можна розбити на такі підграфи G_i, що усі вершини в кожному підграфі зв'язні, а вершини з різноманітних підграфів не зв'язні. Такі підграфи G_i називають компонентами зв'язності графа G. Якщо з графа (рис.2.5) виключити ізольовану вершину 5, то отриманий граф буде зв'язним. Граф на рис.2.6 не зв'язний і має дві компоненти зв'язності.

Його можна перетворити в зв'язний, додавши ребро (міст), що з'єднує вершини 3 і 5 (штрихова лінія). Видалення моста перетворює зв'язний граф у незв'язний.

Для того щоб визначити зв'язність орієнтованого графа, не потрібно звертати увагу на орієнтацію дуг. Граф, зображений на рис.2.6, є не зв'язним.

Рис.2.5 – Незв'язний граф

Проте його підграф, що складається з вершин 1, 2, 3, 4 є зв'язним. Для орієнтованого графа існує поняття сильної зв'язності. Граф сильно пов'язаний, якщо для будь-яких 2-х вершин х і у існує шлях, що йде з х в у. Важливий окремий випадок неорієнтованого графа - дерево (рис.2.7).

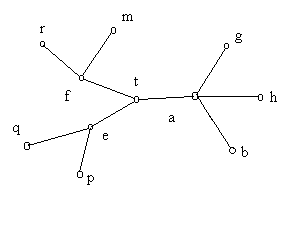
Деревом називають кінцевий зв'язковий неорієнтований граф, що не має циклів. Якщо дана множина вершин a, b, c,..., то дерево можна побудувати таким чином. Одну з вершин, наприклад а, приймемо за початкову і назвемо її 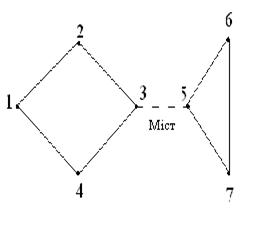коренем дерева.

Рис.2.6. Незв'язаний граф

З цієї вершини проводимо ребра в сусідні вершини b, c, d,..., із них проводимо ребра в сусідні з ними вершини c, f, g, h,... і т.д. Отже, дерево можна побудувати послідовно, додаючи ребра в його вершинах. Це дає можливість установити зв'язок між числом вершин і числом ребер дерева. Найпростіше дерево складається з 2-х вершин, що з'єднані ребром. Щораз коли ми добавляємо ще одне ребро, наприкінці його додається і вершина. Отже, дерево з n вершинами має n - 1 ребер.

Дата добавления: 2014-11-29