
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы теории множеств
Алгебра высказываний (булева алгебра)
Математические основы информатики
Основное понятие булевой алгебры – выказывание. Под простым высказыванием понимается повествовательное предложение, о котором можно сказать, истинно оно или ложно, поэтому высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (0) или ИСТИНА (1). Например, содержание высказывания А: «дважды два равно четырем» истинно А = 1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ. В дальнейшем нас не будет интересовать содержательная часть высказываний, а только их истинность. Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, записывается А = В.
Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций. Рассмотрим их подробней.
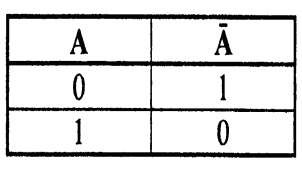 Операцией отрицания А (Ø А, не А) называют высказывание А, которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то Ø А - «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание – унарная (т.е. для одного операнда) логическая операция.
Операцией отрицания А (Ø А, не А) называют высказывание А, которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то Ø А - «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание – унарная (т.е. для одного операнда) логическая операция.
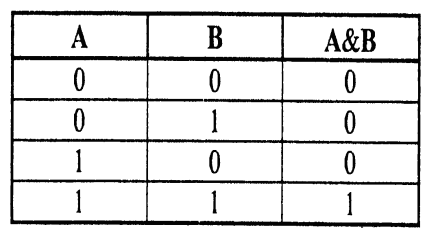 Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается С = А Ù В или С = А & В (С равно А и В). Например, пусть высказывание А «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери».
Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается С = А Ù В или С = А & В (С равно А и В). Например, пусть высказывание А «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери».
 Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается С = A Ú В (С равно А ИЛИ В). Пример: высказывание А «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе».
Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается С = A Ú В (С равно А ИЛИ В). Пример: высказывание А «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе».
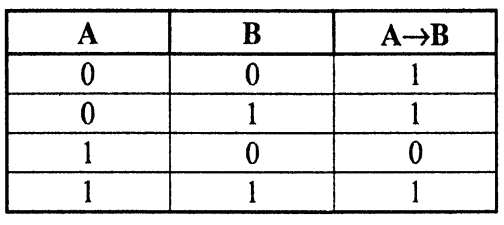
Импликацией двух высказываний А (А - посылка) и В (В - заключение) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается С = А ® В (из А следует В). Пример: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи». Операция не симметрична, т.е. из В ® А не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.
Эквиваленцией двух высказываний А и В является новое вы  сказывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается С = А «В (С = А º В).
сказывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается С = А «В (С = А º В).
С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические
выражения, которые также называются булевскими функциями. Например, С = ((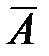 Ú В) ® В) Ú А. Чтобы избежать большого количества скобок в булевских функциях, принято соглашение о старшинстве операций. Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.
Ú В) ® В) Ú А. Чтобы избежать большого количества скобок в булевских функциях, принято соглашение о старшинстве операций. Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.
Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истинности следующие равносильности:
1. 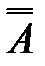 = А = А
| закон двойного отрицания |
| 2. А & В = В & А | коммутативный закон для конъюнкции |
| 3. A Ú B = B Ú A | коммутативный закон для дизъюнкции |
| 4. (А & В) & С = А & (В & С) | ассоциативный закон для конъюнкции |
| 5. (A Ú B) Ú C = A Ú (B Ú C) | ассоциативный закон для дизъюнкции |
| 6. А & (В Ú С) = (А & В) Ú (А & С) | дистрибутивные законы |
| 7. A Ú (В & С) = (A Ú В) & (A Ú С) | |
8. 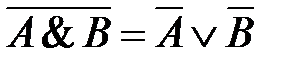
| законы де Моргана |
9. 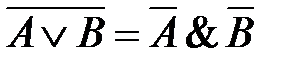
| |
| 10. А & А = А | закон идемпотенции для конъюнкции |
| 11. A Ú A = А | закон идемпотенции для дизъюнкции |
| 12. А & 1 = А | закон единицы для конъюнкции |
| 13. А & 0 = 0 | закон нуля для конъюнкции |
| 14. A Ú 1 = 1 | закон единицы для дизъюнкции |
| 15. A Ú 0 = А | закон нуля для дизъюнкции |
16. A Ú 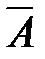 = 1 = 1
| закон исключения третьего |
17. А & 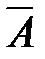 = 0 = 0
| закон противоречия |
18. А ® В = 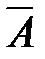 Ú В Ú В
| |
19. А «В = (А ® В) & (В ® А) = (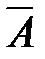 Ú В) & (A Ú Ú В) & (A Ú 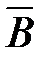 ) = (A & B) Ú ( ) = (A & B) Ú (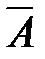 & & 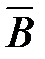 ) )
| |
| 20. A Ú (А & В) = А | законы поглощения |
| 21. А & (A Ú В) = А | |
22. А & (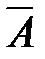 Ú B) = A & B Ú B) = A & B
| |
23. A Ú (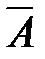 & В) = A Ú В & В) = A Ú В
|
Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь возможность приводить формулы с помощью эквивалентных преобразований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований.
Первая из них – дизъюнктивная нормальная форма (ДНФ), имеет вид A l Ú A 2 Ú... Ú An, где каждое из составляющих высказываний есть конъюнкция простых высказываний и их отрицаний, например:
В = ( & А 2 & A 3) Ú (А 4 & А 5).
& А 2 & A 3) Ú (А 4 & А 5).
Вторая – конъюнктивная нормальная форма (КНФ), имеет вид А 1 Ù А 2 Ù... Ù An, где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний, например:
В = 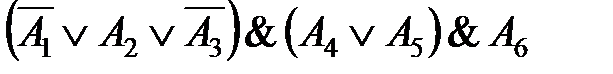 .
.
Множеством называется любое объединение определенных вполне различимых объектов; их может и не быть вообще. Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединенные по любому признаку.
Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, оно обозначается Æ. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным. Задать множество можно перечислением его элементов. Например, множество образованное из n элементов а 1, а 2,..., аn, обозначается А = { а 1, а 2,..., ап }; пишется а Î А, если а является элементом множества А, в противном случае a Ï A. Задать множество можно также, указав общее свойство для всех его и только его элементов.
Два множества считаются равными, если состоят из одних и тех же элементов; записывается этот факт А = В. Множество А 1, называется подмножеством А, если все элементы множества А 1 являются элементами А (записывается А 1 Ì А).
Для множеств определены следующие операции: объединение, пересечение, дополнение. Объединением множеств А и В (записывается A È B) называется множество, состоящее из элементов как одного, так и второго множества. Пересечением множеств А и В (записывается А Ç В) называется множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно. Дополнением множества А до В называется множество, состоящее из элементов множества В, не принадлежащих А. Дополнение обозначается 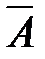 = В – А (рис. 1.7).
= В – А (рис. 1.7).
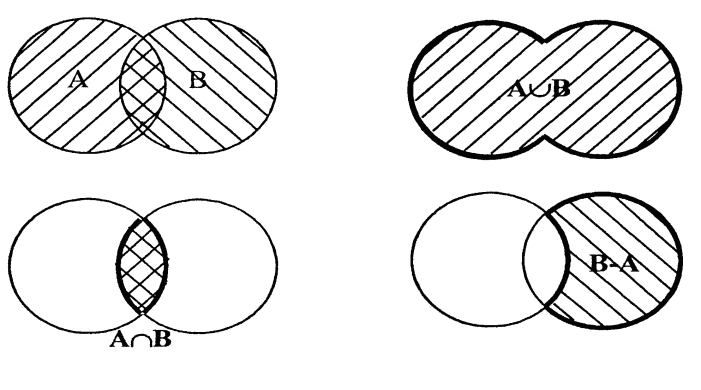
Рис. 1.2. Операции над множествами
|
|
Дата добавления: 2014-11-29; Просмотров: 390; Нарушение авторских прав?; Мы поможем в написании вашей работы!