Системы счисления

Представление (кодирование) данных

Информационные процессы

Получение информации тесно связано с информационными процессами, поэтому имеет смысл рассмотреть отдельно их виды.

Сбор данных – это деятельность субъекта по накоплению данных с целью обеспечения достаточной полноты. Соединяясь с адекватными методами, данные рождают информацию, способную помочь в принятии решения. Например, интересуясь ценой товара, его потребительскими свойствами, мы собираем информацию для того, чтобы принять решение: покупать или не покупать его.

Передача данных – это процесс обмена данными. Предполагается, что существует источник информации, канал связи, приемник информации, и между ними приняты соглашения о порядке обмена данными, эти соглашения называются протоколами обмена. Например, в обычной беседе между двумя людьми негласно принимается соглашение, не перебивать друг друга во время разговора.

Хранение данных – это поддержание данных в форме, постоянно готовой к выдаче их потребителю. Одни и те же данные могут быть востребованы не однажды, поэтому разрабатывается способ их хранения (обычно на материальных носителях) и методы доступа к ним по запросу потребителя.

Обработка данных – это процесс преобразования информации от исходной ее формы до определенного результата. Сбор, накопление, хранение информации часто не являются конечной целью информационного процесса. Чаще всего первичные данные привлекаются для решения какой-либо проблемы, затем они преобразуются шаг за шагом в соответствии с алгоритмом решения задачи до получения выходных данных, которые после анализа пользователем предоставляют необходимую информацию.

Существуют различные способы записи чисел. Совокупность приемов записи и наименования чисел называется системой счисления. Числа записываются с помощью символов. По количеству символов, используемых для записи числа, системы счисления подразделяются на позиционные и непозиционные. Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Примером непозиционной системы счисления может служить римская. Например, для записи числа один используется буква I, два и три выглядят как совокупности символов II, III, но для записи числа пять выбирается новый символ V, шесть – VI, десять – вводится символ X, сто – С, тысяча – М и т.д. Бесконечный ряд чисел потребует бесконечного числа символов для записи чисел. Кроме того, такой способ записи чисел приводит к очень сложным правилам арифметики.

Позиционные системы счисления для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т.е. от позиции, занимаемой цифрой, например, 125 и 215. Количество цифр, используемых для записи числа, называется основанием системы счисления, в дальнейшем его обозначим q.

В повседневной жизни мы пользуемся десятичной позиционной системой счисления, q = 10, т.е. используется 10 цифр. Используя конечное число цифр, можно записать любое сколь угодно большое число. Число в позиционной системе счисления с основанием q может быть представлено в виде полинома по степеням q.

X_(q) = x_{n -1}× q^{n -1} + x_{n -2}× q^{n -2} +…+ x ₁× q ¹ + x ₀× q ⁰ + x_{- 1}× q ^-1 + x _-2× q ^-2 +… x _{- m} × q ^{– m} _.

Здесь X(q) – запись числа в системе счисления с основанием q; х_i – натуральные числа меньше q, т.е. цифры; n – число разрядов целой части; m – число разрядов дробной части.

Записывая слева направо цифры числа, мы получим закодированную запись числа в q -ичной системе счисления:

X_(q) = x_{n -1} x_{n -2}… x ₁ x ₀ x_{- 1} x _-2… x _{- m} .

Основание системы записывается после числа в виде нижнего индекса. Например, одно и то же число 231, записанное в десятичной системе, запишется в двоичной, восьмеричной и шестнадцатеричной системах счисления следующим образом:

231₍₁₀₎=11100111₍₂₎=347₍₈₎=E7₍₁₆₎.

Далее приведена табл. 1.4, содержащая наименования некоторых позиционных систем счисления и перечень знаков (цифр), из которых образуются в них числа.

Таблица 1.1. Некоторые системы счисления

Основание q	Система счисления	Знаки
	Двоичная	0,1
	Восьмеричная	0,1,2,3,4,5,6,7
	Десятичная	0,1,2,3,4,5,6,7,8,9
	Шестнадцатеричная	0,1,2,3,4,5,6,7,8,9,A.B,D,E,F

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, т. к. все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию q системы счисления.

0 + 0 = 0	0 ´0 = 0
0 + 1 = 1	0 ´1 = 0
1 + 0 = 1	1 ´0 = 0
1 + 1 = 10	1 ´1 = 1

В информатике, вследствие применения электронных средств вычислительной техники, большое значение имеет двоичная система счисления, q = 2. Таблица сложения и умножения двоичных чисел:

Преобразование из десятичной в прочие системы счисления проводится с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.

Алгоритм перевода чисел из десятичной системы счисления в систему с основанием q > 1:

1) если переводится целая часть числа, то она делится на q, после чего запоминается остаток от деления. Полученное частное вновь делится на q, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на q выписываются в порядке, обратном их получению;

2) если переводится дробная часть числа, то она умножается на q, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на q и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая дробь в системе счисления с основанием q.

Рассмотрим алгоритм перевода десятичного числа 231 в двоичную систему (аналогично выполняется перевод из десятичной системы в любую q -ичную). Последовательное деление нацело позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа.

231₍₁₀₎ = 1 × 2⁷ + 1 × 2⁶ + 1 × 2⁵ + 0 × 2⁴ + 0 × 2³ + 1 × 2² + 1 × 2¹ +

+ 1 × 2⁰ = 11100111₍₂₎.

Процесс деления записывают следующим образом:

231₍₁₀₎ = 11100111₍₂₎.

Записывая значения частного и остатков от деления в виде нулей и единиц в порядке, обратном вычислению, получим двоичную запись числа.

Для дробных чисел правило последовательного деления заменяется правилом последовательного умножения. Рассмотрим на примере. Переведем 0,8125 из десятичной системы в двоичную систему счисления. Получаем таблицу:

Для выполнения арифметических операций в системе счисления с основанием q необходимо иметь соответствующие таблицы сложения и умножения.

Пример 1. Сложить числа:
а) 10000000100₍₂₎ + 111000010₍₂₎ = 10111000110₍₂₎;
б) 223,2₍₈₎ + 427,54₍₈₎ = 652,74₍₈₎; в) 3B3,6₍₁₆₎ + 38B,4₍₁₆₎ = 73E,A₍₁₆₎.

10000000100 223,2 3B3,6 + 111000010 + 427,54 +38B,4 ------------ ------- ----- 10111000110 652,74 73E,A

Выполним проверку результатов расчетов переводом в десятичную систему счисления. Для этого переведем каждое слагаемое и сумму в десятичную систему счисления, выполним сложение слагаемых в десятичной системе счисления. Результат должен совпасть с суммой.

а) 10000000100₍₂₎=1×2¹⁰+1× 2² = 1024+4=1028₍₁₀₎

111000010₍₂₎=1×2⁸+ 1×2⁷+ 1×2⁶+ 1×2¹ = 256+128+64+2 = 450₍₁₀₎

10111000110₍₂₎ = 1×2¹⁰ + 1×2⁸ + 1×2⁷ + 1×2⁶ + 1×2² + 1×2¹ = 1024 + 256 + 128 + 64 + 4 + 2 = 1478₍₁₀₎

1028₍₁₀₎ + 450₍₁₀₎ = 1478₍₁₀₎

Результаты совпадают, следовательно, вычисления в двоичной системе счисления выполнены верно! Примеры под буквами б) и в) проверьте самостоятельно.

Пример 2. Выполнить вычитание:
а) 1100000011,011₍₂₎ - 101010111,1₍₂₎ = 110101011,111₍₂₎;
б) 1510,2₍₈₎ - 1230,54₍₈₎ = 257,44₍₈₎; в) 27D,D8₍₁₆₎ - 191,2₍₁₆₎ = EC,B8₍₁₆₎.

1100000011,011 1510,2 27D,D8 - 101010111,1 -1230,54 -191,2 -------------- ------- ------ 110101011,111 257,44 EC,B8

Пример 3. Выполнить умножение:

а) 100111₍₂₎ ´ 1000111₍₂₎ = 101011010001₍₂₎.

б) 1170,64₍₈₎ ´ 46,3₍₈₎ = 57334,134₍₈₎. в) 61,A₍₁₆₎ ´ 40,D₍₁₆₎ = 18B7,52₍₁₆₎.

100111 1170,64 61,A *1000111 * 46,3 *40,D ------------- -------------- ---------- 100111 355 234 4F 52 + 100111 + 7324 70 + 1868 100111 47432 0 ---------- 100111 ------------- 18B7,52 ------------- 57334,134 101011010001

Пример 4. Выполнить деление:

а) 100110010011000₍₂₎: 101011₍₂₎=111001000₍₂₎;

б) 46230₍₈₎: 53₍₈₎=710₍₈₎; в) 4C98₍₁₆₎: 2B₍₁₆₎=1C8₍₁₆₎.

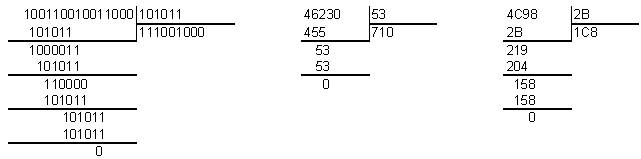
Дата добавления: 2014-11-29