Декартова (Картезианская) система координат

Структура взаимосвязей между системами координат

1) Базовая косоугольная система координат

Координаты определяются осями (х – ось абсцисс, у - ось ординат)

Расстояние определяется проекциями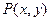

4) Полярная система координат

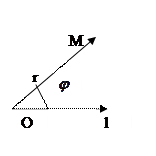
(.)0 – полюс, 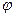- полярный угол, r – полярное расстояние. M(r, )

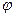Соответственно

6) Цилиндрические координаты

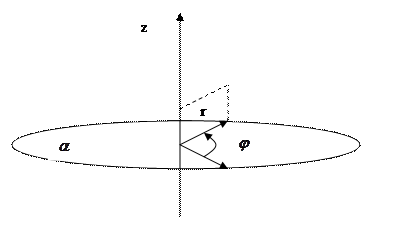Есть некая плоскость

Z проекция на точку M

7) Сферические системы координат

угол 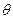- полярное расстояние

угол 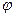- долгота

Соответственно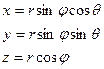

1.

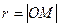
2.

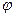
3.

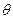
Косоугольная система координат

Декартова система координат	M(x,y,z)
Полярная	M()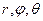
Цилиндрическая	M()
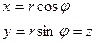
Сферическая с коор.	M()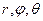

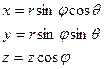
0 в середине экрана у Квартезианст.

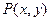(.) Все наши представления в векторах, в виде матрицы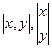

Преобразование в компьютерной графике

- проекционное преобразование

- геометрические (аффинные) преобразования

& Геометрические преобразования в компьютерной графике.

Аффинные преобразования.

Преобразования связанные с некоторыми изменениями объекта.

- Перенос

- Поворот

- Масштабирование

! Св - во аффинных преобразований

Св-во1 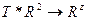всегда переводят прямую Q в T(a) так что множество точек прямой a отображается на множество (.) T(a)

Св-во 2 Если множество прямых а и b параллельны и задано некое аффинное преобразование T(a) и T(b) будут также параллельны

Дополнительные свойства

· Произведение 2-х аффинных преобразований также аффинное преобразование

· Для каждого преобразования Т существует такое Т – 1, которое тоже является аффинным преобразованием.

Рассмотрим последовательно аффинные преобразование.

(!) Масштабирование (scale)

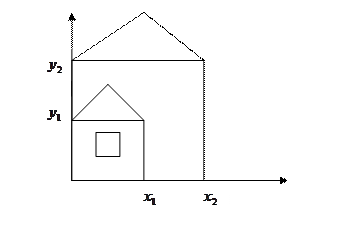
Если имеем

, а 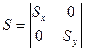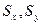- коэф. Мосштабиров.

, то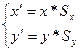

Свойства преобразования масштабирования

- не сохраняется длинна

- не сохраняются углы

(!) Поворот (rotate)

Если то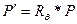

Соответственно матрица поворота

(!) Перенос (Translate)

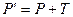
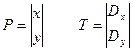
(!) Отражение (Reflection)

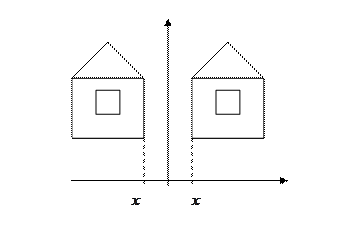
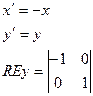
(!) Скос (самостоятельно)

Дата добавления: 2014-11-28