Растяжение и сжатие

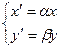
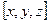
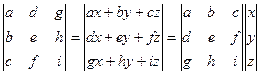
Матрица преобразования в однородной системе координат.

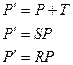Пусть точка М существует на плоскости с координатами (х,у)

Однородной системой координат будет называться 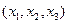связанная с точкой (х,у)

Соотношениями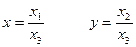

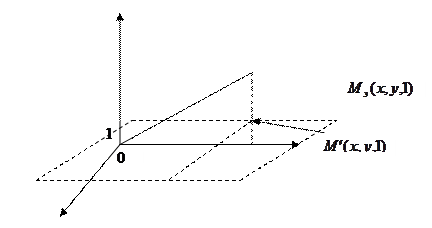
Может быть задана произвольным набором координат

Матрица 3х3 для 2х мерного пространства

Матрица 4х4 для 3х мерного пространства

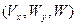
промосштабируем с коэфициэнтом W в 2х мерной плоскости

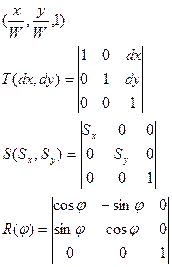
Построить матрицу поворота вокруг произвольной точки на плоскости (a,b)

Шаги:

1) Перенос на вектор 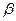= - а – b

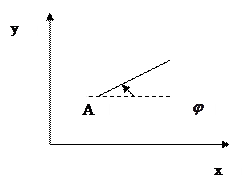
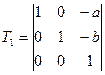
2)Поворот на угол 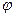начала координат

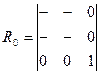
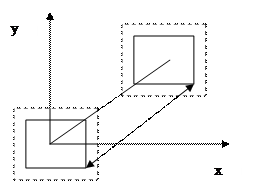3)Перенос в (.) А с координатами

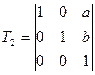
Перенос – Перенос -> коммутативные операции

Масштаб- Масштаб

Поворот- Поворот

Перенос – Масштаб -> некоммутативные операции

Поворот - Перенос

Преобразование в пространстве

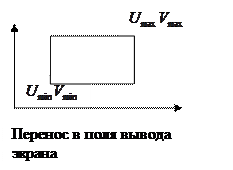
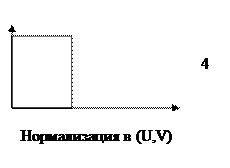
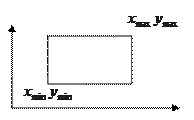
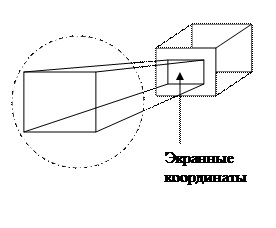Шаги при преобразовании в VP

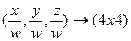
Правосторонняя или левосторонняя по правилу буравчика

Положительными будем считать повороты (если смотреть с конца положительной полуоси в сторону начала координат) при которых поворот на 90 градусов против часовой стрелки будет проводить одну положительную ось на другую.

оси	Положительно б. направлено
x	от y к z
y	от z к x
z	от x к y

1. Перенос

2. Масштаб

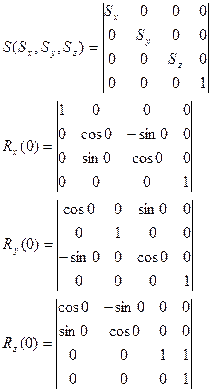
Композиция 3-х мерных преобразований

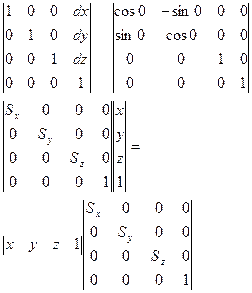
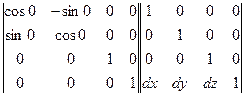
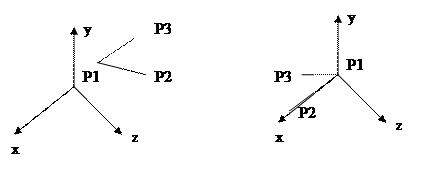
Повор. Вокруг н.к.

Чтобы P1 и P2 совместились с

Осью z

1. Перенос P1 в н.к.:

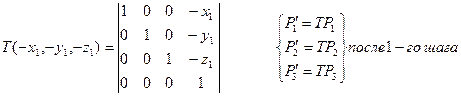
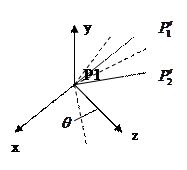
2. Поворот вокруг оси у 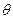- положит., А 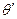– поворот в обратную сторону

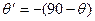
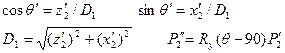
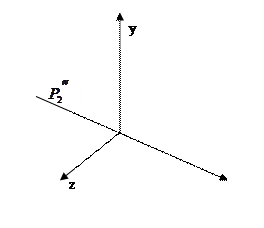
3.Поверн. На угол 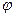относит ос х

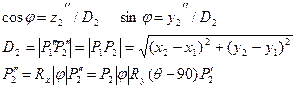
1. Поместить 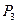в плоскость УОZ – самостоятельно.

Многомерные пространства и проекции

Самая часто встреч.

1. Симметрия отображения (зеркальная симметрия)

2. Поворот Отношение симметр. Своб. К повороту на определенный угол.

Ось поворота – поворотная ось симметрии.

Поворотная ось – ось вокруг которой может осуществить поворот до совмещения с самим собой.

Наименьший угол на который не повернуть – это Элементарный угол. Он определяет порядок, ось симметрии.

f.c. 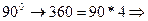4-ый порядок оси симметрии

120 – 3-й порядок.

3. Симметрия переноса – трансляция

Повторяемость фигуры в пространстве осуществляется ч/з некоторое расстояние.

Также называется симметрией 2-го переноса

1. Винтовая симметрия

Происходит перемещение и поворот по определенной траектории

Многогранники – тело, ограниченное определен. количеством поверхностей которые представляет собственные многоугольники.

прим. Призма, пирамида.

Правильный – выпуклый многоугольник обладающий максимальной 3-хмерной плотностью упаковки.

Известно 5 таких многогранников:

Платоново тело	Число сторон у граней	Число ребер у вершин	Число ребер	Число вершин	Общее число ребер
Тетраэдр
Куб (иксаэдр)
Октаэдр
Додекаэдр
Икосоэдр

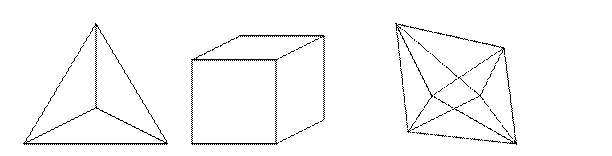
1. Они м. б. построены они из др.
2. Вокруг кажд. м. описать сферу и каждый м. вписать в сферу. Из куба – октоэдр:

Вершина октаэдра – центральный граней куба.

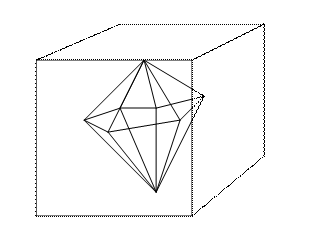
Данные тела обладают симметрией многогранников.

1. Есть центр. Симметрии
2. Существуют плоскости симметрии

- 3 плоскости симметрии перпендикулярны ребрам в их серединах.

- 6 плоскостей симметрии проходящих через противоположные ребра.

3. Оси симметрии

- Существуют оси симметрии 4-го порядка

- они проходят через центры граней

- 6 осей симметрии 2-го порядка – проходят через середины противополож. Ребер

- 4 оси зеркальной симметрии – проходят через середины противоположных ребер.

Аналог м. для всех Платоновых тел

Фрактал

1985 г. (IBM) Красота фрактала

Кривая ПИАНО

Рекурсивна, в каждой части отрезка применяется

Процедура

Фрактал – это вызов подобного себе.

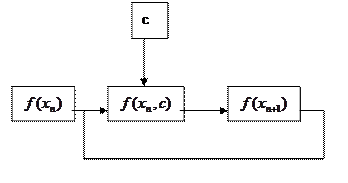
Пока с целое – ничего особенного

с вещественное – множество Монденброта

Свойства фракталов

1. Компактно и ограничено.

2. Для любой достаточно малой частицы.

3. достаточно большая часть подобна ей

Самоподобие – основное свойство фрактала

4. Фрактал – некая геометрическая фигура, состоящая из частей, каждая из которых представляет собой уменьшенную копию исходной фигуры.

5. Некая граничная линия, имеющая бесконечную длину, но вводя дробную размерность можно говорить о ее длине.

Линия не самопересекается.

Виды фракталов.

1. Геометрический

2. Алгебраический

3. Система интегрирующих функций

4. Стохастический

1) Геометрический – фрактал получаемый путем простых геометрических преобразований

Кривая Пиано, Снежинка Коха.

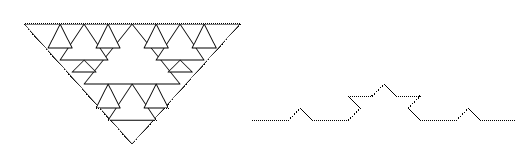
L- System (одновременно с “черепашьей графикой” – штрих рисование)

Если F – прочертить отрезок

+ - поворот по часовой стрелке

- - поворот против часовой стрелке

то кривая Коха F=F+F—F+F

2) Алгебраический – строятся на основе некоторых алгебраических формул.

Многократный итерационный процесс вызова функций с некоторой const с (веществ.

, которая плоскость)

3) Система итерирующих функций IFC Применение таких преобразований, которые дают ту фигуру которую необходимо.

Папоротник – (рекурсивная функция с применением аффинных операций)

Рекурсивная операция требует большой вычислительной мощности.

4) Стохастический

Прим. Плазма.

Если не цвет, а координата плоскость

Некоторые возмущения

Проективная геометрия

Проективная плоскость – в отличие от эвклидовой не имеет безконечной протяженности.

В этой геометрии не бывает паралельных линий.

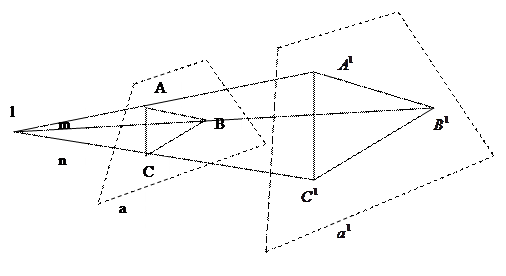
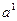- проекционная плоско

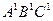- проекция ABC

m,l,n – проекционные лучи

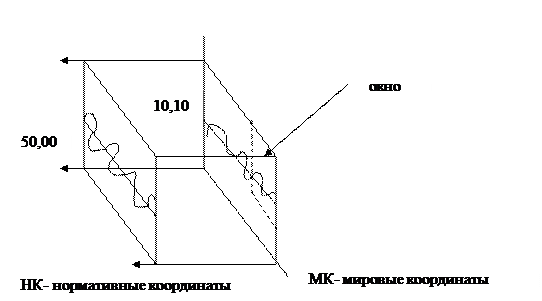
отображаем на нормализованную плоскость.

Концептуальная модель процесса 3D вывода.

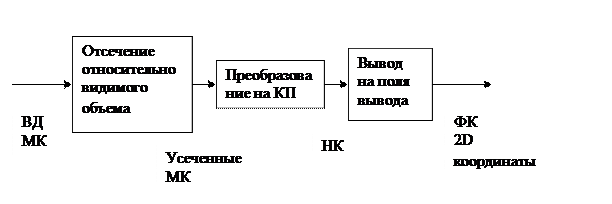
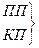точка VP viewplace с 3мя параметрами

1) Опорная точка

2) Нормаль к картинной плоскости

3) Расстояние до картинной плоскости.(КП)

Опорная (.)

Берется в МК ………………………………………………………

Расстояние до КП – расстояние от опорной (.) в направлении вектора нормали картинной плоскости.

Идеология << PHIGS, GKC,GORE >> стандарты

Опорная точка – VRP

Нормаль к картинной плоскости – VPN

Вектор направления – VHP

- Проецирование 3х мерного обьекта строится с использованием картинной плоскости и лучей проекций для получения из n – мерной проекции n-1 – ую

Причем отметим что лучи проекции проходят через каждую точку обьекта.

1) Определяется отношением между направлением проецирования и нормалью к картинной плоскости.

В ортографических проекциях эти эти соотношения совпадают, а в косоугольных наоборот.

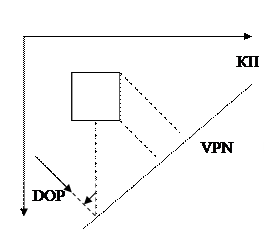
2) Ортографические проекции

Используются плоскости не перпендикулярные главным осям.

3) При аксонометрическом проецировании сохраняется паралельность лучей, углы меняются, при этом может быть измерено растояние до главных осей.

В зависимости от взаимного расположения плоскости проецирования и координатных осей различаются 3 вида аксонометрических проекций:

- Аксонометрия:

все 3 угла между координатными осями и нормалью КП равны между собой

- Димметрия

два угла между нормалью КП и координатными осями равны

- Триметрия

все углы между нормалью КП и координатными осями различны.

Все эти проекции получаются комбинацией поворотов, за которыми следует паралельное проектирование.

При повороте на угол 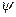относительно оси ординат потом --//---//---// 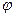---//--//--- абсцисс и последующее проецирование вдоль оси аппликат получим матрицу:

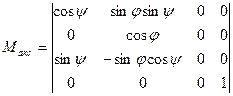
Самостоятельно построить матричную проекцию на плоскость паралельную осям

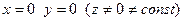
Изометрическое проецирование обладает свойством:

Расстояние по всем 3м главным осям укорачивается с одним и тем же коэффициентом, поэтому возможно с одним и тем же масштаб коэф. по всем 3м осям.

Косоугольная

Сочетает в себе свойства ортографической проекции со свойствами аксонометрии.

1) Проекционная плоскость перпендикулярна главной координатной оси сторона обьекта, паралельная этой плоскости проецирования т. о., то что может измерить углы и расстояния.

2) Проецирование других сторон позв. с помощью простейших геометрических преобразований определять расстояния и углы (линейное вычисление)

3) Нормаль КП и направление проецирования при косоугольной проекции не совпадают.

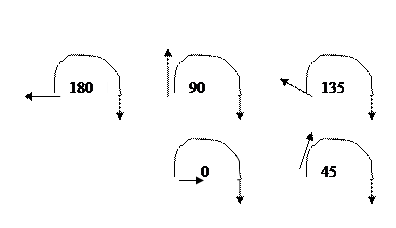
Свободное проецирование (ковалье)

Углы в направлении проецирования составляют с плоскостью 45 градусов. В результате проекции отрезка перпендикулярного проецирующей плоскости имеет ту же длинну, что и сам отрезок.

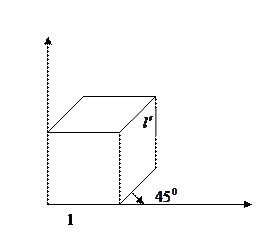
Кабинетное проектирование (кабине)

Направление проецирования с плоскостью угол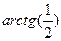

При этом соотношение отрезка перпендикулярного КП 1:2 (соотношение длинне отрезка и его проекции)

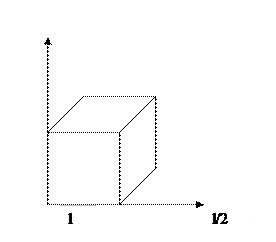
Табл. паралельное проецирование

Многовидовая ортография

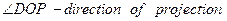
· VPN паралельна всем осям

· DOP паралельна VPN

· Видна вся грань

Аксонометрическая проекция

· VPN не паралельна осям кооординат

· DOP паралельна VPN

· Изменяется размер. Размер – функция угла между нормалью грани и DOP

Косоугольная проекция

· VPN не паралельна

· DOP не паралельна VPN

· Изменение граней за исключением паралельной КП

Центральное проецирование

	1-точеч
	2-точеч

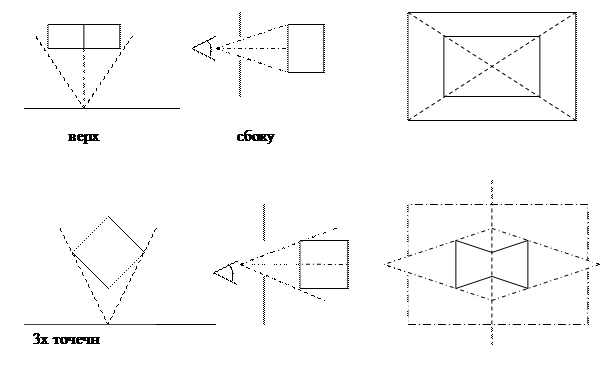
Обьект подв. центр проецир. из любой точки.

Математическое описание центральной проекции.

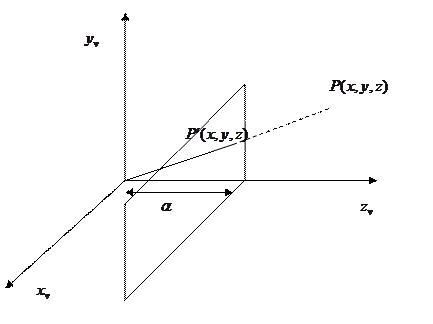
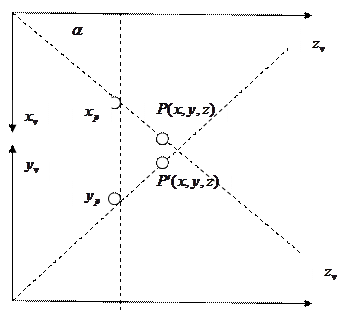
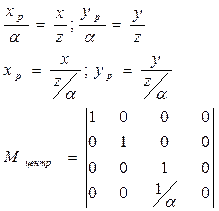
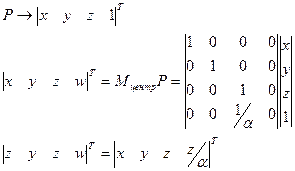
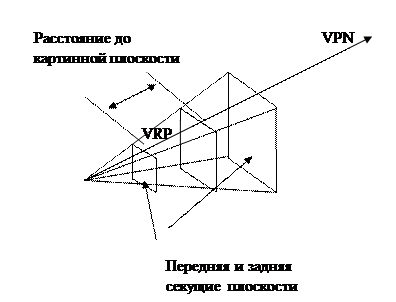Пирамида видимости

а Параллелограмм видимости

Интерполяция и аппроксимация кривых и поверхностей

В комплексной графике часто задача восполнения данных (несколько точек через через которую и провести кривую). Это и есть интерполяция, частный случай аппроксимации.

Если нужно аппроксимировать некоторую f(t), то надо искать некоторую конечную сумму.

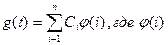не которые простые ф-ции, такие что может выполнить ограничения наложеные на g(t)

На g(t) нужно наложить n ограничений

(Хорошее приближение) f(t)

Интерполяционное ограничение

1)

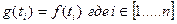
Эти 2 функции должны иметь одинаковые значения в выделеных точках.

2)Это смесь интерполяционных ограничений и ограничений гладкости

а)

б)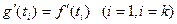

в)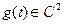

т.е. g(t) дважды дифференцируема(непрерывна)

В машинной графике нас интересует качество обьектов с которыми мы работаем (качество аппроксимации)

Свойства выражаются через внешний вид обьекта -> свойства формы.

В машинной графике невозможно записать обьект вформе у есть функция от х

Почему?

· Форма большинства обьектов не зависит от координат. Если надо восстановить кривую по нескольким точкам, которую мы изм-ем на обьект то важнейший факт, это соотношение точек не зависит от системы координат.

· Форма реальных обьектовчесто имеет вертикальныекасательные. Если Если такой обьект выражается через у от х то невозможно выявить эту поверхность аналитическим путем.

· В машинной практике мы часто имеем дело с неплоскими и незамкнутыми поверхностями которые не могут быть представлены обычными функциями.

Явная и неявная параметрическая формула

Явная формула это уравнение вида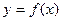

Неявная форма: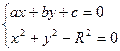

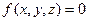уравнение описывающее поверхность

Параметрическая форма

Каждая координата точки, принадлежащая кривой представляется функцией независимой переменной t которая называется параметром этой кривой.

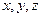запишем как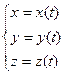

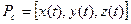матричное представление

Доводы в пользу используемых параметрич.

1. Возможность локального контроля формы
2. Гладкость и непрерывност в математическом смысле
3. возможность математического вычисления производных
4. Устойчивость к малым воздействиям (возмущениям)
5. Возможность использовать простые и значительно высокоскоростные методы закраски

Сценарий работы с кривыми

В процессе конструирования есть ->(.)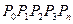

Аппроксимирование (контрольные точки)

1) Отмечаем начальные контрольные точки

2) Генерируем с помощью алгоритма

3) Коррекция кривой исправл. контрольные точки

Интерполяция в сравнении с аппроксимацией

1) Если мы интерполируем кривую то алгоритм то алгоритм интерполяции возвращает (.) вдоль кривой p(t) которая в определенный момент времени t через эти точки проходит

Промежуток между этими точками формируется в виде гладкой кривой.

2) Кривая P(t) аппроксимируется контрольными точками и осуществляется приближение кривой к этим контрольныцм точкам.

В качестве полинома нам нужно: чем выше степень полинома тем больше вычислений и наобором.

Наибольший эффект при применении кубических полиномов.

Параметрические кубические кривые – это кривые в которых x y z многочлены 3го порядка относительно t

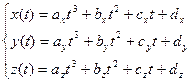
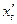
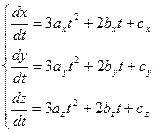
Эти уравнения задают вектор а tg угла наклона

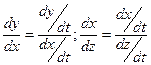
Говорим о кривой 3го порядка т.к. нет кривой более крупного порядка которая бы обеспечивала в точке сопряжения кривых друг с другом непрерывность положения и наклона.

И в тоже время обеспечивалоа прохождение кольцевых точек сегмента через заданные точки

При описании кривых можно пользоваться обозначениями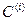

Значение i определяет свойства:

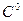- непрерывны если не имеют разрывов

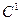- кривые непрерывны если кроме того непрерывны и их касательные.

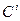- эта непрерывность обозначает что непрерывность ф-ции и ее первых производных.

1) Метод Эрмита – в котором задаются положения начальных, конечных точек кривой и вектора к ним

2) Метод Безье - задается положение конечных точек кривой, а для неявного задания касательных используются 2 другие точки не лежащие на кривой.

3) В - сплайны - для этого метода конечные точки не лежат на кривой в результате 1 и 2 производные являются непрерывными на кольцевых точках.

Кривая Эрмита

Кубическая кривая при которой определяются кольцевые точки, и определены касательные вектора этой кривой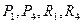

Эрмитовый вектор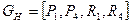

Использовать его к 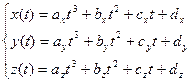ПИШЕМ ТОЛЬКО ДЛЯ X Для экономии места!

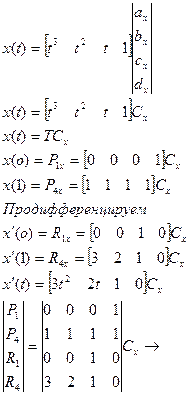
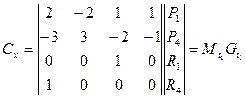
Свойства

1) 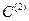- гладкая кривая

2) проходит через вершины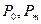

3) касательный вектор однозначно определяется через массив вершин

4) Не лежит в выпуклой оболочке порожденной матрицей образованной вершинами P

5) Аффинно – инвариантна

6) При добавлении хотя бы 1 точки вершины возникает необходимость полного пересчета всех параметрических уравнений.

7) Изменение хотя бы 1-й вершины | касательной вектора в концевых точках приводит к изменению формы кривой.

Кривая Безье.

Определяемая массивом P называется кривая определяемая следующим векторным уравнением.

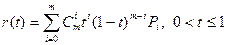
где 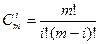коэффициэнты в различных биномах. Суть этих коэффициентов в вершинах P – универсальные многочлены Бернштейна; они > 0

Свойства

1) Гладкая кривая

2) Лежит в выпуклой оболочке

3) Ассиметрично сохраняет форму при перемене порядка вершин в массиве вершин.

4) Аффинно – инвариантна

5) Повторяет опорную ломаную

6) Если точки 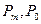лежат на одной прямой (горизонтальной| вертикальной), то то кривая совпадает с ломаной.

7) Степень функционального многочлена напрямую связана с количеством вершин (на 1 больше) и растет при его увеличении)

8) При добавлении хотя бы одной вершины возникает необходимость пересчета параметрического уравнения кривой.

9) Изменение 1й вершины приводит к заметному изменению кривой Безье.

10) Т.к. поведение кривой Безье определяется нетолько набором вершин, но и параметрическими коэфициентами, их называют весовыми коэффициентами (параметры формы)

11) Формой кривой Безье можно управлять изменяя весовые коэффициэнты| параметрические формы.

Опорная ломаная.

При m =3 получим универсальную кубическую кривую Безье (универсальные вершины (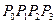) и универсальное параметрическое уравнение

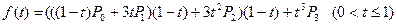
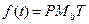
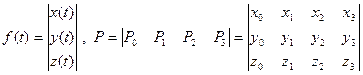
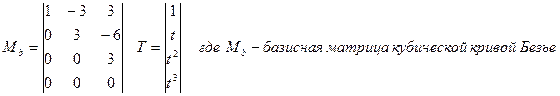
Как зависит форма кривой Безье от изменения положения точек.

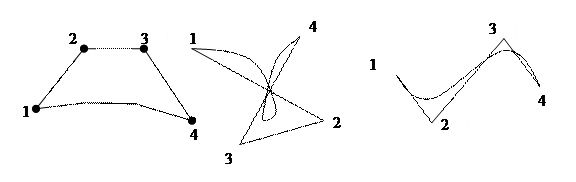
В – сплайны

1946 г.

Задаются коэффициенты сравнительно небольшего числа опорных точек лежащего на поверхности и через точки проводятся плавные поверхности.

Кривые представляются в виде кубических В – сплайнов. В общем сплайн может проходить через любое количество управляющих точек.

Обеспечивается направленность 1-й и 2-й производной в конечных точках.

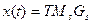
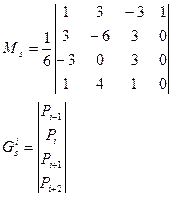
- геометрический коэффициент В – сплайна ()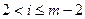

В – сплайн

Свойства кривой В-сплайна

1) 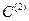- гладкой

2) не проходит ни через 1 точку массива

3) лежит в выпуклой оболочке порождаемой этим массивом

4) повторяет опорную ломаную

5) если опорные точки находятся на прямой, то В – сплайн лежит на этой прямой.

6) если опорные точки лежат в одной плоскости (компланарные), то составная (В- сплайновая) кривая лежит в этой плоскости.

7) изменение одной из вершин приводит только к изменению части кривой

8) При добавлении 1 вершины возникает необходимость пересчета 1-х элементов кривых (параметрическое уравнение)

9) аффинно инвариантна

10) проективно инвариантна (проективные преобразования не влияют на форму нашей кривой)

11) существуют весовые коэффициенты

Д\З кубические поверхности.

Алгоритмы растровой графики

Генерация линий

1) Генерируемый отрезок должен быть прямым

2) Начинаться и заканчиваться в заданных точках.

3) Яркость отрезка по всей длинне должна быть одинаковая и не зависеть от угла и наклона

4) Алгоритм рисования линий должен быть быстрым

Все 4 условия одновременно не могут быть соблюдены

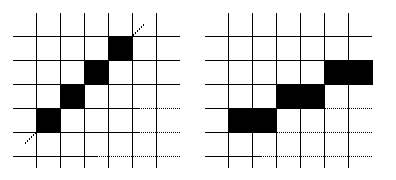
Алгоритмы для генерации линий.

1) Находят приближенную длинну отрезка.

2) Стараются свести вычисляемые операции к минимуму. Стараются прийти к целостным данным.

3) Перевести реализацию этих алгоритмов.на аппаратный уровень.

Простой пошаговый алгоритм.

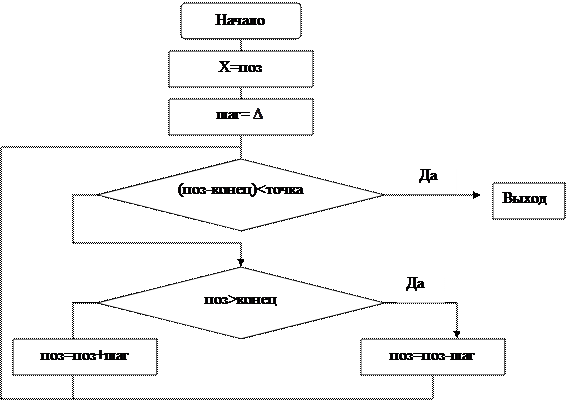
Цифровой дифференциальный анализатор.

Разложение отрезка в растр (генерация отрезка)состоит в решении ДУ.

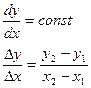
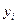- начальное значение для очередного шага вдоль отрезка.

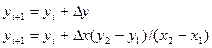
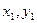- концы отрезка

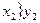
Процедура разложения в растр по методу ЦДА

1) Предполагается, что концы отрезков не совпадают

2) Апроксимируем длинну отрезка.

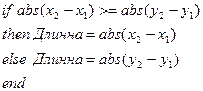
3) Полагаем большее из приращений

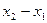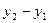или =1

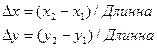
Округляем величины но не отбрасываемдробную часть.

Воспользуемся функцией sign:

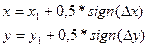
4) Начало основного цикла

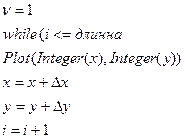
end

Метод деления отрезка пополам.

Делят пополам

Алгоритм Безенхейма.

зависят от углового коэффициэнта изменяется на единицу (в зависимости от коэфициэнта)

Координата другой зависит от расстояния между действующим положением отрезка и ближней координатой сетки.

Растровая развертка в реальном времени

2 типа информации:

1) Виртуальные атрибуты (свет, цвет, оттенок)

2) геометрические атрибуты (координаты х,у, текстовая информация)

Информация будет упорядочена.

Вычисляется интенсивность вывода на экран.

Сложность в том: скорость вывода на экран.

Простейший алгоритм построчного сканирования.

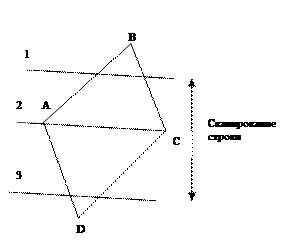
BC	BC	BC
BA	BA	BA
BD	BD	BD
CD	CD	CD
AD	AB	AD

BA	BA	BA
BC	BC	BC
BD	BD	BD
CD	CD	CD
AD	AD	AD

2 формы сортировки

Порядок сортировки начинаемый с у влияет на размер списка активных ребер.

Либо обрабатывается больше информации чем нужно для данной строки.

Развертка с групповой сортировкой.

Проблема борьбы с избыточной информацией решается за счет введения дополнительных данных.

Вначале выполняется групповая сортировка по у всех отрезков изображения.

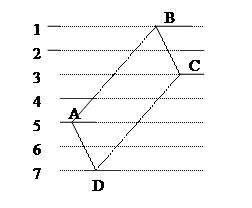
У – группа

1- пусто

2 -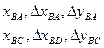

3 – пусто

4 -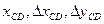

5 – пусто

6 -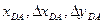

7 – пусто

8 – пусто

При групповой сортировке по у образуются области памяти или группы.

При просмотре дисплейного списка заносится информация в группу, соответствующей наибольшей у координате.

х –координата точки пересечения со сканирующей строкой.

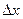- изменение координаты х при переходе одной с другой

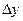- число сканирующих строк пересекаемых данным отрезком.

Алгоритм

1) Список активных ребер для каждой сканирующей строки формируется добавлением информации из каждой у группы соответствующей сканирующей строке.

2) Координаты х точек пересечения

сортируется в порядке сканирования, а ребра из списка активных ребер преобразуются в растровую форму.

3) Для каждого отрезка список активных ребер 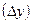число пересечения со сканирующей строкой уменьшается на единицу. Если 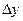отрицательный то отрезок исключается из списка.

4) Для каждого отрезка координата х получается добавлением

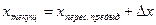
список активных ребер

сканирование строки 3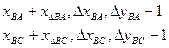

сканирование строки 5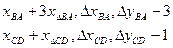

сканирование строки 7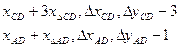

тип гранично определенный

4-рех или 8-ми связные пикселы

4-х связный связан в 4-х направлениях

8-ми связный соответственно в 8-ми

(используются реже – сложный алгоритм многопроходный)

Простой рекурсивный алгоритм закрашивания по затравке

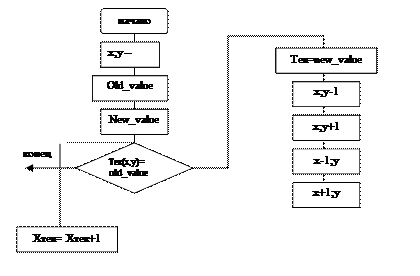
О ступенчатости: (classing)

Если есть: ступенчатость

Отсечение

В глобальном смысле в широком спектре задач применяется алгоритм отсечения.

Процесс отсечения – это выделение определенной базы данных. Применяются в алгоритмах удаления невидимых поверхностей, в методах построения теней, в методах

Построения текстуры (фактуры). Выделяется 2-х мерное отсечение и 3-х мерное.

Алгогритмы могут реализовываться как програмным так и аппаратным способом.

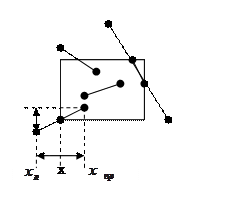
2-х мерное отсечение.

Определить отрезки попадающие

внутрь прямоугольника

Отсечение

Способы выбора простоты решений => 2 вида

1) Алгоритмы использующие (группы алгоритм. Отсечения) кодирование концов отрезка или всего отрезка.

2) Алгоритм использует параметрическое описание отрезка и самого ока отсечения.

1. Алгоритм деления отрезка пополам CS Койна – Сазерленда; FS –алгоритмы(fast clipping)
2. Алгоритм Кирус-Бека.

Алгоритм Коэна – Сазерленда.

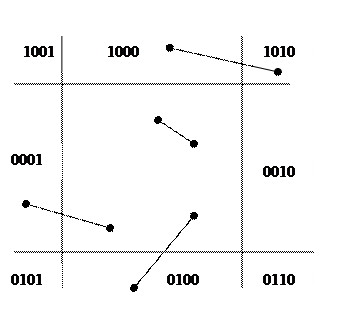
Эффективен если есть отрезки внутри

и вне и мало отрезков на пересечении

Делится на 8 областей, каждая кодируется 4-х разрядным кодом.

Внутренняя область: 0000

1-ца в разряде говорит о том к какой области принадлежит отрезок

1-ца в первом разряде => над окном

1-ца во втором разряде => под окном

1-ца в третьем разряде => над правее

Шаги определяются нахождением положительных отрезков.

1) Сами коды обоих концевыцх точек отрезка => отрезок в окне

2) Если логическое И кодов обоих концевых отрезков не = 0 => отрезок целиком вне окна

3) Если логическое И кодов обоих концов = 0 => этот подоз- ный отрезок может быть частично видим или целиком невидим т.е. на границе => определяются точки пересечения с окном.

FC – алгоритм.

Делится на 5 областей.

Кодировка самого отрезка 16 – ричным кодом, а не как в предыдущем алгоритме концевых точек.

Алгоритм работает по определенной принадлежности отрезка к областям.

Дата добавления: 2014-11-28