Лабораторная работа №6

Информационный анализ зависимых сообщений.

1. Краткие теоретические сведения. При решении задач информационного анализа часто приходится исследовать несколько источников, дающих зависимые сообщения. Совокупность сообщений, вырабатываемых несколькими источниками, называется сложным сообщением.

Пусть имеется два источника сообщений. События первого источника принимают значения х₁, х₂,..., х_n с вероятностями р(х₁), р(х₂),..., р(х_n), а второго- y₁, y₂,..., y_m с вероятностями р(y₁),р(y₂),..., р(y_m). Совместная энтропия такого сложного сообщения определяется по формуле:

(1)

p(x_i,y_i)-вероятность совместного появления сообщений x_i и y_i. Для сложных сообщений имеют место соотношения:

(2)

-энтропия сообщения х; (3)

-энтропия сообщения у; (4)

-средняя условная энтропия сообщения y(энтропия y при условии, что сообщение x уже поступило);(5)

-средняя условная энтропия сообщения x (энтропия x при условии, что сообщение y уже поступило); (6)

На практике при информационном анализе сложных сообщений вероятности p(x), p(y), p(x/y), p(y/x) приближенно оцениваются относительными частотами, которые вычисляются на основе экспериментальных данных.

2. Постановка задачи. Для оценки состояния объекта используются два статистически зависимых параметра X и Y.В результате эксперимента получены реализации процессов X(t), Y(t) на интервале 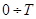. Требуется выполнить информационный анализ сложного сообщения (X,Y) о состоянии объекта.

3. Методика решения задачи.

3.1. Реализации непрерывных процессов X(t), Y(t) представляются в виде дискретных отсчетов X_k, Y_k (N- общее количество точек реализации). Диапазоны изменения X и Y разбиваются на n и m интервалов в зависимости от необходимой точности измерения и .

3.2. Определяются относительные частоты попадания X и Y в интервалы W(x_i), W(y_i), а также относительные частоты событий W(x_i,y_i). Составляется таблица:

Yi	Xi	W(yj)
	X1	x2	…	xn
y1	W(x1, y1)	W(x2, y1)	…	W(xn, y1)	W(y1)
y2	W(x1, y2)	W(x2, y2)	…	W(xn, y2)	W(y2)
…	…	…	…	…	…
ym	W(x1, ym)	W(x2, ym)	…	W(xn, ym)	W(ym)
W(xi)	W(x1)	W(x2)	…	W(xn)

3.3. Оценивается энтропия сообщений H(x), H(Y), по формулам:

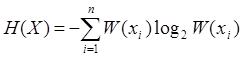
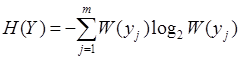
3.4. Определяется энтропия сложного сообщения:

3.5. Рассчитывается условная энтропия по формулам:

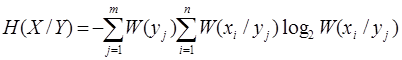
3.6. Выполняется проверка расчетов с использованием соотношения:

4. Пример. Исходные данные. Даны две реализации процессов изменения статистически зависимых параметров X(t), Y(t).Требуется выполнить информационный анализ сложного сообщения (X,Y). Шаг квантования по времени . Необходимая точность измерения параметров .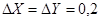

1.Непрерывные реализации X(t), Y(t) на интервале 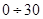c представляем в виде дискретных отсчетов X_k, Y_k 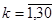, т.к.

Таблица1

T
X		0.4	0.7		1.2	2.7	3.6	3.4	4.2	4.8	5.8	5.6	5.4	5.3	6.2
Y	0.6		1.5			2.8	2.7	3.2	3.8		6.4		7.4		6.6

T
X	6.9	7.8	8.7	9.1	9.8	9.6	9.9		8.4	7.7	7.6	6.7	5.4	5.5
Y	7.4		7.6	8.3	8.6	9.4	9.3		9.5	9.5	9.4	8.4	7.5		8.5

Диапазон изменения X и Y разбиваем на 5 интервалов, т.к. 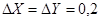. Интервалы:(0;0.2) (0.2;0.4) (0.4;0.6) (0.6;0.8) (0.8;1).

2. Определяем по таблице 1 относительные частоты попадания X и Y в интервалы W(x_i); W(y_i), а также относительные частоты событий (x_i, y_i):W(x_i, y_i). Данные сводим в таблицу №2.

Таблица 2

	Xi
Yi	x1	x2	x3	x4	x5	W(yj)
y1	3/30					3/30
y2	2/30	3/30	1/30			6/30
y3			1/30			1/30
y4			7/30	3/30	1/30	11/30
y5				3/30	6/30	9/30
W(xi)	5/30	3/30	9/30	6/30	7/30

3. Оцениваем энтропию сообщений H(X),H(Y):

4. Определяем энтропию сложного сообщения H(x, y):

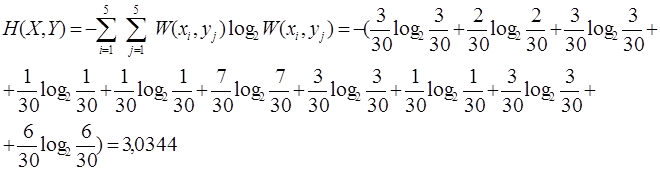
5. Вычисляем условные энтропии:

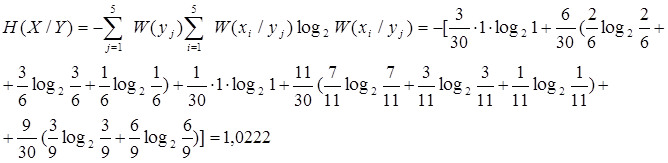
6. Выполняем проверку:

Точность расчетов удовлетворительная.

5. Задание. Для заданных реализаций X(t), Y(t) статистически зависимых величин выполнить информационный анализ сложного сообщения (X, Y).

Расчет информационных цепей.

Теоретические сведения. Информационная цепь представляет собой совокупность взаимодействующих источников, преобразователей и потребителей информации. Информационные цепи могут рассматриваться как модели процессов в системах управления различной природы. В общем случае информационные цепи представляют собой довольно сложные сильно разветвленные структуры. В простейшем случае система управления может быть представлена информационной цепью, содержащей источник, приемник и два информационных канала (рис. 1).

При этом управляющее устройство выступает в роли источника управляющей информации, а управляемый объект - в роли приемника или информационной нагрузки. Формализация информационных цепей может быть выполнена с использованием типовых идеализированных элементов по аналогии с электрическими, механическими, пневматическими цепями.

Информационное напряжение источника равно разности энтропий объекта управления (или логарифму отношения вероятностей) без управления Н₀ и при наличии управления Н₁, т.е.

(1)

Информационное сопротивление приемника равно времени реакции объекта управления на управляющую информацию r_Н (с).

Информационный ток через активную нагрузку равен отношению:

(бит/с) (2)

Источник информации также характеризуется сопротивлением r_вн, которое определяется временем принятия решения. Кроме внутреннего сопротивления r_вн источник характеризуется величиной информационно- движущей логики ИДЛ h, равной информационному напряжению на холостом ходу. ИДЛ характеризует интеллектуальные возможности источника при неограниченном времени на принятие решений. Т.о. простейшая полная информационная цепь имеет следующую структуру (рис. 2).

Для этой схемы информационный ток равен:

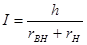
Кроме того:

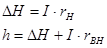
В общем случае нагрузка характеризуется кроме информационного сопротивления также памятью и ригидностью.

Память определяется емкостью n, которая равна отношению запомненной информации 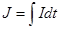к eе потенциалу (напряжению) 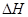, т. е.

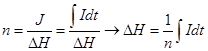(3)

Ригидностью называется свойство нагрузки, выражающееся в активном противодействии управлению, т. е. в выработке нагрузкой встречного информационного напряжения:

(4)

L - ригидность (с²).

С учетом свойств памяти и ригидности информационные цепи могут более сложную структуру. Для расчета таких цепей используются универсальные формулы, выражарающие законы Кирхгофа для информационных цепей.

1. Для любого узла информационной цепи алгебраическая сумма токов равна нулю:

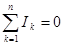(5)

2. Сумма падений напряжений вдоль любого замкнутого контура информационной цепи равна нулю:

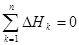(6)

По известным токам и напряжениям можно рассчитать информационную мощность:

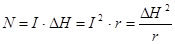(7)

Информационная мощность трактуется как рассеиваемый (на нагрузке) или вырабатываемый (источником) в единицу времени смысл С соответвующей интеллектуальной деятельности:

(8)

Если информационная цепь содержит источники и только активные элементы r, то выражение (5), (6) представляют собой систему алгебраических уравнений.

Пример 1. Информационная цепь задана структурной схемой (рис. 3). Требуется рассчитать информационные токи в цепи, а также смысл С₄, рассеянный на элементе r₄ за два часа работы системы, если h=10 бит; r_вн=0.5 с; r₁=1 c; r₂=r₃=5 c; r₄=2 c.

Используя соотношения (5) и (6) составим 5 алгебраических уравнений для определения информационных токов I₁, I₂, I₃, I₄, I₅:

I₅=I₁+I₂ - для узла А

I₂=I₃+I₄ - для узла Е

h=I₅r_BH+I₁r₁ - для контура ABC

h=I₂r₂+I₃r₃ - для контура AEDC

I₃r₃=I₄r₄ - для контура DEF

Подставляя значения параметров, получим:

Решая систему, найдем: I₁=2,963 бит/с; I₂=11,111 бит/с; I₃=8,889 бит/с; I₄=2,222 бит/с; I₅=14,074 бит/с.

Мощность, рассеиваемая на элементе r₄, равна:

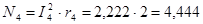бит/с

С учетом того, что n₄ не зависит от времени, определим смысл, рассеянный на r₄ за два часа работы:

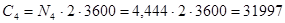бит²

Если информационная цепь содержит запоминающие и ригидные элементы, то выражения (5), (6) представляют собой систему дифференциальных уравнений, которая описывает переходные процессы в цепи для заданных значений параметров и начальных условий. При этом токи, напряжения и мощности будут представлять собой функции времени.

Пример 2. Информационная цепь задана структурной схемой (рис. 4). Для заданных значений параметров и начальных условий требуется определить закон изменения информационного тока на элементе r₂, а также смысл, рассеянный на этом элементе за интервал времени c.

r_BH=1 c; r₁=0,6 c; r₂=2 c; n=2; L=0,5 c²; h=1 бит; .

В соответствии с соотношениями (5), (6), составим систему дифференциальных и алгебраических уравнений для определения информационных токов в цепи:

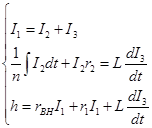
- для узла С

- для контура DCE

- для контура ABCE

Введем обозначение r_BH+r₁=2. Тогда с учетом I₁=I₂+I₃, третье уравнение системы примет вид:

Второе уравнение перепишем так:

Имеем систему:

Поставим в выражения для 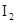и во второе уравнение системы и приведем подобные:

С учетом известных исходных данных:

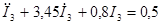
Решение уравнения ищется в виде суммы:

где I”₃ - решение алгебраического уравнения.

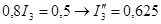
I’₃ есть решение исходного дифференциального уравнения без правой части:

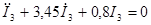
Т. к. корни характеристического уравнения

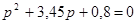
действительные р₁=-0,25; р₂=-3,2, то решение для I’₃ есть сумма экспонент:

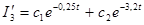
Значит, общее решение имеет вид:

Постоянные с₁ и с₂ найдем с учетом начальных условий :

Частное решение для I₃ имеет вид:

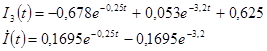
Закон изменения информационного тока I₂:

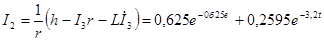
Процесс изменения информационной мощности на сопротивлении r₂:

Смысл, рассеянный на элементе r₂ за интервал времени c равен:

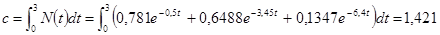бит

Задание. Для заданной информационной цепи рассчитать информационные токи, мощность и смысл, рассеиваемые на выделенном элементе.

Дата добавления: 2014-11-29