
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади квадровних фігур
|
|
|
|
Теорема 1.5. Якщо плоска фігура  має внутрішню точку, то внутрішня площа цієї фігури додатна (
має внутрішню точку, то внутрішня площа цієї фігури додатна (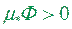 ), у протилежному випадку -
), у протилежному випадку - 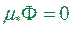 .
.
 Доведення. 1) Нехай фігура
Доведення. 1) Нехай фігура 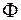 має внутрішню точку
має внутрішню точку 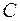 , тобто існує відкритий круг
, тобто існує відкритий круг 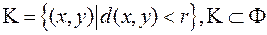 . У цьому крузі радіуса
. У цьому крузі радіуса  розглянемо квадрат
розглянемо квадрат 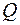 рангу
рангу 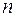 , який місить точку
, який місить точку 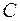 , і такий, що довжина його діагоналі менша від радіуса:
, і такий, що довжина його діагоналі менша від радіуса: 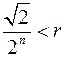 .
.
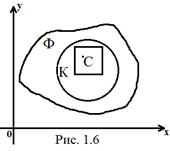
Отже, кожна точка квадрата відділена від точки 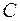 на відстань, меншу його діагоналі, а значить і радіус круга. Тому
на відстань, меншу його діагоналі, а значить і радіус круга. Тому 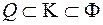 (рис. 1.6), звідки
(рис. 1.6), звідки 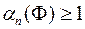 , тому
, тому 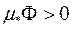 .
.
2) Нехай фігура 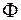 не має жодної внутрішньої точки, тому
не має жодної внутрішньої точки, тому 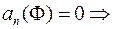
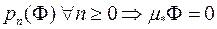 . ■
. ■
Приклад 1. Кожний прямокутник 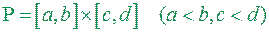 квадровний і
квадровний і 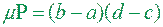 µ P=(b-a)(d-c).
µ P=(b-a)(d-c).
 Доведення. Квадрат
Доведення. Квадрат 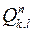 рангу
рангу 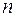 буде міститися у прямокутнику
буде міститися у прямокутнику 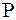 , якщо
, якщо
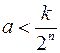 ,
, 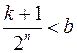 ,
, 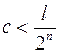 ,
, 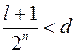 , звідки
, звідки 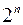
 .
.
Останні нерівності будуть виконуватись, якщо
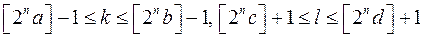
(тут ми використали правильну для будь-яких 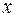 нерівність
нерівність
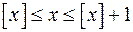 ), або
), або
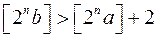 і
і 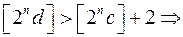 (1.12)
(1.12)
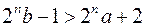 і
і 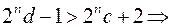
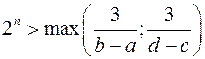 (1.13)
(1.13)
Оскільки 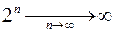 , то завжди можна підібрати достатньо великий номер
, то завжди можна підібрати достатньо великий номер 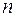 , при якому нерівність (1.13) виконується. Якщо першій нерівності (1.12) відповідає
, при якому нерівність (1.13) виконується. Якщо першій нерівності (1.12) відповідає 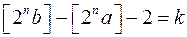 значень, а другій
значень, а другій 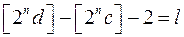 , то всіх квадратів
, то всіх квадратів  буде
буде 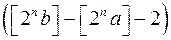
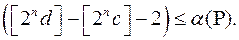
Поділимо на 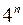 :
:
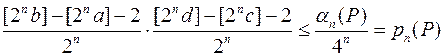 . (1.14)
. (1.14)
Перш, ніж продовжувати наші міркування, розглянемо очевидну нерівність 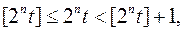
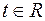 . Розділимо всі частини на
. Розділимо всі частини на 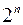 :
:
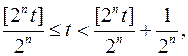
і перейдемо до границі при 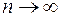 :
:
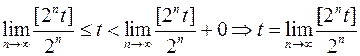 .
.
Отже, в нерівності (1.14) перейдемо до границі при 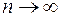
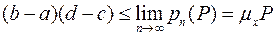 (1.15)
(1.15)
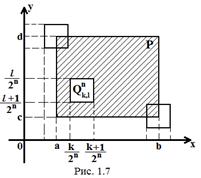
з іншого боку, квадрат 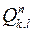 буде перетинатися з
буде перетинатися з 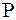 (тобто мати з
(тобто мати з 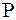 принаймні одну спільну точку), якщо проекції на координатні осі квадрата
принаймні одну спільну точку), якщо проекції на координатні осі квадрата 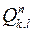 і прямокутника
і прямокутника 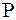 перетинаються, тобто (рис. 1.17)
перетинаються, тобто (рис. 1.17)
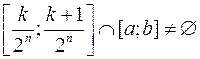 і
і 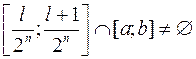 .
.
При цьому
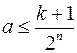 ,
, 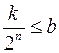 i
i 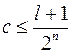 ,
, 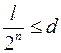 ,
,
або 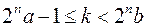 і
і 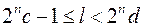 ,
,
звідки 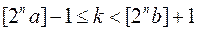 і
і 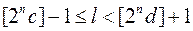 (1.15)
(1.15)
Значить квадратів 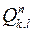 , які задовольняють умови (1.15), є
, які задовольняють умови (1.15), є 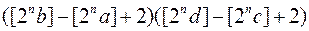 , і кожний квадрат, який має принаймні одну спільну точку з прямокутником
, і кожний квадрат, який має принаймні одну спільну точку з прямокутником 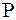 , знаходиться серед них, то
, знаходиться серед них, то
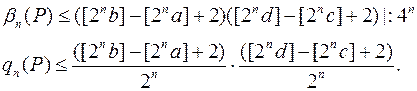
В останній нерівності перейдемо до границі при 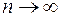 :
:
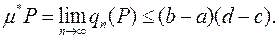 (1.16)
(1.16)
Співставляючи нерівності (1.15) і (1.16) бачимо, що
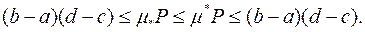
Отже, прямокутник 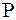 є квадровною фігурою і його площа
є квадровною фігурою і його площа 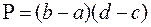 . ■
. ■
 Приклад 2. Кожна ламана
Приклад 2. Кожна ламана 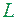 на площині з скінченним числом відрізків квадровна і має площу, рівну нулю.
на площині з скінченним числом відрізків квадровна і має площу, рівну нулю.
Для доведення розглянемо ламану, яка складається з одного відрізка. Оскільки відрізок не має внутрішніх точок, то за теоремо 1.5 внутрішня міра 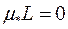 . Залишається показати, що і зовнішня міра тут дорівнює нулю.
. Залишається показати, що і зовнішня міра тут дорівнює нулю.
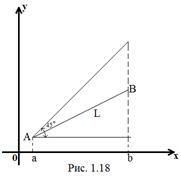
Відрізок 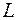 нахилений до однієї з координатних осей на кут, не більший
нахилений до однієї з координатних осей на кут, не більший 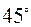 , наприклад до осі
, наприклад до осі 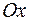 і
і 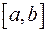 – його проекція на
– його проекція на 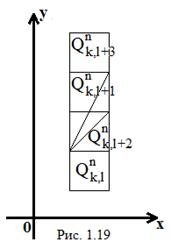 цю вісь (рис 1.18). Оскільки
цю вісь (рис 1.18). Оскільки
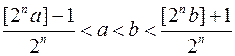 ,
,
то кожний квадрат рангу 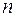 , який має з
, який має з 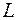 принаймні одну спільну точку, проектується у відрізок
принаймні одну спільну точку, проектується у відрізок 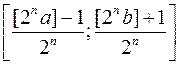 осі
осі 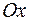 і число такий проекцій не перевищує
і число такий проекцій не перевищує 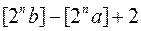 . При цьому квадратів з однією і тією ж проекцією не може бути більше трьох, бо якби відрізок перетинав, наприклад, квадрати
. При цьому квадратів з однією і тією ж проекцією не може бути більше трьох, бо якби відрізок перетинав, наприклад, квадрати 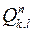 ,
, 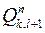 ,
, 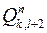 і
і 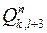 (рис. 1.19), то кут його нахилу до осі
(рис. 1.19), то кут його нахилу до осі 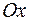 був би більший 45о. тому число β n (L) квадратів рангу
був би більший 45о. тому число β n (L) квадратів рангу 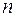 , які мають з
, які мають з 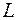 принаймні одну спільну точку, не перевищує числа
принаймні одну спільну точку, не перевищує числа 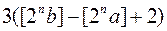 , звідки
, звідки
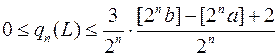 .
.
Перейдемо до границі при 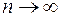 :
:
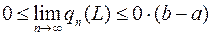 , або
, або 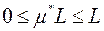 .
.
Отже 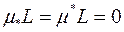 , тому відрізок є квадровна фігура, площа якої дорівнює нулю. ■
, тому відрізок є квадровна фігура, площа якої дорівнює нулю. ■
Приклад 3. Кожний трикутник, многокутник 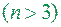 є квадровними фігурами.
є квадровними фігурами.
 Доведення. Оскільки довільний многокутник можна подати як скінченне об’єднання тиркутників, то доведення квадровності проведемо для трикутника
Доведення. Оскільки довільний многокутник можна подати як скінченне об’єднання тиркутників, то доведення квадровності проведемо для трикутника 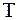 . Різниця
. Різниця
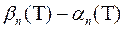
означає число квадратів 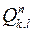 рангу
рангу 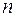 , які мають принаймні одну спільну точку з
, які мають принаймні одну спільну точку з 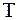 , але не належать внутрішності
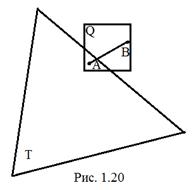
, але не належать внутрішності 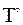 цього трикутника (рис. 1.20). Кожний такий квадрат перетинається з межею
цього трикутника (рис. 1.20). Кожний такий квадрат перетинається з межею 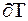 (тобто периметром) трикутника. Дійсно, візьмемо точку
(тобто периметром) трикутника. Дійсно, візьмемо точку 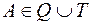 і
і 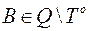 .
.
Якщо 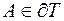 або
або 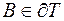 , то
, то 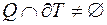 ,
,
Якщо 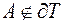 або
або 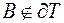 , то
, то 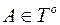 , а
, а 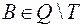 . Тоді відрізок
. Тоді відрізок 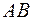 перетинатиме
перетинатиме 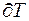 і
і 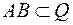 . Отже,
. Отже, 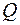 перетинається з
перетинається з 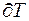 , тому
, тому
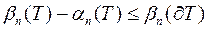 ,
,
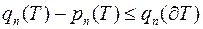 .
.
Але периметр трикутників складається з трьох відрізків, тому він квадровний і 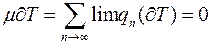 . Отже,
. Отже, 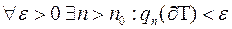 , або
, або 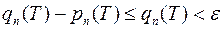 .
.
Отже, згідно з 1.1 трикутник 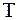 , є квадровною фігурою. ■
, є квадровною фігурою. ■
Приклад 4. Якщо 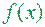 і
і 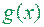 – інтегровані функції на відрізку
– інтегровані функції на відрізку 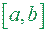 , при чому
, при чому 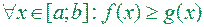 . Тоді фігура
. Тоді фігура  , обмежена графіком функцій
, обмежена графіком функцій 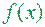 ,
, 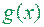 і прямим
і прямим 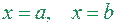 , квадровна і її площа дорівнює
, квадровна і її площа дорівнює
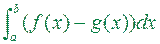 .
.
Приклад 5. Якщо функція 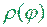 інтегровна на відрізку
інтегровна на відрізку 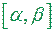 , то криволінійний сектор
, то криволінійний сектор  , який визначається цією функцією, є квадровною фігурою, площа якої дорівнює
, який визначається цією функцією, є квадровною фігурою, площа якої дорівнює
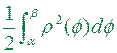 .
.
Доведення цих фактів нами проводилося при вивчені визначеного інтеграла. Нагадайте їх.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!