Кубовні тіла

Написати твір на тему «Кубовні тіла».

Програма дій.

1. Дайте означення внутрішнього і зовнішнього об’єму тіла кубовного тіла.

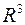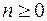Простір площинами , , () для кожного цілого розбивається на рівні куби рангу n:

.

Тілом називають довільну обмежену множину точок простору .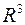

Для тіла ввести позначення , , , :

, ,

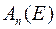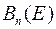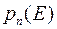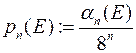і довести твердження:

1) (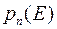) – зростаюча послідовність невід’ємних чисел,

() – спадна, при чому ;

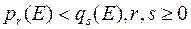2) 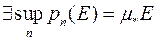, яку існують внутрішнім об’ємом тіла ;

3) 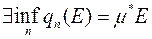, яку називають зовнішнім об’ємом тіла E;

4) .

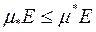Якщо 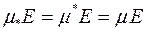, то множину називають кубовним тілом, а число - об’ємом цього тіла.

2. Основні властивості кубовних тіл.

Теорія кубовних тіл будується аналогічно теорії квадровних фігур. Зокрема треба довести наступні твердження.

1) Монотонність і адетивність об’єму;

2) Кубовність прямокутного паралелепіпеда 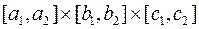і .

3) Тіло кубовне тоді і тільки тоді, коли кубовні тіла 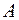і 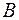такі, що 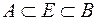і .

4) Тіло кубовне тоді і тільки тоді, коли його межа кубвна і має нульовий об’єм.

5) Всяка плоска фігура 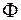в просторі 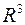кубовна і має нульовий об’єм.

6) Зв’язок між площами і об’ємами.

Нехай 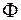– довільна фігура в площині і 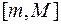- довільний відрізок на осі .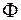

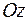Означення. Циліндричним тілом називають множину точок простору (рис. 1.22)

.

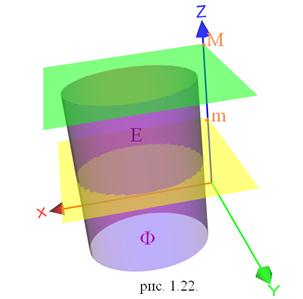Теорема. Якщо Фігура квадровна, то циліндричне тіло 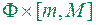кубовне і .

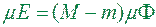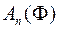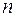Доведення. Похначемо через і квадрати рангу , які які відповідно містяться і мають принаймні одну спільну точку з 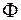, я через 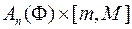і циліндричні тіла, які складаються із скінченного числа прямокутних паралелепіпедів таких, що

.

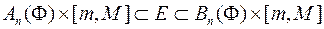Ці тіла є кубовними,а їх об’єми

,

.

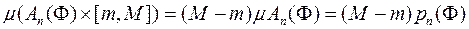Оскільки фігура 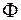квадровна, то 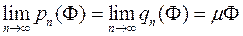і

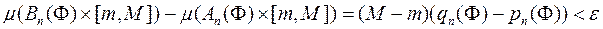
Для деякого 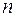. Отже, тіло кубовне і 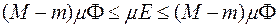, звідки і випливає потрібна рівність. ■

3. Рисунки до побудованої теорії виконайте в графічному редакторі.

Дата добавления: 2014-11-29