
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Означення подвійного інтеграла по довільній області
|
|
|
|
На минулій лекції ми означили подвійний інтеграл по прямокутнику, щоб показати аналогію з визначеним інтегралом, а також побудувати фрагмент теорії подвійних інтегралів, визначених та прямокутнику. В даній лекції ми узагальнимо поняття подвійного інтеграла на випадок довільної квадратної області.
Нехай функцію 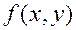 визначена на плоскій квадратній області
визначена на плоскій квадратній області 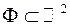 .
.
Означення 3.1. Скінченну систему  квадратних множин
квадратних множин  на площині
на площині 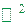 називають
називають  -розбиттям множин
-розбиттям множин  , якщо:
, якщо:
1)  ,
,  ;
;
2) Множини  не мають спільних внутрішніх точок:
не мають спільних внутрішніх точок:  ,
, 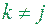 ,
,  ;
;
3) 
Розглянемо довільне 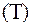 - розбиття множини
- розбиття множини 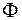 . У кожній множині
. У кожній множині  візьмемо довільну точку
візьмемо довільну точку 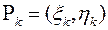 і складемо суму
і складемо суму
`  (3.1)
(3.1)
Означення 3.2. Сума вигляду (3.1) називається інтегральною сумою функції  , що відповідає даному розбиттю області
, що відповідає даному розбиттю області  на частинній області
на частинній області  ,
,  і даному вибору проміжних точок
і даному вибору проміжних точок 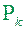 в частинних областях.
в частинних областях.
Діаметром області  називається число
називається число  , а найбільше з чисел
, а найбільше з чисел 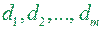 ,
,  .
.
називають діаметром  - розбиття і позначають
- розбиття і позначають
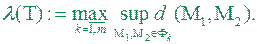
Означення 3.3 Число  називають границею інтегральної суми (3.1) при
називають границею інтегральної суми (3.1) при  , якщо для довільного додатного числа
, якщо для довільного додатного числа  можна вказати таке додатнє число
можна вказати таке додатнє число  , що при
, що при 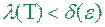 незалежно від вибору точок
незалежно від вибору точок 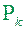 в частинних областях
в частинних областях  виконується нерівність
виконується нерівність
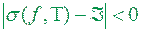 .
.
Якщо така границя  існує, то її називають подвійним інтегралом від функції
існує, то її називають подвійним інтегралом від функції  по області
по області  і позначають
і позначають
 або
або 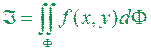 (3.2)
(3.2)
а функцію  називають інтегрованою на множину
називають інтегрованою на множину  .
.
Отже,

Теорема 3.1. (необхідна умова інтегрованості)
Якщо 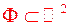 і
і 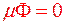 , то для довільної функції
, то для довільної функції 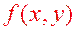 , визначеної на множині
, визначеної на множині  , подвійний інтеграл дорівнює нулю.
, подвійний інтеграл дорівнює нулю.
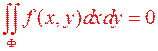
Доведення: Оскільки  , то для довільного
, то для довільного 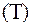 - розбиття множини
- розбиття множини 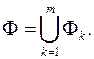 маємо, що
маємо, що  ,
, 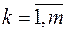 .
.
Отже,  ■
■
З теореми 3.1, зокрема випливає, що інтегрована функція  на квадратній множині міри нуль не обов’язково має бути обмеженою.
на квадратній множині міри нуль не обов’язково має бути обмеженою.
Розглянемо тепер випадок квадрової множини 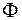 , яка задовольняє додатковій умові.
, яка задовольняє додатковій умові.
Умова 1. Для квадровної множини 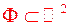 і для довільного
і для довільного 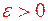 існує
існує  - розбиття множини
- розбиття множини 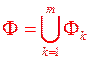 таке, що
таке, що  , а
, а 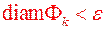 ,
, 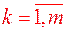 .
.
Теорема 3.2 Якщо функція виду 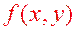 інтегрована на квадровій множині
інтегрована на квадровій множині 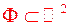 , і для множини
, і для множини  виконується умова 1, то функція
виконується умова 1, то функція  обмежена на цій множині.
обмежена на цій множині.
Доведення теореми проведемо методом від супротивного. Припустимо, функція 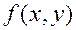 , яка задовольняє умови теореми 3.2, необмежена на множині
, яка задовольняє умови теореми 3.2, необмежена на множині 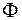 .
.
Розглянемо довільне 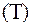 - розбиття множини
- розбиття множини 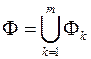 таке, що
таке, що  , а
, а 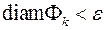 ,
, 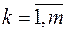 . Оскільки на множині
. Оскільки на множині 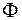 функція
функція 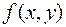 необмежена, то вона необмежена принаймі на одній на одній з множин
необмежена, то вона необмежена принаймі на одній на одній з множин  . Це означає, що на
. Це означає, що на 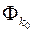 існує точка
існує точка 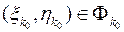 , в якій значення функції більше від довільного наперед заданого числа, зокрема
, в якій значення функції більше від довільного наперед заданого числа, зокрема
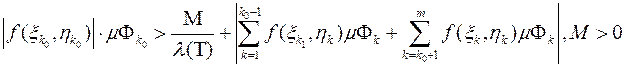 .
.
Тепер оцінимо інтегральну суму:

Отже, інтегральна сума 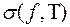 не прямує до скінченної границі при
не прямує до скінченної границі при  , а це суперечить нашому припущенню про те, необмежена функція
, а це суперечить нашому припущенню про те, необмежена функція  інтегровна на множині
інтегровна на множині  з умовою 1. ▄
з умовою 1. ▄
Аналогічно, як і в попередній лекції для обмеженої функції  , визначеної на квадровній області
, визначеної на квадровній області 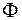 , вводять нижню та верхню суми Дарбу по заданому
, вводять нижню та верхню суми Дарбу по заданому 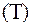 - розбиттю області
- розбиттю області 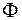 :
:
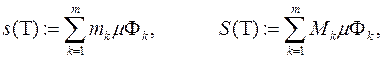
де 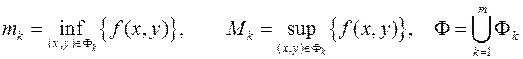
Ці суми мають властивості 1-3, сформулюванні у попередній лекції (Доведіть їх!), зокрема у властивості 3 випливає наслідок:
Наслідок. Якщо зафіксувати  -розбиття множини
-розбиття множини  , тоді існує
, тоді існує

аналогічно, якщо зафіксувати  -розбиття множини
-розбиття множини  , тоді існує
, тоді існує

 .
.
Означення 3.4. Числа 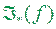 і
і  називають відповідно нижнім і верхнім інтегралом Дарбу функції
називають відповідно нижнім і верхнім інтегралом Дарбу функції  на квадровній множині
на квадровній множині  :
:
 (3.3)
(3.3)
Теорема 3.3. Якщо функція  обмежена на квадровній множині
обмежена на квадровній множині 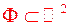 , то
, то
 (3.4)
(3.4)
Доведення.

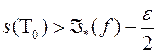 (3.5)
(3.5)
Оскільки множини 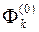 квадровні, то за теоремою 1.7 їхні межі
квадровні, то за теоремою 1.7 їхні межі  також квадровні і мають площу 0:
також квадровні і мають площу 0:
 .
.
Позначимо  , тоді:
, тоді:
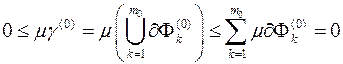 , звідки
, звідки 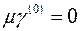 . Тому множину
. Тому множину  , згідно теореми 1.8, можна покрити скінченною системою прямокутників
, згідно теореми 1.8, можна покрити скінченною системою прямокутників  , сума площ яких була б меншою від числа
, сума площ яких була б меншою від числа 
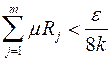 ,
,
а систему  можна покрити іншою системою прямокутників
можна покрити іншою системою прямокутників  таких, щоб система
таких, щоб система 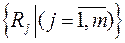 містилась сторого всередині системи
містилась сторого всередині системи 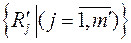

Тоді відстань  між межами множин
між межами множин 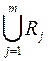 і
і 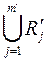 буде деяким додатнім числом.
буде деяким додатнім числом.
Нехай 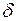 - деяке фіксоване число, причому
- деяке фіксоване число, причому  . Візьмемо довільне
. Візьмемо довільне  - розбиття множини
- розбиття множини 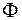 , яке одержується накладанням
, яке одержується накладанням 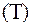 і
і  - розбиттів. Доданки в сумах
- розбиттів. Доданки в сумах  і
і  , які відповідають тим множинам
, які відповідають тим множинам 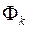 з
з 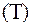 -розбиття, що цілком містяться в якій-небуть множині
-розбиття, що цілком містяться в якій-небуть множині 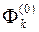 з
з  -розбиття, однакові і в різниці
-розбиття, однакові і в різниці  вони взаємно знищуються. Тому різницю
вони взаємно знищуються. Тому різницю  можна вважати такою, що складається з доданків які відповідають тим множинам
можна вважати такою, що складається з доданків які відповідають тим множинам 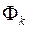 з
з 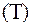 -розбиття, з множиною
-розбиття, з множиною  мають принаймні одну спільну точку. Діаметри цих множин не перевищують числа
мають принаймні одну спільну точку. Діаметри цих множин не перевищують числа 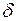 , тому всі ці множини міститимуться у множині
, тому всі ці множини міститимуться у множині 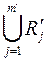 . Отже
. Отже
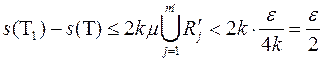
Звідси, використовуючи умову (3.5), маємо:
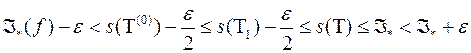
або  .
.
Аналогічно доводять другу рівність 3 (3.4). ▄
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1107; Нарушение авторских прав?; Мы поможем в написании вашей работы!