Властивості подвійних інтегралів

Властивості подвійного інтеграла аналогічні відповідним властивостям визначеного інтеграла.

Властивість 1. Якщо для всіх 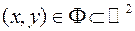, де 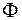- квадровна область, то

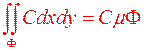
Зокрема

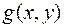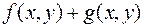Властивість 2. Якщо функції і інтегровні функції на квадровній області , то функції і також інтегровні цій множині, причому

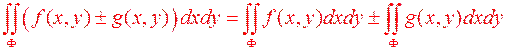
Властивість 3. Якщо функція інтегровна на квадровній множині і , то функція 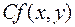теж інтегровна на 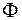, причому

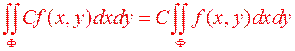
З властивостей 2 і 3 випливає лінійність подвійного інтеграла:

.

Доведіть самостійно властивості 1-4.

Властивість 4. Якщо функції і 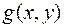інтегровні функції на квадровній області 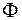, то й добуток цих функцій і частка (при 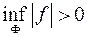) є інтегровна функція на .

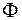Властивість 5.(адитивність інтеграла по множинах). Якщо обмежена функція інтегровна в області 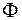і якщо область 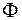кривою 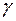площі 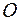розбивається на дві зв’язні без спільних внутрішніх точок області і , то функція інтегровна в кожній області і ,, причому

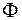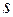Доведення. Нехай . Розіб’ємо області і , на скінченне число квадровних областей, отже ми отримаємо деяке розбиття області . Позначимо через і , і , і 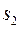верхні і нижні суми Дарбу функції відповідно в областях , і .

Оскільки 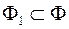і , то з властивостей точної верхньої і точної нижньої меж матимемо нерівності

і

Оскільки функція інтегровна на множині 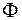, то за критерієм Дарбу (теорема 2.3) випливає, що

,

значить 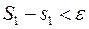і , тобто функція інтегровна в кожній області і .

Якщо у правильних рівностях

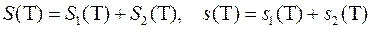
перейти до границі при 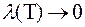, то і отримаємо рівність (3.6) ▄

Зауваження 1.Має місце і обернене твердження: якщо функція обмежена і інтегровна в кожній із квадровних областей і ,, то вона інтегровна в області і має місце рівність (3.6).

Зауваження 2. У зауваженні 1 суттєвим є припущення про те, що обмежена функція.

Дійсно, якщо не враховувати обмеженості функції на і , то можна отримати неправильний висновок. Для цього розглянемо дві множини простору :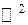

і

і функцію

Функція інтегровна на множині , оскільки вона стала і інтегровна на , оскільки (теорема 3.1). Множина задовольняє умову 1 і разом з тим функція стає необмеженою на цій множині, отже, вона не може бути інтегровною.

Зауваження 3. Якщо функція обмежена і інтегровна на на квадровній множині і обмежена на 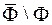, то функція буде інтегровною на замкненій множині 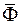, причому

Дійсно, якщо множина 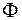квадровна, то й множина 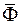квадровна і їхні міри співпадають:

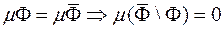
Отже, за властивістю адитивності:

▄

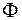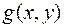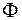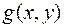Властивість 6. Якщо обмежена, інтегровна функція на множині , і - обмежена функція на , причому , функція інтегровна на множині 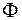і правильна рівність

Доведення. Множина 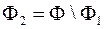квадровна як різниця двох квадровних множин і

Тому, за властивістю адитивності

▄

Властивість 7. Якщо функції і 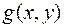інтегровні функції на множині і виконується нерівність , то

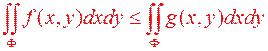
Наслідок. Якщо 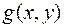, то в умовах властивості 7

Якщо же множина відкрита і для , то

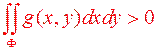
Властивість 8. Якщо обмежена інтегровна функція на множині , то функція 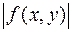також інтегровна на , причому

Властивість 9. (теорема про середнє) Нехай функції і 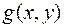обмежені і нтегровні на множині . Якщо і функція 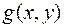не змінює знак, то існує таке числ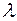о , , що

.

Наслідок. Нехай -замкнена зв’язна квадровна множина, а неперервна функція на цій множині, то існує точка 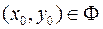така, що

Властивості 7-9 доводяться аналогічно, як і для визначеного інтеграла. Доведіть їх!

Приклад 3.

Користуючись теоремою про середнє, оцінити інтеграл

Розв’язання

Рис. 3.3

Функція визначена і неперервна у замкненій обмеженій області , тому за наслідком властивості 9 існує точка 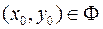така, що

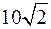Площа квадрата (рис.3.3) із стороною дорівнює 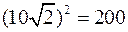, отже

.

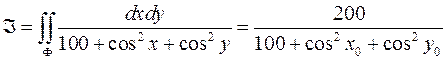Найбільше значення правої частини досягається, якщо знаменник найменший, а це можливо, якщо невід’ємний вираз 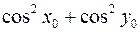дорівнює нулю

.

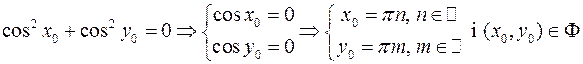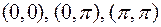Тоді точки в області є, наприклад і т.д. Найменше значення правої частини досягається, якщо знаменник найбільший, а це можливо, якщо

.

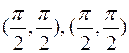Тоді точки в області також є, наприклад і т.д.

Отже, отримаємо оцінку для подвійного інтеграла

,

або

.

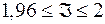Приклад 4

Оцінити інтеграл , .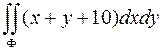

Розв’язання

Як і в попередньому випадку, використаємо теорему про середнє для неперервної функції у замкненій області :

.

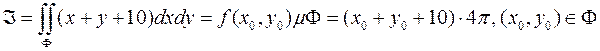Знайдемо найменше і найбільше значення функції у замкненій області , використавши відоме правило з ДЧФБЗ.

І. Знайдемо стаціонарні точки, розв’язавши систему рівнянь

.

У нашому випадку і , тому найменше і найбільше значення функції досягається на межі області.

ІІ. Оцінимо функцію на межі: .

1) 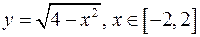(верхнє півколо).

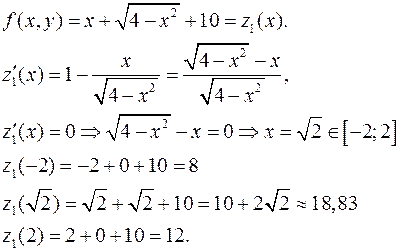
2) (нижнє півколо)

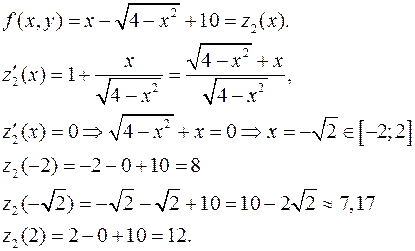
Найбільше і найменше число вибираємо з чисел .

Отже,

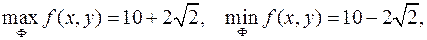
а подвійний інтеграл оцінюється так:

▄

Дата добавления: 2014-11-29