Задачи, связанные с взаимным расположением прямых

Рассмотрим некоторые задачи аналитической геометрии, которые связаны с взаимным расположением прямых в пространстве.

ЗАДАЧА 2. Найти угол между пересекающимися (скрещивающимися) прямыми в пространстве.

ОПРЕДЕЛЕНИЕ. Углом между двумя скрещивающимися прямыми и называется угол между прямой и проекцией прямой на любую плоскость, проходящую через прямую .

Иначе говоря, угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, параллельными данным.

Пусть даны две пересекающиеся или скрещивающиеся прямые:

: и : .

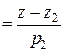Обозначим , 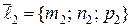– направляющие векторы первой и второй прямой соответственно.

Так как один из углов между прямыми равен углу между их направляющими векторами, а второй угол , то углы и могут быть найдены по формуле

,

или ,

где знак плюс берется в том случае, когда надо найти величину острого угла, а знак минус – когда надо найти величину тупого угла.

ЗАДАЧА 3. Найти расстояние от точки до прямой в пространстве.

Пусть дана прямая

:

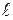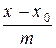
и 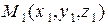– точка, не принадлежащая этой прямой. Обозначим 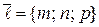– направляющий вектор прямой , – точка на прямой , – расстояние от точки до .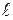

Рассмотрим параллелограмм, построенный на векторах 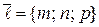и . Тогда – высота этого параллелограмма, опущенная из вершины . Следовательно,

.

ПРИМЕР. Найти расстояние от точки до прямой : .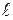

Из условия задачи имеем: , . Тогда

,

,

, ,

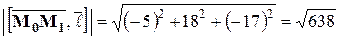– искомое расстояние.

ЗАДАЧА 4. Найти расстояние между скрещивающимися прямыми.

ОПРЕДЕЛЕНИЕ. Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.

Пусть даны две скрещивающиеся прямые

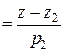: и : ,

и – расстояние между и .

Построим плоскость , проходящую через прямую параллельно . Тогда – расстояние от прямой до плоскости . Найти это расстояние можно по формуле:

,

где – общее уравнение плоскости ,

– любая точка на прямой .

ПРИМЕР. Найти расстояние между двумя прямыми

: и : .

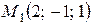1) Прежде всего, установим взаимное расположение данных прямых. По условию задачи: и – направляющий вектор и фиксированная точка первой прямой, и – направляющий вектор и фиксированная точка второй прямой; . Имеем:

1) ∦ – прямые не параллельны;

2) вычислим :

.

Следовательно, данные прямые являются скрещивающимися.

2) Запишем уравнение плоскости , проходящей через прямую параллельно :

: .

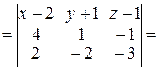
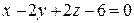Тогда – расстояние от точки до плоскости :

.

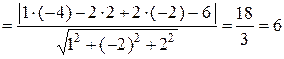Замечание. Предложенный способ нахождения расстояния между скрещивающимися прямыми – не единственный. Можно найти это расстояние, используя векторную алгебру.

Действительно, построим на векторах , и 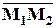пирамиду.

Тогда – высота пирамиды, опущенная из точки и, следовательно,

ЗАДАЧА 5. Найти точку пересечения прямых.

Пусть даны две пересекающиеся прямые

: и : ,

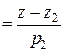– точка пересечения прямых. Тогда – решение системы уравнений

или, переходя к параметрическим уравнениям прямой,

ПРИМЕР. Найти точку пересечения прямых

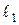: и : .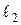

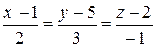1) Прямые и не являются параллельными (их направляющие векторы не коллинеарны) и для них выполняется условие (9):

.

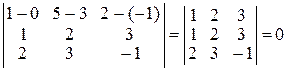Следовательно, прямые 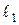и 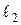– пересекаются.

2) Найдем точку пересечения прямых. Для этого перейдем к их параметрическим уравнениям:

: и :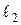

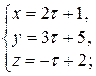
и решим систему

, ;

, , .

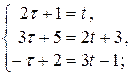
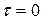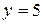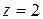Таким образом, точкой пересечения прямых является точка

Дата добавления: 2014-11-29