Учимся решать экономические задачи. Условие максимизации прибыли

Условие максимизации прибыли.

Маржинальный, или предельный, анализ предполагает принятие решения о том, стоит ли производить дополнительную единицу продукции. При наилучшем соотношении выгод и издержек предельный доход должен быть равен предельным издержкам. Следовательно, максимум прибыли достигается при условии:

MR = MC.

Характеристики условия максимизации прибыли:

· До тех пор пока с ростом объёма выпуска выполняется неравенство MR > MC, для увеличения массы прибыли следует наращивать производство. При условии равенства MR = MC можно выбирать любое количество выпуска продукции, которое обеспечивает данное равенство. В данном конкретном случае будет достигаться локальный максимум.

· Данное равенство MR=MC задаёт необходимое, но недостаточное условие максимума прибыли, т.е. оно позволяет найти локальный максимум, но не гарантирует, что данный объём продукции задает глобальный максимум.

· При данном условии MR = MC максимизируется масса прибыли, а не её норма.

Типы задач:

· Задачи на выведение формул всех видов издержек, используемых в экономической теории;

· Задачи на взаимосвязь общих, средних, предельных издержек;

· Задачи на расчёт выручки от продаж;

· Задачи на расчёт амортизационных отчислений.

· Задачи на определение эффекта масштаба производства.

4.1. Допустим, общие издержки фирмы на выпуск Q единиц продукции составляют: TC = 2Q² + 10Q + 162.

А) Выведите функции всех видов издержек, используемых в экономической теории для описания поведения фирмы;

Б) При каких значениях Q средние общие издержки достигают своего минимума?

Решение:

А)

· FC = 162, постоянные издержки;

· VC = 2Q² + 10Q, переменные издержки;

· AFC = FC / Q = 162 / Q, средние постоянные издержки;

· AVC = VC / Q = 2Q + 10, средние переменные издержи;

· ATC = TC / Q = (FC / Q + VC / Q) = (2Q + 10) + 162 / Q, средние общие издержки;

· MC = dTC / dQ = 4Q + 10, предельные издержки.

Б) Минимум средних общих издержек приходится на пересечение графиков AТC с MC, следовательно, мы приравняем эти функции:

2Q + 10 + 162 / Q = 4Q + 10;

2Q² + 10Q + 162 = 4Q² + 10Q;

- 2Q² = - 162;

Q = 9.

Min ATC достигается при выпуске (Q) = 9; при данном объёме производства достигнут производственный оптимум.

4.2. Функция общих издержек имеет вид:

TC = 36 + 12Q + Q². Определить, чему равны средние постоянные издержки при объёме производства, равном 10.

Решение:

AFC = FC / Q где FC = 36, т.к. постоянные издержки не зависят от объёма производимой продукции.

Следовательно: AFC = 36/10 = 3,6.

Ответ: 3,6.

4.3. Определите максимальную выручку, если спрос вплоть до пересечения с осями описывается линейной функцией: Q(D) = b – aР, где Р – цена товара, выпускаемого предпринимателем; b и a – коэффициенты функции спроса.

Решение:

Первый вариант:

а) Согласно экономической теории, предприниматель достигает максимума выручки (дохода) при продаже товара:

· по цене, равной половине запретительной цены (А/2);

· при объёме продаж, равном половине массы насыщения (В/2) (см. рис. 4.5).

Формула максимальной выручки имеет следующий вид:

TR max = A/2 × B/2.

б) Найдём значения запретительной цены и массы насыщения:

· при Q(D) = 0 значение цены P = А = b/a (величина запретительной цены);

· при P = 0 значение Q(D) = В = b (величина массы насыщения).

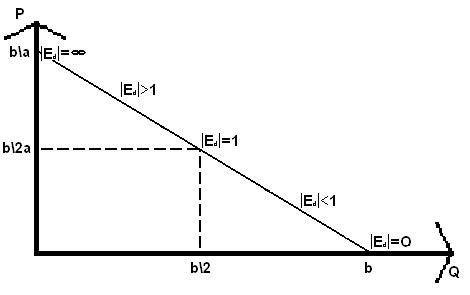
Рис. 4.5. График линейной функции спроса Q(D) = b – a Р.

в) Тогда:

· A/2 = (b/a):2 = b/2a;

· B/2 = b/2;

г) Отсюда значение максимума выручки составит:

TR = b/2a × b/2 = b²/4a.

Второй вариант:

По условию задачи величина спроса составляет: Q(D) = b – aP. Определим цену, при которой предприниматель получает максимальную выручку: TR = P × Q = P × (b – aP).

а) Для этого производную по цене функции выручки приравняем к нулю: (P × (b – aP))’ = 0. Мы получим цену: P = b / 2a.

б) Определим объём производства, при котором предприниматель получит максимум выручки. Подставим значение цены в функцию спроса: Q(D) = b – a × b / 2a = b / 2; ==> Q(D) = b / 2.

в) Следовательно, максимальная выручка предпринимателя составит: TRmax = Q × P = b / 2 × b / 2a = b² / 4a.

Ответ: b²/4a.

4.4. Объём выпуска фирмы в условиях совершенной конкуренции –1000 ед. продукции, цена продукции – 80 у.е., общие средние издержки (АТС) при выпуске 1000 ед. товара - 30. Определите величину бухгалтерской прибыли.

Решение:

а) бухгалтерскую прибыль рассчитаем по формуле: PR = TR – TC. Тогда выручка фирмы составит TR = 80 × 1000 = 80 000.

б) Используя формулу средних общих издержек:

· вычислим величину общих издержек по формуле: AC = TC / Q и

· выразим общие издержки: 30 = ТС / 1000; ТС = 30 000.

в) Тогда прибыль PR = 80 000 – 30 000 = 50 000

Ответ: 50 000.

4.5. Грузовик стоимостью 100 тыс. руб. пройдёт до списания 250 тыс. км. Чему равна величина амортизационных отчислений?

Решение:

Амортизация – это уменьшение бухгалтерской стоимости капитальных ресурсов и постепенное перенесение их стоимости на стоимость произведенного продукта по мере износа.

Существуют различные способы начисления амортизации:

· прямолинейный способ,

· ускоренный способ,

· способ единицы услуг.

Воспользуемся способом единицы услуг т.к. физический нормативный износ связан с оказанием услуг. Следовательно, амортизационные отчисления на 1км составят 0,4 р. независимо от срока службы.

Ответ: 0,4 р. на 1км.

4.6. Даны функции спроса Q(D) = 220 – 4Р и предельных издержек MC = 10 + 4Q. Максимальная прибыль составляет 125 денежных единиц. Определите величину постоянных издержек.

Решение:

Чтобы определить величину постоянных издержек, выведим уравнение функции общих издержек: TC = FC + VC. Дляэтого найдем первообразную функции предельных издержек MC = 10 + 4Q. Уравнение функции общих издержек примет вид: TC = 10Q + 2 Q² + FС.

1. Определим объем производства, максимизирующий прибыль, применив правило максимизации прибыли MC = MR.

2. Выведим уравнение функции предельного дохода. Если применить формулу предельного дохода: MR = (TR)' = (Р × Q)', то мы получим,что MR = ((55 – 0,25Q) × Q)' (где Р = 55 – 0,25Q является обратной функцией для функции спроса Q(D) = 220 – 4Р).Отсюда уравнение функции предельного дохода будет следующим: MR = 55 – 0,5Q. Следовательно, объем производства Qopt, максимизирующий прибыль, составит 10единиц.

3. Вычислим значение общей выручки TR (Qopt 10) = 55Q – 0,25Q² = 525.

4. Найдем значение общих издержек, используя формулу прибыли:

PR = TR – TC,

где

PR = 125, а TR = 525. Величина общих издержек TC составит 400.

Приравняем уравнение функции общих издержек с величиной общих издержек: 400 = 10Q + 2 Q² + FC, где Qopt= 10.

Следовательно, FC= 100.

Ответ: FC = 100.

Дата добавления: 2014-11-29