Теоретический материал. Конкуренция – это экономическая борьба, соперничество за рынок сбыта, за сферу вложения капитала

Конкуренция – это экономическая борьба, соперничество за рынок сбыта, за сферу вложения капитала.

Методы конкуренции бывают: ценовые и неценовые.

Рыночная власть – это способность продавца или покупателя влиять на цену продукции и объём продаж.

Коэффициент Лернера (L), отражающий рыночную власть:

(P – MC) / P = |1 / Ed|.

Различают два вида конкуренции: совершенную и несовершенную.

Рассмотрим рынок совершенной конкуренции на конкретном примере. Цена единицы продукции задана и равна 4 д.е. Данные об объёме выпуска продукции фирмы и издержках производства приведены в таблице:

Количество единиц продукции Q, шт.	Общие издержки TC	Постоянные издержки FC	Переменные издержки VC

1. Рассчитаем значения всех видов издержек производства фирмы, используемых в экономической теории для описания ее поведения.

2. Начертим график, отражающий поведение фирмы на рынке совершенной конкуренции.

3. На основе рассчетов и графика, обоснуем:

а) характерные черты фирмы на рынке совершенной конкуренции,

б) стратегию фирмы на данном рынке.

Решение:

1. Рассчетные значения всех видов издержек, используемых в экономической теории для описания поведения фирмы, сведем в следующую таблицу:

Q	TR	FC	VC	TC	AFC	AVC	ATC	AR	MC	MR	PR
	-				-	-	-	-	-	-	- 150
											- 150
						2,66	12,66				- 130
						2,0	7,0		1,33		- 90
						1,6	4,6				- 30
						1,33	3,33		0,8
					1,58	1,26	2,84
					1,36	1,27	2,64		1,33
					1,25	1,33	2,58
					1,20	1,44	2,64
					1,20	1,6	2,8		-	-

2. На основе данных рассчетов начертим график, отражающий поведение фирмы на рынке совершенной конкуренции (рис.5.1).

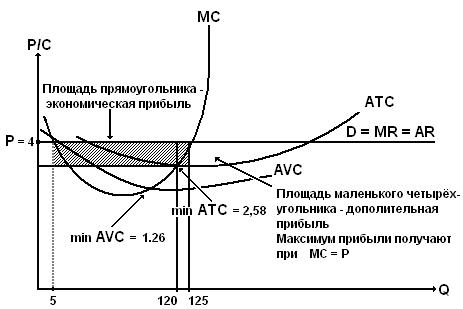
Рис. 5.1. Фирма на рынке совершенной конкуренции.

3. а) Характерные черты фирмы на рынке совершенной конкуренции.

· Период производства кратковременный, поскольку именно он характеризуется невозможностью изменения постоянных издержек (величина FC = 150 д.е. неизменна при любом объме выпуска продукции).

· Фирма – ценополучатель ( цена единицы продукции задана и равна 4 д.е.)

· Коэффициент Лернера ((P – MC) / P = |1 / Ed|) равен нулю, данная рыночная структура не имеет рыночной власти.

· Предельный и средний доходы при любом объеме производства величины постоянные и равны цене:

P = 4 = MR = AR.

· Согласно закону спроса: чем выше цена, тем ниже спрос или наоборот. Однако спрос на данном рынке является совершенно (абсолютно) эластичным. D = MR = AR. Поэтому линия спроса на продукцию фирмы данного рыночного пространства горизонтальна и совпадает с линией предельного и среднего дохода.

б) Стратегия фирмы на рынке совершенной конкуренции.

Для определения объёма производства, максимизирующего прибыль, воспользуемся правилом максимизации прибыли:

MC = MR = Р.

Правило максимизации прибыли выдерживается при объёме выпуска продукции: Q = 5 и Q = 125 единиц. При Q = 5 фирма несёт убытки равные 150 д.е., а при Q = 125 ед. прибыль фирмы максимальная (PR = 170 д.е.). Следовательно, оптимальным объёмом производства будет Q = 125 единиц. При данном выпуске продукции MC = P = 4 = MR = AR.

· Условие максимума прибыли для фирмы рынка совершенной конкуренции будет выглядеть следующим образом:

MC = P = MR = AR.

Несмотря на то, что в интервале от Q= 5 ед. продукции до Q = 75 ед. фирма несёт убытки, ей не стоит уходить с рынка. В случае ухода с рынка убытки фирмы будут равны расходам, связанным с приобретением постоянных факторов производства (FC = 150 д.е.) Если фирма останется в отрасли, то убытки будут меньше на величину постоянных издержек: (FC + VC – PQ) < FC(при этом AVC < P, а VC < PQ). Отсюда стратегия конкурентой фирмы в кратковременном периоде должна состоять в следующем:

· фирма продолжает производство, если min AVC ≤ P < min ATC. В экономической теории такая ситуация называется минимизирующей убытки фирмы.

· AVC ≥ P, то фирме стоит уйти с рынка, т.к. каждая выпускаемая единица продукции приносит дополнительные убытки.

· При увеличении производства продукции с 75 единиц фирма получает экономическую прибыль т.к. AТC < P.

Общетеоретические выводы:

· Линия предложения в кратковременном периоде совпадает с линией предельных издержек на отрезке: minAVC ≤ P < minATC.

· Линия предложения в долговременном периоде совпадает с линией предельных издержек, начиная с выпуска продукции, при котором цена P ≥ min AТC. Экономическая прибыль фирмы в долговременном периоде равна нулю, если выдерживается условие:

MR = AR = MC = AC = P.

Причиной этого является тот факт, что в данном периоде возможен перелив капитала из менее прибыльных отраслей в более прибыльные. Перелив капитала способствует увеличению предложения продукции отрасли и соответственно снижению равновесной цены при неизменном рыночном спросе. Тогда новая цена будет равна величине средних общих и предельных издержек традиционной фирмы: P = AC = MC.

Чистая монополия – единственный производитель уникального продукта (рис. 5.2).

5.2. Чистая монополия.

Характерные черты чистой монополии:

· Монополист обладает рыночной властью. Коэффициент Лернера ((P – MC) / P = |1 / Ed|) больше нуля.

· Производство продукции фирмы – монополиста ограничено рыночным спросом (D = AR).

· Цена на продукцию фирмы – монополиста выше, чем половина запретительной цены (А/2).

· Объем производства продукции ниже, чем половина массы насыщения (В/2).

· Правило максимизации прибыли предполагает равенство MCиMR. Монопольная прибыль определяется разницей между TR и TC.

Рассмотрим поведение фирмы – монополиста на следующем примере. Даны функция издержек производства фирмы – монополиста и функции спроса на продукцию этой монополии на двух рынках:

TC = ¼ Q² + 10Q + 300;

Q(1) = 400 – 2P(1);

Q(2) = 600 – 4P(2).

А) Найдём объёмы продаж и цены на каждом из двух рынков, максимизирующие прибыль, при условии, что ценовая дискриминация незапрещена государством?

Б) Определим прибыль монополиста при ценовой дискриминации.

В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?

Рассуждения:

Из курса экономической теории мы знаем, что монополист, может производить любой объем продук­ции и продавать ее по цене, какой захочет. Главная цель монополиста – получить максимум прибыли при имеющихся возможностях.

Ценовая дискриминация – это продажа товара разным покупателям по разным ценам. Согласно закону спросу: чем выше цена, тем меньше реализуемый объем производства, или наоборот. Между тем от монополиста не зависит существующий на рынке спрос и уровень его издержек в данный момент времени.

Попробуем найти тот объем производства и соот­ветственно уровень цен на каждом из двух рынков, максимизирующие прибыль монополи­ста при условии, что ценовая дискриминация незапрещена государством.

Решение:

А) Воспользуемся правило м максимизации прибыли монополиста при ценовой дискриминации:

MC = MR(1) =MR(2),

где 1, 2 – число разных групп покупателей, приобретающих монопольный товар по разным ценам.

Данное правило основано на принципе выравнивания предельных доходов, получаемых на каждом из двух рынков. Поскольку достигнутый при этом уровень доходов может быть выше или ниже предельных издержек, то для получения наибольшей массы прибыли необходимо или сокращать объём выпуска, или наращивать.

Первая производная общих издержек есть предельные издержки:

(TC)’ = MC = ½Q + 10.

Поскольку монополист функционирует на двух рынках, то функция предельных издержек примет следующий вид:

MC = ½ (Q(1) + Q(2)) + 10.

Выведим функции предельного дохода (MR(1) и MR(2)) монополиста на двух рынках. Функция предельного дохода есть первая производная общего дохода: MR =(TR)’ = (P × Q)’.

Поскольку спрос на первом рынке составляет Q(1) = 400 – 2P(1), а спрос на втором рынке равен Q(2) = 600 – 4P(2), то обратные функции спроса, отражающие зависимость цены спроса от величины спроса соответственно примут соответствующий вид:

P(1) = 200 – ½ Q(1) и

P(2) = 150 – ¼ Q(2).

Отсюда функции предельного дохода на двух рынках составят:

MR(1) =(TR)’ =((200 – ½ Q) × Q)’ = (200Q – ½ Q²)’ = 200 – Q(1);

MR(2) =(TR)’ =((150 – ¼ Q) × Q)’ = (150Q – ¼ Q²)’ = 150 – ½Q(2).

Составим и решим систему уравнений:

Решим выражение(2) и подставим в первое (1). Получим:

Q(2) = 2 Q(1) – 100.

Подставляем Q(2) в первое выражение и находим Q(1):

½ (Q(1) + 2Q(1) – 100) + 10 = 200 – Q(1).

Следовательно, объем производства на каждом из двух рынков, максимизирующие прибыль монополи­ста составят:

· Q(1) = 96 штук;

· Q(2) = 92 штук.

Вычислим уровень цен на каждом из двух рынков, максимизирующий прибыль монополи­ста:

· P(1) = 200 – ½ × 96 = 152 д.е.

· P(2) = 150 – ¼ × 92 = 127 д.е.

Б) Подсчитаем прибыль монополиста при ценовой дискриминации по формуле: PR = TR – TC.

· TR = (Q(1) × P(1) + Q(2) × P(2)) =(96 × 152 + 92 × 127) = 26 276 д.е.

· TC = ¼ (Q(1) + Q(2))² + 10(Q(1) + Q(2)) + 300 = (¼ × 188² + 10 × 188 + 300) = 11 016 д.е.

· PR = 15 260 д.е.

В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?

Во всех экономически развитых странах существует антимонополь­ное законодательство. Данные законы объявляют незаконными действия лиц, которые осуществляют дискриминацию в ценах между различными покупателями товаров одного и того же сорта, качества, когда результатами такой дискриминации является существенное ограничение конкуренции. Данный закон не налагает уголовной ответственности (т.е. является актом гражданского кодекса).

Если ценовая дискриминация будет запрещена государством, то товар на обоих рынках будет продаваться по одной и той же цене. Отсюда общий рыночный спрос составит:

Q(D) = (400 – 2P(1)) + (600 – 4P(2))= 1 000 – 6P.

Тогда обратная функция спроса примет следующий вид:

P = 167 – 1/6Q.

Определим объём производства, максимизирующий прибыль. Найдём Q, исходя из условия максимизации прибыли MC = MR.

MC = ½Q + 10; а

MR = (TR)’ = ((167 - 1/6 Q) × Q)’ = (167 Q – 1/6 Q²)’ = 167 – 1/3 Q.

Приравняем значения MC и MR:

0,5Q + 10 = 167 – 1/3Q.

Следовательно, Q ≈ 188 шт., а Р ≈ 167 – 1/6 × 188 ≈ 136 д.е.

Найдем максимальное значение прибыли: PR = TR – TC.

PR = 188 × 136 – (¼ × 188² + 10 × 188 + 300) = 14 552 д.е.

Прирост прибыли монополиста при ценовой дискриминации составил: 708 д.е. (15260 – 14552).

Дата добавления: 2014-11-29