
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обработка информации о надежности
|
|
|
|
Система сбора информации о надежности
Методы статистического анализа состояния изделий, средства и методы контроля
Без информации о надежности невозможно определить ее показатели, выявить недостатки в конструкции, производстве и ремонте, установить влияние на надежность условий эксплуатации, определить эффективность внедрения мероприятий и на основании всех этих данных принять меры для дальнейшего повышения надежности изделия.
В ходе разработки конструкции такая информация поступает из лабораторий конструкторского отдела, где проводятся стендовые испытания опытных образцов, а также с заводов, полигонов и предприятий, где двигатели проходят опытную эксплуатацию на автомобилях. Поступающая в ходе этих испытаний информация очень важна, так как обычно число испытываемых образцов ограничено, и каждый отказ и неисправность должны быть внимательно изучены и учтены.
После начала промышленного выпуска двигателей организуется сбор информации из эксплуатирующих организаций и от владельцев машин. Для того чтобы информация давала основания для принятия решений, она должна быть достоверной, полной и однородной
Достоверной, т.е. истинной, правильной, отражающей объективные факты без домыслов и догадок.
Полной, т.е. исчерпывающей, содержащей все существенные сведения, которые учитываются во время принятия решений.
Однородной, т.е. относящейся к одинаковым изделиям (деталям, агрегатам), эксплуатирующимся примерно в одинаковых условиях.
Основным источником информации о надежности автомобилей и двигателей является подконтрольная эксплуатация, в ходе которой фиксируются данные об отказах Полученные данные направляются на завод-изготовитель или на ремонтный завод в виде "донесений об отказе изделия". Донесение, если оно правильно заполнено, содержит всю необходимую информацию об изделии, условиях его эксплуатации, характере и причинах отказа, трудоемкости восстановления.
На основании донесений составляются сводные перечни видов отказов изделий, оценок показателей надежности, сводная ведомость расхода запасных частей и другие документы.
Определение показателей надежности производится путем обработки статистической информации, полученной в результате испытаний.
У двигателей одинаковой модели, работающих в примерно одинаковых условиях, показатели надежности будут, тем не менее, отличаться друг от друга. Объясняется это влиянием большого числа различных факторов качества изготовления, режимов нагрузки, погоды, квалификации оператора (водителя), качества топливо смазочных материалов, обслуживания и т.д. Все это неизбежно вызывает рассеивание показателей. Таким образом, время, когда наступает отказ, является случайным событием. Известно, однако, что при многократном повторении наступление случайных событий обладает статистической устойчивостью, которая повышается с увеличением числа испытываемых объектов. На этой закономерности и основано определение показателей надежности, которое, как правило, сводится к нахождению их усредненных значений для данной партии. Что касается каждого отдельного изделия, то можно ожидать, что его показатели будут находиться где-то вблизи этих усредненных значений с большей или меньшей точностью.
В первичной документации, где фиксируются результаты наблюдений за надежностью, содержатся данные, в которых трудно усмотреть какой либо порядок, а тем более закономерность. Обработка этих данных начинается с составления таблицы, в которой они размещаются в порядке увеличения наработки.
Величины ti, ni и wi (среднее значение наработки в интервале, число отказов в интервале или вес и частость), упорядоченные по возрастанию наработки, образуют вариационный ряд. Статистическое значение вероятности безотказной работы и отказов, являющихся накопленными частостями, определено по формулам (7) и (8). Статистическое значение плотности распределения наработки до отказа можно подсчитать по формуле (9). Средняя наработка до отказа определяется по формуле (10).
 (7)
(7)
 (8)
(8)
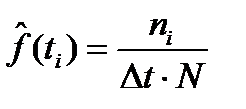 (9)
(9)
 (10)
(10)
Рассеивание результатов оценивают средним арифметическим отклонением q, но чаще дисперсией Д и средним квадратическим отклонением σ.
Каждое-значение наработки отклоняется от среднего на величину ti-tср. Внутри i-интервала таких разностей будет ni. Если найти абсолютную сумму всех отклонений и разделить их на общее число наблюдаемых объектов N, то получится среднее арифметическое отклонение:
 (11)
(11)
Если сложить квадраты всех единичных отклонений, т.е. квадраты разностей ti-tср, и разделить на число наблюдаемых объектов, то получим другую характеристику рассеивания - дисперсию:
 (12)
(12)
Для удобства вычислений обычно используют формулу, которую можно получить из предыдущей
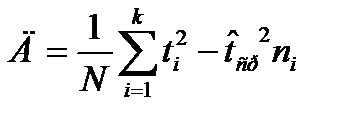 (13)
(13)
Среднее квадратическое отклонение представляет собой взятый с положительным знаком квадратный корень из дисперсии, т.е. σ = √Д.
Если N< 30, то среднее квадратическое отклонение подсчитывается по несколько измененной формуле:
 (14)
(14)
Чтобы оценить, насколько велико рассеивание, подсчитывают коэффициент вариации
V = s/  (15)
(15)
Чем меньше коэффициент вариации, тем плотнее группируются признаки вокруг среднего, тем, следовательно, меньше рассеивание.
Для одинаковых изделий, эксплуатируемых в одинаковых условиях, эти закономерности обнаруживают устойчивость. Поэтому, испытав партию двигателей, т.е. выборку, можно распространить результаты этих испытаний с некоторой точностью на другие двигатели этой же модели, эксплуатируемые в тех же условиях, т.е. на генеральную совокупность, и предсказать их показатели надежности априори, т.е. еще до начала эксплуатации.
Результаты испытаний позволяют найти математическое описание полученных закономерностей, т.е. вывести соответствующие формулы, по которым можно вычислить показатели надежности. Такие формулы принято называть математическими моделями.
Поскольку показатели надежности являются случайными величинами, то их математические модели должны показать, как распределяются показатели надежности в зависимости от наработки. Такими моделями являются законы распределения случайных величин.
Распределение случайной величины - показателя надежности - может быть задано таблицей. В такой таблице представлены результаты наблюдения за группой изделий.
Для получения на основе этой таблицы обобщенных зависимостей, т.е. математических моделей, используются некоторые методы математического анализа.
Наглядным представлением о величине и вариации случайных величин дает их графическое изображение: гистограммы (1, рис.9) и полигоны (2, рис.9) распределения, а также интегральные функции распределения вероятностей отказа (3, рис.9) и безотказной работы (4, рис. 9) и дифференциальные функции или законы распределения случайных величин (рис.10).
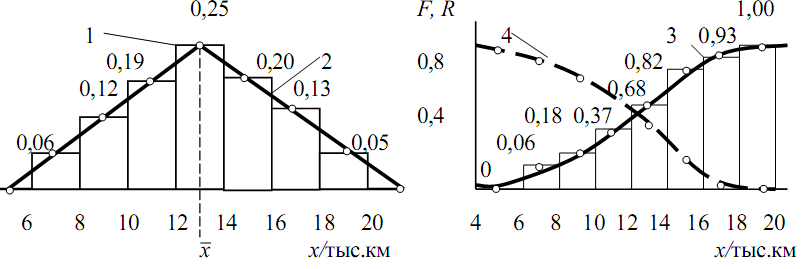
Рис. 9. Графическое изображение случайной величины

Рис. 10. Дифференциальная функция распределения – закон распределения случайных величин
Существует ряд законов распределения случайных величин.
При экспоненциальном законе распределения вероятность появления отказа к моменту наработки может быть определена по формуле (16).
Вероятность того, что к этому моменту отказ не наступит, подсчитывается по формуле (17), плотность вероятности отказа - по формуле (18).
P(t)=e -lt (16)
P(t)=exp [-  ] (17)
] (17)
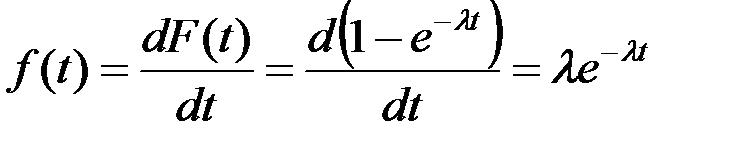 (18)
(18)
Во всех этих формулах е = 2,718 - основание натурального логарифма, λ-интенсивность отказов.
Если отказы исследуемого изделия подчиняются экспоненциальному закону, то для данного изделия в данных условиях эксплуатации λ=const означает, что в равные промежутки наработки число отказавших изделий, приходящихся на каждое оставшееся работоспособным к этому моменту наработки, будет постоянным (рис. 11.).
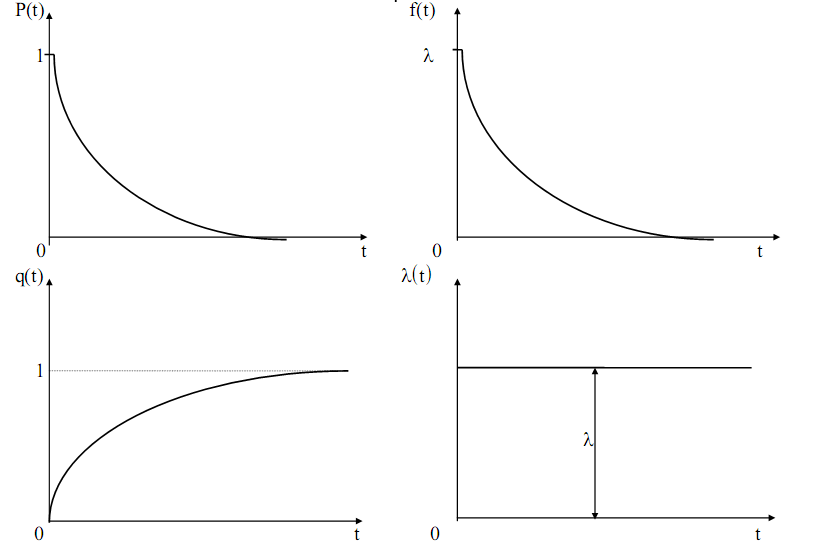
Рис. 11. Количественные характеристики основных законов распределения в зависимости от наработки t
Если отказы изделия подчиняются экспоненциальному закону, то для обеспечения высокой безотказности даже в самый начальный период работы средняя наработка до отказа должна достигать весьма высоких значений.
Обычно по экспоненциальному закону распределяются внезапные отказы. Их интенсивности мало зависят от времени. Что касается постепенных отказов, то λ(t)≠const и экспоненциальный закон здесь обычно неприменим.
Нормальный закон распределения (закон Гаусса) в ряде случаев хорошо согласуется с экспериментальными данными при испытаниях на надежность. Это относится прежде всего к таким процессам, при которых отказы вызываются многими равновлияющими причинами. Этот закон распределения характеризует вероятность отказа при длительном изменении характеристик изделия (старения, износа). Нормальный закон распределения характеризует распределение времени безотказной работы изделия при возникновении отказов из-за износов и старения.
Плотность распределения времени безотказной работы Т изделия равна
 (19)
(19)
где mt, Dt – параметр закона распределения,
mt – среднее значение случайной величины Т,
Dt – дисперсия случайной величины Т.
Имеем
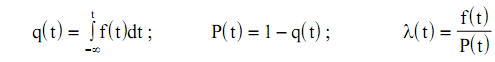
Для нормального закона распределения q (t) примет вид
 (20)
(20)
Для описания времени безотказной работы Т этот закон справедлив, если mt >>σt, где σt =  (рис. 12).
(рис. 12).
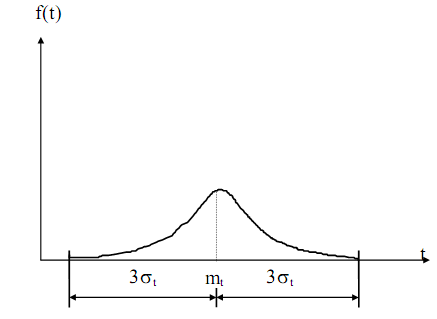
Рис. 12. График нормального закона распределения
Параметрами распределения для нормального закона являются σ и tср.
Расчеты удобно производить, если указанное выражение преобразовать к более простому виду. Это делается таким образом, чтобы начало координат переместить на ось симметрии, т.е. в точку tср, наработку представить в относительных единицах, а именно в частях, пропорциональных среднему квадратическому отклонению. Для этого надо заменить переменную величину t другой:
х = (t-tср)/ σ (21)
а величину среднего квадратического отклонения принять за единицу измерения по оси абсцисс. Тогда в новых координатах получим так называемую центрированную и нормированную функцию, плотность распределения которой
 (22)
(22)
Площадь под кривой φ(x) в пределах - ∞<x < ∞ равна 1.
Интегральная функция
 (23)
(23)
Функция распределения F(x) может быть представлена в виде графика, который строится подобно гистограмме, только высоты прямоугольников равны значениям функции распределения соответствующих интервалов (рис. 13).

Рис. 13. График эмпирической интегральной функции распределения опытных данных
Весьма гибким для оценки показателей надежности является закон Вейбулла. Графически функция P(t) для распределения Вейбулла представлена на рис. 14.
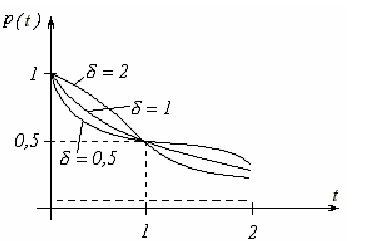
Рис. 14. Функция P(t) для распределения Вейбулла
Для распределения Вейбулла плотность распределения времени безотказной работы Т изделия имеет вид
 , (24)
, (24)
где a и k – параметры закона распределения Вейбулла.
Графически закон распределения Вейбулла изображен на рис. 15.

Рис. 15. Графический вид закона распределения Вейбулла
Параметр a оказывает влияние на форму кривых. Он называется параметром формы. Параметр t0 характеризует растянутость кривых вдоль оси t. Это параметр масштаба. Если a= 1, то P(t) =  Нетрудно видеть, что в этом случае имеет место экспоненциальный закон. Тогда t =tср. При b = 2,5...3,5 распределение Вейбулла близко к нормальному. Этим объясняется гибкость закона Вейбулла и широкое его применение. С его помощью можно приблизиться к моделированию процессов возникновения внезапных отказов, когда параметр близок к единице, и отказов из-за износа, когда распределение становится близким к нормальному, а также тогда, когда совместно действуют причины, вызывающие оба этих отказа.
Нетрудно видеть, что в этом случае имеет место экспоненциальный закон. Тогда t =tср. При b = 2,5...3,5 распределение Вейбулла близко к нормальному. Этим объясняется гибкость закона Вейбулла и широкое его применение. С его помощью можно приблизиться к моделированию процессов возникновения внезапных отказов, когда параметр близок к единице, и отказов из-за износа, когда распределение становится близким к нормальному, а также тогда, когда совместно действуют причины, вызывающие оба этих отказа.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 3057; Нарушение авторских прав?; Мы поможем в написании вашей работы!