Взаимодействие нейтронов с веществом

Лекция 2 Ядерное рассеяние нейтронов

Сечения взаимодействия

Когда нейтрон пролетает вблизи ядра, то возможны следующие взаимодействия:

а). Нейтрон поглощается, т.е. захватывается ядром. Ядро переходит в возбужденное состояние. Возврат в основное состояние сопровождается, как правило, испусканием g-квантов.

б). Нейтрон рассеивается, т.е. изменяется его направление движения и энергия. Это рассеяние может быть как упругим так и неупругим рассеяние нейтронов.

Пусть на образец падает поток нейтронов I ₀ в единицу времени на единицу площади. Примем, что I _s и I _a – число актов рассеяния и поглощения нейтронов в единицу времени в образце, то полное сечение рассеяния s_s и поглощения s_a будут определены как:

I _s = I ₀×s_s

I _a = I ₀×s_a.

Обе величины имеют размеренность площади. Обычно сечение измеряют в барнах.

1 барн = 10^-24 см².

Дифференциальное сечение рассеяния - это сечение d s/ d W, которое задает вероятность того, что в результате рассеяния нейтрон вылетает из образца под определенным углом W в элемент телесного угла d W.

Дважды д ифференциальное сечение рассеяния – это сечение d ²s/ d W d E, которое задает вероятность того, что в результате рассеяния нейтрон вылетает из образца под определенным углом W в элемент телесного угла d W и при этом изменение энергии нейтрона попадет в интервал от ħE до ħ (E + dE).

Очевидно, что

s_s = òd E (ds/d E) = òd E òdW(d²s/dWd E). (2.1)

Следует различать два основных вида рассеяния нейтронов на отдельных атомах:

1) ядерное рассеяние, за которое ответственно поле ядерных сил,

2) магнитное рассеяние, которое определяется электромагнитными силами, возникающими из-за того, что нейтрон, имеющий собственный магнитный момент, взаимодействует с магнитным моментом электронной оболочки атома.

Для ядерных сил потенциал взаимодействия нейтрона с ядром хорошо описывается так называемым потенциалом Ферми:

V(r) = 2p ħ ²/må b _id(r – R _i), (2.2)

где b _i – длина (амплитуда) рассеяния i -ядра, R _i – радиус-вектор положения i -ядра в конденсированном веществе и суммирование проводится по всем ядрам. Псевдопотенциал Ферми является эмпирической функцией и отражает тот факт, что ядерное взаимодействие нейтрона с ядром имеет малый радиус действия. Амплитуда рассеяния есть фундаментальная характеристика взаимодействия нейтрона с ядром, которая зависит от типа изотопа элемента и относительной ориентации спина нейтрона и спина ядра.

Обычно в веществе мы имеем смесь изотопов одного и того же элемента, а также случайный набор относительных ориентаций спинов нейтрона и ядра в процессе рассеяния. Среднее значение < b _i> по всем изотопам и спиновым состояниям системы ядро + нейтрон для определенного элемента называется когерентной длиной рассеяния (амплитудой когерентного рассеяния) для этого элемента: b _i^coh = < b _i>.

Спин ядра с четным (нечетным) числом протонов и нейтронов.

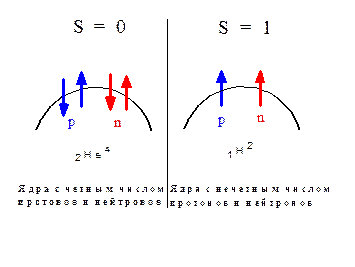
Некогерентной длиной рассеяния (амплитудой некогерентного рассеяния) называется среднеквадратичное отклонение b _i от < b _i>:

b _i^inc = [< b _i²> - < b _i>²]^1/2. (2.3)

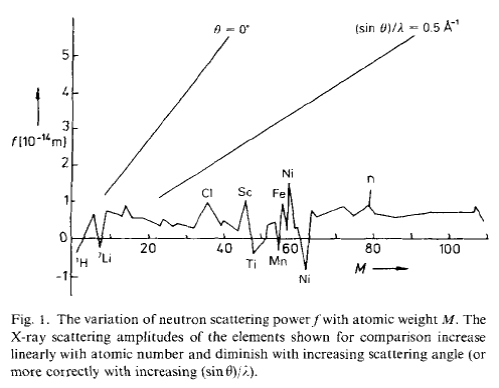
В отличие от рентгеновских лучей амплитуда рассеяния нейтронов зависит от атомного номера элемента нерегулярным образом и для различных изотопов одного и тоже элемента может отличаться даже знаком.

Для примера рассмотрим изотоп некоторого элемента. Пусть он имеет ядерный спин S и взаимодействует с нейтроном со спином ½. Тогда получим две возможных амплитуды рассеяния b ⁺ и b ^- , связанные с двумя возможными значениями полного спина такой системы

S⁺ = S + ½ и S^- = S - ½.

Поскольку имеется

n + = 2S⁺ + 1 и n ^- = 2S^- - 1

состояний соответственно для спинов S⁺ и S^-, то при условии равной вероятности для каждого из таких состояний получим:

< b > = 1/(n ⁺ + n ^-)[ n ⁺ b ⁺ + n ^- b ^-], (2.4)

< b ²> = 1/(n⁺ + n^-)[ n ⁺(b ⁺)² + n ^-(b ^-)²] = 1/(2S + 1)[(S + 1)(b ⁺)² + S(b ^-)²], (2.5)

откуда

b ^inc = 1/(2S + 1)[(S + 1) b ⁺ + S b ^-]. (2.6)

Таким образом, за счет существования двух различных значений полного спина системы ядро + нейтрон в процессе рассеяния появляется дополнительный источник некогерентного рассеяния нейтрона на ядре (спиновая некогерентность).

Приведенные выражения для < b > и < b ²> позволяют ввести понятия сечений когерентного и некогерентного рассеяния.

s_coh = 4p< b >²

s_inc = 4p(< b ²> - < b >²) = 4p<(b - < b >)²>. (2.7)

Полное сечение рассеяния нейтронов ядром будет суммой когерентной и некогерентной компонент:

s_tot = s_coh + s_inc.

Пока мы рассматривали изолированное (свободное) ядро, однако рассеиватель состоит из связанных между собой ядер. Учет это обстоятельства приводит к следующему выражению:

s_своб = [A/(A + 1)]²s_связ, (2.8)

где А –массовое число. С увеличением массы рассеивающего ядра разница между s_своб и s_связ быстро уменьшается. Разница существенна лишь, например, для водорода, для которого s_своб составляет ¼ s_связ. Соответственно амплитуды рассеяния протоном в свободном и связанном состояниях различаются вдвое.

Дата добавления: 2014-11-29